8.2: The Wavefunctions
de oplossingen voor het waterstofatoom Schrödingervergelijking zijn functies die producten zijn van een sferische harmonische functie en een radiale functie.
\
de golffuncties voor het waterstofatoom zijn afhankelijk van de drie variabelen r, \(\theta\) en \(\varphi \) en de drie kwantumnummers n, \(l\) en \(m_l\). De variabelen geven de positie van het elektron ten opzichte van het proton in sferische coördinaten. Het absolute kwadraat van de golffunctie, \(| \psi (r, \theta, \ varphi) / ^2\), geëvalueerd op \(r\), \(\theta\), en \(\varphi\) geeft de waarschijnlijkheidsdichtheid van het vinden van het elektron binnen een differentieel volume \(d \tau\), gecentreerd op de positie gespecificeerd door r, \(\theta\), en \(\varphi\).
oefening \(\Paginindex{1}\)
Wat is de waarde van de integraal
\
De kwantumnummers hebben namen: \(n\) wordt het hoofd kwantumgetal genoemd, \(l\) wordt het hoekmoment kwantumgetal genoemd, en \(m_l\) wordt het magnetische kwantumgetal genoemd omdat(zoals we in Paragraaf 8.4 zullen zien) de energie in een magnetisch veld afhangt van \(m_l\). Vaak wordt \(l\) het azimutale kwantumgetal genoemd omdat het een gevolg is van de \(\theta\)-vergelijking, waarbij de azimutale hoek \(\Theta\) betrokken is, verwijzend naar de hoek met het zenit.
deze kwantumgetallen hebben specifieke waarden die worden bepaald door de fysische beperkingen of randvoorwaarden die worden opgelegd aan de schrödingervergelijking: \(n\) moet een geheel getal groter zijn dan 0, \(l\) kan de waarden 0 tot n‑1 hebben, en \(m_l\) kan \(2l + 1\) waarden hebben variërend van \(- l\) ‑ tot \(+l\) in eenheidsstappen of gehele getallen. De waarden van het kwantumgetal \(l\) worden meestal gecodeerd met een letter: s betekent 0, p betekent 1, d betekent 2, f betekent 3; de volgende codes gaan Alfabetisch verder (bijvoorbeeld g betekent \(l = 4\)). De kwantumgetallen specificeren de kwantisatie van fysische grootheden. De discrete energieën van verschillende toestanden van het waterstofatoom worden gegeven door \(n\), de magnitude van het impulsmoment wordt gegeven door \(l\), en een component van het impulsmoment(meestal gekozen door chemici als de Z‑component) wordt gegeven door \(m_l\). Het totale aantal orbitalen met een bepaalde waarde van \(n\) is \(n^2\).
oefening \(\Pagindex{2}\)
beschouw meerdere waarden voor n, en laat zien dat het aantal orbitalen voor elke n \(n^2\) is.
oefening \(\Pagindex{3}\)
Stel een tabel samen waarin de toegestane waarden voor de kwantumnummers n, \(l\) en \(m_l\) worden samengevat. voor energieniveaus 1 tot en met 7 van waterstof.
oefening \(\Pagindex{4}\)
de notatie 3d specificeert de kwantumnummers voor een elektron in het waterstofatoom. Wat zijn de waarden voor n en \(l\)? Wat zijn de waarden voor de energie en het impulsmoment? Wat zijn de mogelijke waarden voor het magnetische kwantumgetal? Wat zijn de mogelijke oriëntaties voor de impulsmomentvector?
De waterstofatoomgolffuncties \(\psi (r, \ theta, \ varphi)\), worden atomaire orbitalen genoemd. Een atomaire orbitaal is een functie die een elektron in een atoom beschrijft. De golffunctie met n= 1, \(l = 1\), en \(m_l\) = 0 wordt de 1s-orbitaal genoemd, en een elektron dat door deze functie wordt beschreven zou “in” de ls-orbitaal zijn, dat wil zeggen een 1s-orbitale toestand hebben. De beperkingen op \(n\), \(l)\), en \(m_l\) die worden opgelegd tijdens de oplossing van het waterstofatoom Schrödingervergelijking verklaren waarom er een enkele 1s orbitaal is, waarom er drie 2P orbitalen zijn, vijf 3d orbitalen, enz. We zullen zien wanneer we multi-elektron atomen in hoofdstuk 9 beschouwen dat deze beperkingen de kenmerken van het Periodiek Systeem verklaren. Met andere woorden, het Periodiek Systeem is een manifestatie van het Schrödinger-model en de fysieke beperkingen die worden opgelegd om de oplossingen voor de Schrödingervergelijking voor het waterstofatoom te verkrijgen.
het visualiseren van de variatie van een elektronische golffunctie met \(r\), \(\theta\), en \(\varphi\) is belangrijk omdat het absolute kwadraat van de golffunctie de ladingsverdeling (elektronkansdichtheid) in een atoom of molecuul weergeeft. De ladingsverdeling staat centraal in de chemie omdat het gerelateerd is aan chemische reactiviteit. Bijvoorbeeld, wordt een elektronendeficiënt deel van één molecuul aangetrokken tot een elektronenrijk gebied van een andere molecuul, en dergelijke interactie spelen een belangrijke rol in chemische interactie die zich van substitutie en additie reacties tot eiwit het vouwen en de interactie van substraten met enzymen uitstrekken.
het visualiseren van golffuncties en ladingsdistributies is een uitdaging omdat het vereist dat het gedrag van een functie van drie variabelen in de driedimensionale ruimte wordt onderzocht. Deze visualisatie wordt vergemakkelijkt door de radiale en hoekige delen afzonderlijk te bekijken, maar het afzonderlijk plotten van de radiale en hoekige delen geeft de vorm van een orbitaal niet erg goed weer. De vorm kan beter worden onthuld in een kansdichtheid plot. Om zo ‘ n driedimensionale plot te maken, verdeel je de ruimte in kleine volume-elementen, bereken je \(\psi^* \psi \) in het midden van elk volume-element, en schaduw, stippel of kleur dat volume-element in verhouding tot de grootte van \(\psi^* \psi \). Verwar dergelijke plots niet met polaire plots, die er vergelijkbaar uitzien.
Kansdichtheden kunnen ook worden weergegeven door contourafbeeldingen, zoals weergegeven in Figuur \(\Paginindex{1}\).
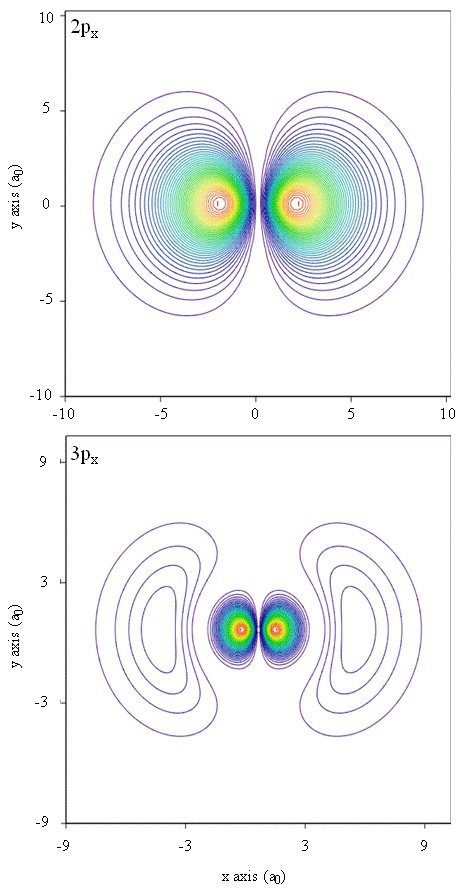
een andere representationele techniek, virtual reality modeling, heeft een grote belofte voor de representatie van elektrondichtheden. Stel je bijvoorbeeld voor dat je elektronendichtheid kunt ervaren als een kracht of weerstand op een toverstaf die je door de driedimensionale ruimte beweegt. Apparaten zoals deze, zogenaamde haptische apparaten, bestaan al en worden gebruikt om wetenschappelijke informatie weer te geven. Zou het ook niet interessant zijn om door een atomaire orbitaal te “vliegen” en veranderingen in elektronendichtheid te ervaren als kleurveranderingen of vertroebelingen? Speciaal ontworpen ruimtes met 3D-schermen en” slimme ” glazen die feedback geven over de richting van de blik van de kijker worden momenteel ontwikkeld om ons in staat te stellen dergelijke sensaties te ervaren.
methoden voor het afzonderlijk onderzoeken van de radiale delen van atomaire orbitalen leveren nuttige informatie op over de verdeling van de ladingsdichtheid binnen de orbitalen. Grafieken van de radiale functies, \(R (r)\), voor de 1s, 2s en 2p orbitalen uitgezet in Figuur \(\Paginindex{2}\).
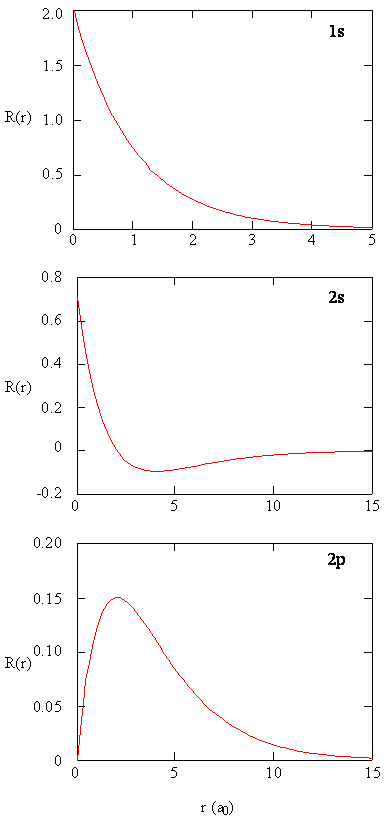
de 1s-functie in Figuur \(\Paginindex{2}\) begint met een hoge positieve waarde aan de kern en vervalt exponentieel tot in wezen nul na 5 Bohr-stralen. De hoge waarde in de kern kan verrassend zijn, maar zoals we later zullen zien, is de kans op het vinden van een elektron in de kern verdwenen klein.
merk vervolgens op hoe de radiale functie voor de 2s-orbitaal, figuur \(\Paginindex{2}\), naar nul gaat en negatief wordt. Dit gedrag onthult de aanwezigheid van een radiale knoop in de functie. Een radiale knoop treedt op wanneer de radiale functie gelijk is aan nul anders dan op \(r = 0\) of \(r = ∞\). Knooppunten en het beperken van gedrag van atomaire orbitale functies zijn beide nuttig bij het identificeren welke orbitaal wordt beschreven door welke golffunctie. Alle s-functies hebben bijvoorbeeld niet-nul golffunctiewaarden op \(r = 0\), maar p, d, f en alle andere functies gaan naar nul bij de oorsprong. Het is handig om te onthouden dat er\ (n-1-l\) radiale knooppunten zijn in een golffunctie, wat betekent dat een 1s-orbitaal geen radiale knooppunten heeft, een 2s één radiale knooppunt, enzovoort.
oefening \(\Paginindex{5}\)
onderzoek de wiskundige vormen van de radiale golffuncties. Welke functie in de functies zorgt ervoor dat sommige van hen naar nul gaan bij de oorsprong, terwijl de S-functies niet naar nul gaan bij de oorsprong?
oefening \(\Paginindex{6}\)
welk wiskundig kenmerk van elk van de radiale functies bepaalt het aantal radiale knooppunten?
oefening \(\Paginindex{7}\)
bij welke waarde van r komt de 2S radiale knoop voor?
oefening \(\Pagindex{8}\)
Maak een tabel die de energie, het aantal radiale knooppunten, en het aantal hoekknooppunten en het totale aantal knooppunten voor elke functie levert met n = 1, 2 en 3. Identificeer de relatie tussen de energie en het aantal knooppunten. Identificeer de relatie tussen het aantal radiale knooppunten en het aantal hoekige knooppunten.
de hoeveelheid \(R(r) ^* R(r)\) geeft de radiale kansdichtheid, d.w.z. de kansdichtheid voor het elektron om zich op een punt te bevinden dat zich op de afstand \(r\) van het proton bevindt. Radiale waarschijnlijkheidsdichtheden voor drie typen atomaire orbitalen worden in Figuur uitgezet (\Paginindex{3}\).
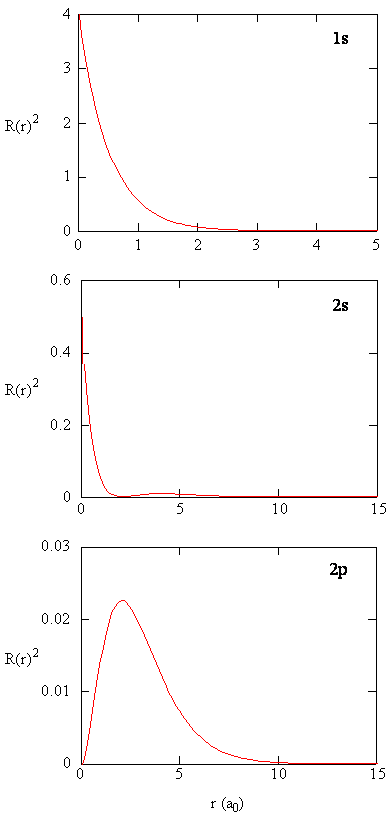
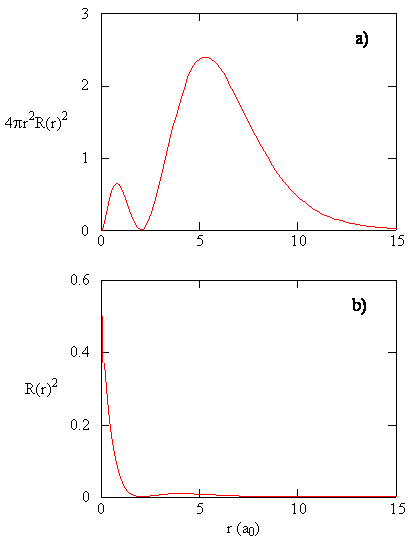
wanneer de radiale waarschijnlijkheidsdichtheid voor elke waarde van r wordt vermenigvuldigd met de oppervlakte van het sferische oppervlak vertegenwoordigd door die specifieke waarde van r, krijgen we de radiale verdelingsfunctie. De radiale verdelingsfunctie geeft de kans dat een elektron ergens op het oppervlak van een bol op een afstand r van het proton wordt gevonden. Omdat het oppervlak van een bolvormig oppervlak \(4 \pi r^2\) is, wordt de radiale verdelingsfunctie gegeven door \(4 \pi r^2 R(r) ^* R(r)\).
radiale distributiefuncties worden weergegeven in Figuur \(\Paginindex{4}\). Bij kleine waarden van r is de radiale verdelingsfunctie laag omdat het kleine oppervlak voor kleine radii de hoge waarde van de radiale waarschijnlijkheidsfunctie nabij de kern moduleert. Als we \(r\) verhogen, neemt het oppervlak geassocieerd met een gegeven waarde van r toe, en de term \(r^2\) zorgt ervoor dat de radiale verdelingsfunctie toeneemt, ook al begint de radiale waarschijnlijkheidsdichtheid af te nemen. Bij grote waarden van \(r\) weegt het exponentiële verval van de radiale functie op tegen de toename veroorzaakt door de \(r^2\) term en neemt de radiale verdelingsfunctie af.
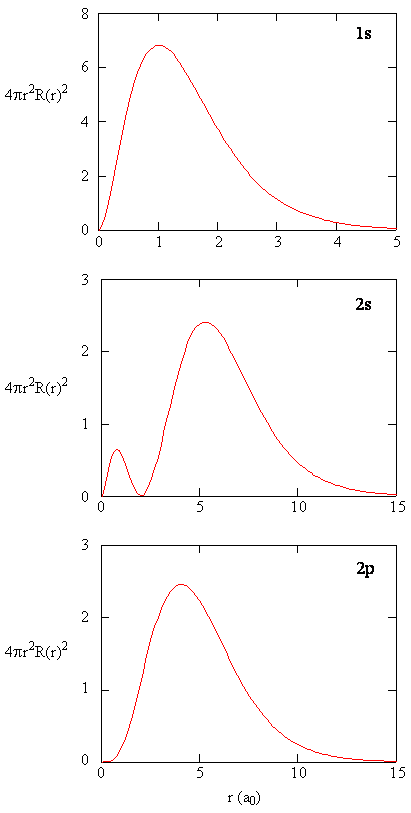
oefening \(\Paginindex{9}\)
Schrijf een kwaliteitsvergelijking van de radiale functie en de radiale distributiefunctie voor de 2s-orbitaal. Zie figuur (\Paginindex{5}\)
bijdragers en Attributies
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (“Quantum States of Atoms and moleculen”)