Antennes stralen elektromagnetische energie uit om informatie te verzenden of te ontvangen. Daarom worden de termen energie en macht geassocieerd met deze elektromagnetische golven en we moeten ze bespreken. Een elektromagnetische golf heeft zowel elektrische als magnetische velden.

beschouw de golf op elk moment, die kan worden bekeken in beide vectoren. De volgende figuur toont de weergave van elektrische en magnetische veldcomponenten in een elektromagnetische golf.

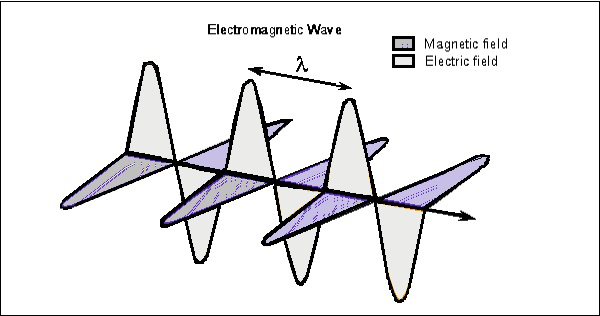
De elektrische golf is verticaal aanwezig ten opzichte van de voortplanting van EM-golf, terwijl de magnetische golf horizontaal is geplaatst. Beide velden staan haaks op elkaar.

Poynteervector

Poynteervector beschrijft de energie van de EM-golf per tijdseenheid per oppervlakte-eenheid op een bepaald moment van de tijd. John Henry Poynting ontleende deze vector voor het eerst in 1884 en werd daarom naar hem vernoemd.

definitie − “Poynteervector geeft de snelheid van energieoverdracht per oppervlakte-eenheid”

of

“De energie die een golf per tijdseenheid per oppervlakte-eenheid draagt, wordt gegeven door de Poynteervector.”

Poynting vector wordt weergegeven Door Ŝ.

eenheden

de SI-eenheid van de Poynteervector is W / m2.

wiskundige uitdrukking

de hoeveelheid die wordt gebruikt om het vermogen van de elektromagnetische golven te beschrijven is de momentane Poynting vector, die wordt gedefinieerd als

$$\hat{S} = \hat{E} \times \hat{H}$$

waarbij

• $\hat{S}$ is de momentane Poynting vector (W/m2).

• $\hat{E}$ is de momentane elektrische veldintensiteit (V / m).

• $\hat{H}$ is de momentane magnetische veldintensiteit (A / m).

het belangrijke punt dat hier moet worden opgemerkt is dat de magnitude van E groter is dan H binnen een EM-golf. Beide dragen echter dezelfde hoeveelheid energie bij. Ŝ is de vector, die zowel richting als magnitude heeft. De richting van Ŝ is gelijk aan de snelheid van de Golf. Zijn grootte hangt af van de E en H.

afleiding van Poynting Vector

om een duidelijk idee te hebben over Poynting vector, laten we de afleiding van deze Poynting vector doorlopen, in een stap-voor-stap proces.

stel je voor dat een EM-golf een gebied (A) passeert loodrecht op de X-as waarlangs de Golf zich verplaatst. Tijdens het passeren van een, in infinitesimale tijd (dt), de Golf reist een afstand (dx).

$$DX = C\ dt$$

waarbij

$$c = velocity\ of\ light = 3\times 10^{8}m/s$$$$$volume, dv = Adx = AC\ dt$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$$= \EPSILON_{0} AC \ E^{2}\ dt$$

overgedragen in tijd (dt) per gebied (a) is −

$$s = \frac{Energy}{time\times area} = \frac{DW}{DT\ a} = \frac{\epsilon_{0}Ace^{2}\ dt}{dt\ a} = \epsilon_{0}C\:E^{2}$$

Sinds

$$\frac{E}{H} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \ dan\ S= \frac{CB^{2}}{\mu_{0}}$$

Sinds

$$C = \frac{E}{H} \ dan \ S = \frac{ES}{\mu_{0}}$$$$= \hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Ŝ geeft de Poynting vector.

De Bovenstaande vergelijking geeft ons de energie per tijdseenheid, per oppervlakte-eenheid op een bepaald moment van de tijd, die wordt genoemd als Poynting vector.