8.2: Wavefunctions
řešení vodíkového atomu Schrödingerova rovnice jsou funkce, které jsou produkty sférické harmonické funkce a radiální funkce.
\
wavefunctions pro atom vodíku závisí na třech proměnných r, \(\theta\) a \(\varphi \) a tři kvantová čísla n, \(l\) a \(m_l\). Proměnné dávají polohu elektronu vzhledem k protonu ve sférických souřadnicích. Absolutní náměstí wavefunction, \(| \psi (r, \theta , \varphi )|^2\) v bodě \(r\), \(\theta \) a \(\varphi\) dává hustoty pravděpodobnosti nalezení elektronu uvnitř diferenciální objem \(d \tau\), střed na pozici zadané r, \(\theta \) a \(\varphi\).
Cvičení \(\PageIndex{1}\)
Jaká je hodnota integrálu
\
kvantová čísla mají jména: \(n\) se nazývá hlavní kvantové číslo, \(l\) je tzv. vedlejší kvantové číslo a \(m_l\) se nazývá magnetické kvantové číslo, protože (jak uvidíme v kapitole 8.4) energie v magnetickém poli závisí na \(m_l\). Často \(l\) se nazývá azimutální kvantové číslo, protože je důsledkem \(\theta\) – rovnice, která zahrnuje azimutální úhel \(\Theta \), odkazující na úhel k zenitu.
tato kvantová čísla mají specifické hodnoty, které jsou diktovány fyzikálními omezeními nebo okrajovými podmínkami uloženými na Schrödingerově rovnici: \(n\) musí být celé číslo větší než 0, \(l\), může mít hodnoty 0 až n‑1, a \(m_l\) může mít \(2l + 1\) hodnot v rozmezí od \(l\) ‑ \(+l\), v oddělení nebo celé kroky. Hodnoty kvantového čísla \(l\) jsou obvykle kódovány písmenem: s znamená 0, p znamená 1, d znamená 2, f znamená 3; další kódy pokračují abecedně (např. G znamená \(l = 4\)). Kvantová čísla určují kvantování fyzikálních veličin. Diskrétní energie různých stavů atomu vodíku jsou dány \(n\), velikost momentu hybnosti je dán tím, že \(l\), a jednu složku momentu hybnosti (obvykle volí chemici být z‑složka) je dán vztahem \(m_l\). Celkový počet orbitalů s určitou hodnotou \(n\) je \(n^2\).
Cvičení \(\PageIndex{2}\)
Zvážit několik hodnot pro n, a ukazují, že počet orbitalů pro každé n je \(n^2\).
Cvičení \(\PageIndex{3}\)
Construct tabulky shrnující přípustné hodnoty pro kvantová čísla n, \(l\) a \(m_l\). pro energetické hladiny 1 až 7 vodíku.
Cvičení \(\PageIndex{4}\)
zápis 3d určuje kvantová čísla elektronu v atomu vodíku. Jaké jsou hodnoty pro n A \(l\) ? Jaké jsou hodnoty energie a momentu hybnosti? Jaké jsou možné hodnoty magnetického kvantového čísla? Jaké jsou možné orientace vektoru momentu hybnosti?
atom vodíku wavefunctions, \(\psi (r, \theta , \varphi )\), se nazývají atomové orbitaly. Atomový orbital je funkce, která popisuje jeden elektron v atomu. Wavefunction s n = 1, \(l=1\) a \(m_l\) = 0, se nazývá orbital 1s, a elektron, který je popsán pomocí této funkce je řekl, aby byl „in“ je orbitální, tj. máme 1s orbital státu. Omezení na \(n\), \(l)\) a \(m_l\), které jsou uloženy v průběhu řešení vodíkového atomu Schrödingerova rovnice vysvětlit, proč tam je jeden orbital 1s, proč tam jsou tři 2p orbitaly, pět 3d orbitaly, atd. Uvidíme, když vezmeme v úvahu atomy více elektronů v kapitole 9, že tato omezení vysvětlují vlastnosti periodické tabulky. Jinými slovy, Periodická Tabulka je projevem Schrödingerova modelu a fyzické omezení, získat řešení Schrödingerovy rovnice pro atom vodíku.
Vizualizace variace elektronický wavefunction s \(r\), \(\theta\) a \(\varphi\) je důležité, protože absolutní náměstí wavefunction znázorňuje rozložení náboje elektronu (hustoty pravděpodobnosti) v atomu nebo molekuly. Distribuce náboje je pro chemii Ústřední, protože souvisí s chemickou reaktivitou. Například elektron deficitní část jedné molekuly je přitahován elektron bohatý region z jiné molekuly, a tyto interakce hrají významnou roli v chemických interakcí v rozmezí od střídání a kromě reakce na skládání bílkovin a interakce substrátů s enzymy.
vizualizace vlnových funkcí a rozdělení náboje je náročná, protože vyžaduje zkoumání chování funkce tří proměnných v trojrozměrném prostoru. Tato vizualizace je usnadněna zvážením radiálních a úhlových částí samostatně, ale vykreslení radiálních a úhlových částí odděleně neodhalí tvar orbitalu velmi dobře. Tvar lze lépe odhalit v grafu hustoty pravděpodobnosti. Aby se takové trojrozměrné pozemku, rozdělit prostor do malé objemové prvky, vypočítat \(\psi^* \psi \) ve středu každého objem prvek, a pak odstín, tečkování nebo barvu, která objemu prvek v poměru k velikosti \(\psi^* \psi \). Nezaměňujte takové pozemky s polárními pozemky, které vypadají podobně.
hustoty pravděpodobnosti mohou být také reprezentovány obrysovými mapami, jak je znázorněno na obrázku \(\PageIndex{1}\).
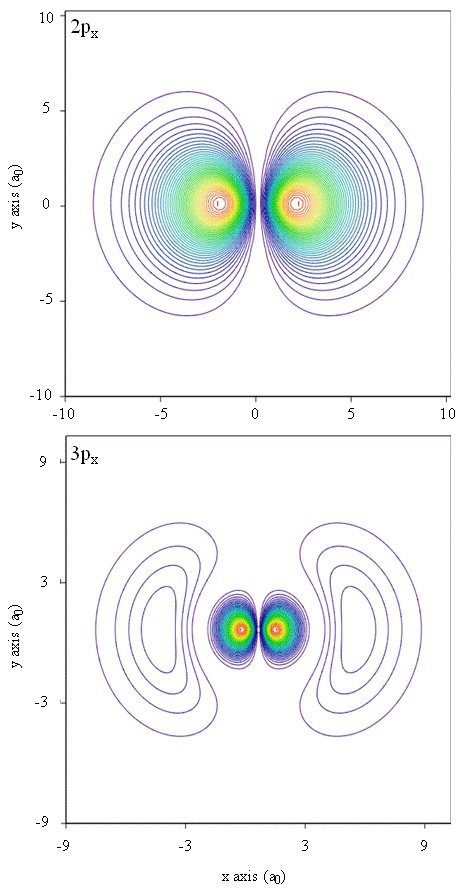
Další reprezentační technika, modelování virtuální reality, má velký příslib pro reprezentaci elektronových hustot. Představte si například schopnost zažít elektronovou hustotu jako sílu nebo odpor na hůlce, kterou se pohybujete trojrozměrným prostorem. Zařízení, jako jsou tato, nazývaná haptická zařízení, již existují a používají se k reprezentaci vědeckých informací. Stejně tak by nebylo zajímavé „létat“ atomovým orbitálem a zažít změny v elektronové hustotě jako změny barvy nebo změny oblačnosti? Speciálně navržené pokoje s 3D obrazovek a „chytré“ brýle, které poskytují zpětnou vazbu o směru pohled diváka jsou v současné době vyvíjeny, které nám umožní zažít takové pocity.
metody pro samostatné zkoumání radiálních částí atomových orbitalů poskytují užitečné informace o distribuci hustoty náboje uvnitř orbitalů. Grafy radiálních funkcí, \(R (r)\), pro orbitaly 1s, 2s a 2p vynesené na obrázku \(\PageIndex{2}\).
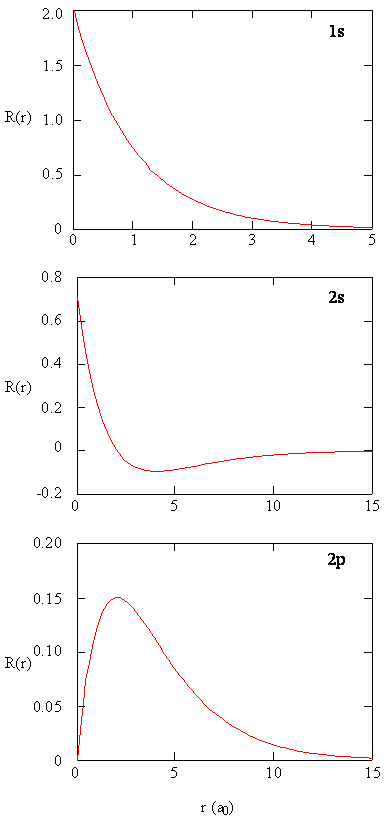
1s funkce na Obrázku \(\PageIndex{2}\) začíná s vysokou pozitivní hodnotu na jádro a exponenciálně rozpadá se v podstatě na nulu po 5 Bohrův poloměr. Vysoká hodnota v jádru může být překvapivá, ale jak uvidíme později, pravděpodobnost nalezení elektronu v jádru je mizivě malá.
další upozornění jak radiální funkce pro 2S orbital, obrázek \(\PageIndex{2}\), jde na nulu a stane se zápornou. Toto chování odhaluje přítomnost radiálního uzlu ve funkci. Radiální uzel nastane, když se radiální funkce rovná nule jiné než at \(r = 0\) nebo \(r = ∞\). Uzly a omezující chování atomových orbitálních funkcí jsou užitečné při identifikaci toho, který orbitál je popsán pomocí které vlnové funkce. Například všechny funkce s mají nenulové hodnoty vlnové funkce na \(r = 0\), ale p, d, f a všechny ostatní funkce jsou na počátku nulové. Je užitečné si uvědomit, že tam jsou \(n-1-l\) radiální uzly v wavefunction, což znamená, že 1s orbital nemá radiální uzly, 2s má jeden radiální uzel, a tak dále.
Cvičení \(\PageIndex{5}\)
Prozkoumat matematické formy radiální wavefunctions. Jaká funkce ve funkcích způsobuje, že některé z nich jdou na nulu na počátku, zatímco funkce s na počátku nejdou na nulu?
cvičení \(\PageIndex{6}\)
jaký matematický rys každé z radiálních funkcí řídí počet radiálních uzlů?
cvičení \(\PageIndex{7}\)
při jaké hodnotě r se vyskytuje radiální uzel 2s?
Cvičení \(\PageIndex{8}\)
vytvořte tabulku, která poskytuje energii, počet radiální uzly, a počet úhlové uzlů a celkový počet uzlů pro každou funkci s n = 1, 2, a 3. Určete vztah mezi energií a počtem uzlů. Určete vztah mezi počtem radiálních uzlů a počtem úhlových uzlů.
množství \(R (r) ^ * R (r)\) dává radiální hustotu pravděpodobnosti; tj. hustota pravděpodobnosti elektronu v bodě umístěném ve vzdálenosti \(r\) od protonu. Radiální hustoty pravděpodobnosti pro tři typy atomových orbitalů jsou vyneseny na obrázku (\PageIndex{3}\).
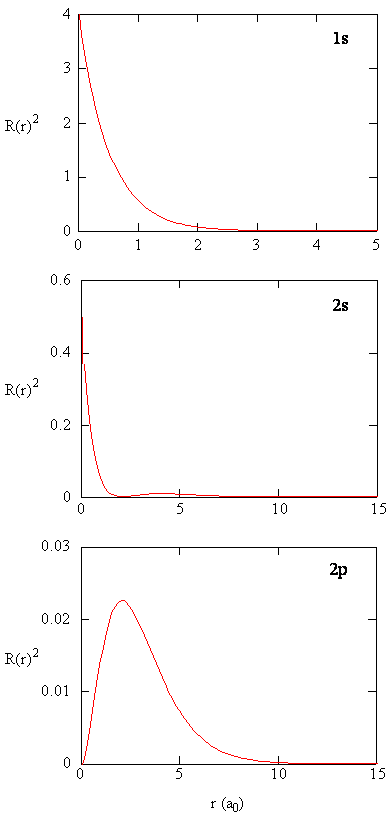
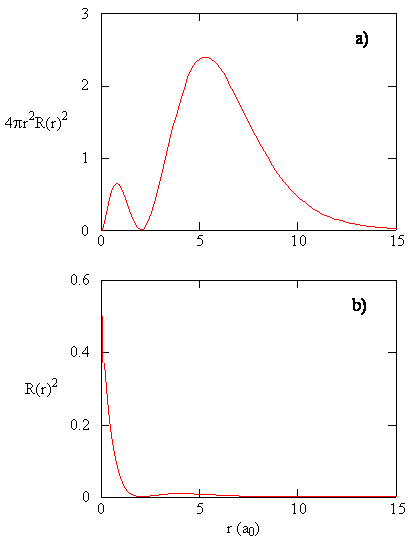
Když radiální hustoty pravděpodobnosti pro každou hodnotu r je násoben části kulové plochy zastoupeny konkrétní hodnotu r, dostaneme radiální distribuční funkce. Radiální distribuční funkce dává hustotu pravděpodobnosti pro elektron, který se nachází kdekoli na povrchu koule umístěné ve vzdálenosti r od protonu. Protože plocha sférického povrchu je \(4 \ pi r^2\), radiální distribuční funkce je dána \(4 \ pi r^2 R (r) ^* R (r)\).
radiální distribuční funkce jsou znázorněny na obrázku \(\PageIndex{4}\). Při malých hodnotách r je radiální distribuční funkce nízká, protože malá plocha pro malé poloměry moduluje vysokou hodnotu radiální hustoty pravděpodobnosti v blízkosti jádra. Jak zvyšujeme \(r\), plocha povrchu spojená s danou hodnotou r se zvětšuje a termín \(r^2\) způsobuje zvýšení radiální distribuční funkce, i když hustota radiální pravděpodobnosti začíná klesat. Při velkých hodnotách \(r\) exponenciální rozpad radiální funkce převažuje nad nárůstem způsobeným termínem \(r^2\) a radiální distribuční funkce klesá.
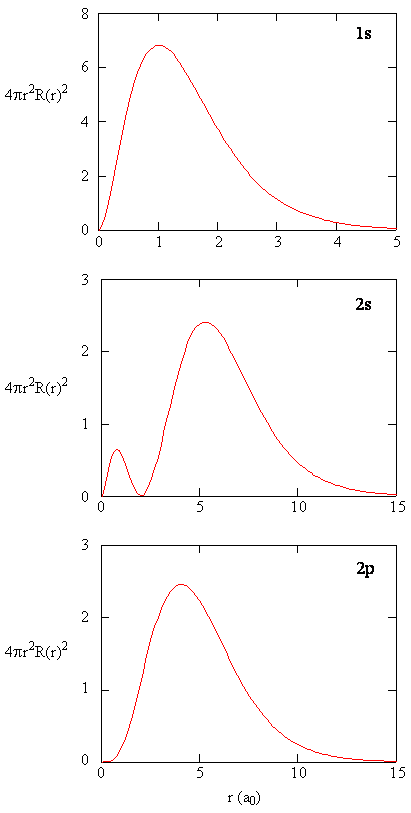
Cvičení \(\PageIndex{9}\)
Napsat kvalitní srovnání radiální funkce a radiální distribuční funkce pro 2s orbitalu. Viz Obrázek (\PageIndex{5}\)
Přispěvatelé a Pravomocí
-
David M. Hanson, Erica Harvey, Robert Sweeney, Tereza Julia Zielinski („Kvantové Stavy Atomů a Molekul“)