Třídící algoritmy jsou trapné kombinace zásadně nutné, a hluboce diskutabilní. Z nových inženýři snaží zapůsobit v rozhovoru pro starší inženýři hledají řešení, jak rychle škálování databáze, existuje bezpočet faktorů brát v úvahu. Jaká je rychlost srovnání mezi dvěma objekty? Jaká je doba výměny? Jak velká je databáze? Jaký typ objektů obsahuje? Je to již polořadovka? Musí být výsledky stabilní?

každá z těchto otázek může vyvozovat argumenty ve prospěch jednoho nebo druhého algoritmu. Jsou zdrojová data velká a složitá? Většina jazyků výchozí ke standardu, rychlé řazení s jeho o (n log n) časové složitosti. Je menší? Vložení třídění dělá divy na ty. Většinou tříděný? Sakra, třídění bublin by na to mohlo téměř fungovat. Chcete-li číst/vizualizovat zásluhy každého z nich, podívejte se na toto srovnání toptal.com.

jeden algoritmus třídění, který na tomto webu nenajdete, nebo téměř žádný jiný, je Tim Sort. Tento obskurní druh je v současné době jedinečný pro Python a používá se jako výchozí algoritmus třídění. Volání array.sort v Pythonu a Tim Sort je to, co se provádí. Přesto je vzácné najít inženýry, kteří znají a rozumějí Tim Sort. Takže: co to je?

Tim Druh byl poprvé realizován v roce 2002 Tim Peters pro použití v jazyce Python. Údajně pochází z pochopení, že většina třídící algoritmy jsou narozené ve školních třídách, a není určen pro praktické použití na reálných datech. Tim Sort využívá společných vzorů v datech a využívá kombinaci třídění sloučení a třídění vložení spolu s nějakou interní logikou pro optimalizaci manipulace s rozsáhlými daty.

Proč se Tim Nějak?

při pohledu na obrázek 2 můžeme okamžitě vidět něco zajímavého. V celé své kráse, Tim Sort překonává sloučit třídění a rychlé řazení. V nejhorším případě běží srovnatelnou rychlostí sloučení třídění a ve skutečnosti překonává rychlé řazení. Jinými slovy, je to nečekaně rychlé.

pokud jde o prostor, Tim Sort je na horším konci spektra, ale prostor pro většinu algoritmů třídění je docela řídký. O (n) není ve většině případů příliš hrubý; stojí za zmínku jako možný nedostatek a jedno místo, kde Quick Sort skutečně zastíní Tim Sort.

poslední položkou, na které jsou algoritmy třídění často posuzovány, je stabilita. Stabilita je koncept, že při třídění si objekty stejné hodnoty zachovávají své původní pořadí. Možná se divíte, proč nám na tom záleží. Položky mají stejnou hodnotu-proč nám vadí, jak jsou objednány?

jednoduchá odpověď je, že stabilita je důležitá pro skládané druhy. To znamená, že nejprve třídíte na základě jednoho kritéria, pak na základě druhého. Pokud to uděláte v nestabilním algoritmu, okamžitě ztratíte jakoukoli spolehlivost z prvního druhu při spuštění druhého. Pro referenci je rychlé řazení nestabilní a sloučení řazení je stabilní.

Tim Sort je také stabilní, nemluvě o rychlé, i když mírně těžké váze (ve srovnání pouze s Quick Sort). Zatímco algoritmy třídění mohou (a měly by) být posuzovány z jiných důvodů, jedná se o velké tři.

implementace ve třech krocích

Tim Sort je složitá, a to i podle algoritmických standardů. Implementace je nejlépe rozdělena na části.

binární vyhledávání

první věc, kterou potřebujete k implementaci třídění Tim, je metoda binárního vyhledávání. To se používá pouze k implementaci třídění vložení později.

Pro porovnání: Binární Vyhledávací Algoritmy,

Insertion Sort & Merge Sort

za Druhé, musíte kód Insertion Sort a Merge Sort. Jedná se o známé algoritmy a měly by být v zadní kapse většiny inženýrů, ale projdeme základy toho, jak fungují a proč jsou pro nás cenné.

Insertion Sort je velmi jednoduchý třídící algoritmus. Prochází polem a kdykoli narazí na položku, která je mimo provoz (striktně méně/více než položka před ní), přesune ji do příslušné pozice v již tříděném poli. Insertion Sort je proslulý tím, že pracuje velmi rychle na již tříděných polích, stejně jako na menších polích. Ve skutečnosti můžeme z obr. 2 vidět, že třídění vložení má působivý nejlepší čas běhu O (n). Mějte na paměti posun vpřed s tim Sort: nejlepším případem pro vložení třídění je již seřazené pole. Může to znít hloupě, ale to bude relevantní.

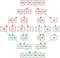
Merge Sort na druhou stranu funguje základní princip: je nesmírně snadné sloučit již seřazené pole. Takže rozděluje počáteční pole na polovinu znovu a znovu, dokud to není nic jiného než jednotlivé prvky. Pak se pomalu přestaví hlavní pole sloučením těchto prvků zpět dohromady v řazeném pořadí. Protože jsme začali ze stavebních bloků velikosti jedna, bylo velmi snadné vytvořit počáteční tříděná pole. Pak je snadné je sloučit. Nakonec trávíme O (n log n) čas, a (důležité) děláme to způsobem, který je zaručeně stabilní.

například implementace viz:

Merge Sort: https://www.geeksforgeeks.org/merge-sort/

Vložení Druh: https://www.geeksforgeeks.org/insertion-sort/

Implementovat Tim Trochu

klíčem k pochopení Tim Nějak provádění je pochopení jeho používání vede. Tim Sort využívá přirozeně se vyskytující přednastavená data ve svůj prospěch. Presorted máme jednoduše na mysli, že sekvenční prvky jsou všechny rostoucí nebo klesající (je nám jedno, které).

nejprve nastavíme minrun velikost. Tím máme na mysli to, že chceme zajistit, aby všechny naše běhy byly alespoň určité délky. Vezměte prosím na vědomí, že nezaručujeme, že najdeme běhy této velikosti-do toho se dostaneme později. Jednoduše říkáme, že běh musí mít alespoň určitou délku.

když narazíme na běh, odložíme jej stranou. Když najdeme nejdelší běh v rozsahu minrun. Nyní máme známou datovou strukturu: malé tříděné pole. Pokud je alespoň minrun v délce, pak huzzah! Můžeme jít dál. Pokud tomu tak není, vložíme do hry Typ vložení.

z výše uvedeného si možná pamatujete, že třídění Vkládání je zvláště účinné na dvou typech polí: malých a již tříděných. To, co jsme právě udělali, je malé, tříděné pole. Pokud to není alespoň minrun na délku, jsme dosáhnout toho a chytit dostatek jiných prvků, aby dokončit běh, pak použijte Vložení Druhu, aby se zasadila je do našich seřazené pole, rychlé a snadné. Je zřejmé, že pokud běh narazí na konec pole, můžete ho nechat trochu krátký.

jakmile vytvoříte všechny své běhy (tj. V nejlepším případě je celé pole již tříděno a Tim Sort je dostatečně chytrý, aby věděl, že nemusí dělat nic jiného. Jindy, má tendenci být jen velmi efektivní. Další výhodou je, že třídění vložení i třídění sloučení jsou stabilní, takže výsledné pole je stabilní.

pro ty, kteří dávají přednost kulkám:

1. Vytvořit minrun velikost, která je mocninou 2 (obvykle 32, nikdy více než 64 nebo vaše Insertion Sort ztratí účinnost)
2. Najít a spustit v první minrun dat.
3. v Případě, že běh není alespoň minrun na délku, použijte Vložení Druhu chytit následné nebo předchozí položky a vložte je do běhu, dokud to je, jaká minimální velikost.
4. opakujte, dokud nebude celé pole rozděleno do tříděných podsekcí.
5. pro spojení uspořádaných polí použijte druhou polovinu řazení sloučení.

závěr

Tim Sort je silný. Je rychlý a stabilní, ale možná nejdůležitější je, že využívá reálných vzorů a využívá je k vytvoření konečného produktu. Je to pro každou situaci? Asi ne. Hodně štěstí při programování na tabuli během rozhovoru, a pokud potřebujete jen rychlý jednoduchý algoritmus třídění v nouzi, pravděpodobně se nechcete obtěžovat implementací něčeho tak složitého. Pro datové vědce, kteří křupají čísla, však stojí za to se podívat.

pro zvědavé si můžete prohlédnout celý kód řazení Tim na Githubu.

díky

děkuji všem svým čtenářům. Vážím si vašeho času, a upřímně doufám, že jste našli obsah informativní. Máte-li jakékoli dotazy nebo odpovědi, neváhejte jeden klesnout níže.