V některých okolností, proud ve vinutí toroidní cívky přispívá pouze na B. pole uvnitř cívky a dělá žádný příspěvek magnetického pole B vně vinutí. Je to důsledek symetrie a Ampèrova obvodového zákona.

Dostatečné podmínky pro celkový vnitřní porodu B fieldEdit

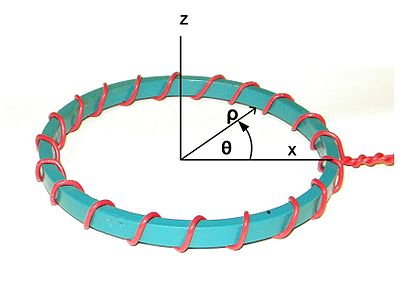Obr. 1. Graf. Osa Z je jmenovitá osa symetrie. Osa X zvolená libovolně, aby se vyrovnala s počátečním bodem vinutí. ρ se nazývá radiální směr. θ se nazývá obvodový směr.

Obr. 2. Axiálně symetrický toroidní induktor bez obvodového proudu.

absence obvodové proud (cesta obvodové aktuální stav je indikován červenou šipkou na obrázku 3 tohoto oddílu) a osově symetrické uspořádání vodičů a magnetické materiály jsou dostatečné podmínky pro celkový vnitřní porodu B pole. (Někteří autoři dávají přednost použití pole H). Kvůli symetrii musí linie toku B tvořit kruhy konstantní intenzity soustředěné na ose symetrie. Jediné linie toku B, které obklopují jakýkoli proud, jsou ty, které jsou uvnitř toroidálního vinutí. Proto z Ampérova obvodového zákona musí být intenzita pole B nulová mimo vinutí.

Obr. 3. Toroidní induktor s obvodovým proudem

obrázek 3 této části ukazuje nejběžnější toroidní vinutí. Nesplňuje oba požadavky na celkové omezení pole B. Při pohledu z osy je někdy vinutí na vnitřní straně jádra a někdy je na vnější straně jádra. V blízké oblasti není axiálně symetrický. Nicméně, v bodech vzdálenost několikanásobek rozteče vinutí, toroid vypadá symetricky. Stále existuje problém obvodového proudu. Bez ohledu na to, kolikrát vinutí obklopuje jádro, a bez ohledu na to, jak tenký drát, tento toroidní tlumivka bude stále patří jedné cívky smyčky v rovině anuloidu. Toto vinutí bude také produkovat a být citlivé na pole E v rovině induktoru.

obrázky 4-6 ukazují různé způsoby neutralizace obvodového proudu. Obrázek 4 je nejjednodušší a má tu výhodu, že zpětný vodič může být přidán po zakoupení nebo sestavení induktoru.

Obr. 4. Obvodový proud čelil zpětnému vodiči. Drát je bílý a vede mezi vnějším okrajem induktoru a vnější částí vinutí.

Obr. 5. Obvodový proud čelil zpětnému vinutí.

Obr. 6. Obvodový proud čelil dělenému zpětnému vinutí.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

Tam bude rozložení potenciálu podél vinutí. To může vést k E-poli v rovině toroidu a také k náchylnosti k e poli v rovině toroidu, jak je znázorněno na obrázku 7. To může být zmírněno použitím zpětného vinutí, jak je znázorněno na obrázku 8. S tímto vinutím se každé místo vinutí protíná, obě části budou mít stejnou a opačnou polaritu, což podstatně snižuje pole E generované v rovině.

Toroidní cívka/transformátor a magnetický vektor potentialEdit

Ukazuje vývoj magnetický vektorový potenciál kolem symetrická toroidní cívky.

viz Feynmanovy kapitoly 14 a 15 pro obecnou diskusi o magnetickém vektorovém potenciálu. Viz Feynman strana 15-11 pro diagram magnetického vektorového potenciálu kolem dlouhého tenkého solenoidu, který také vykazuje úplné vnitřní omezení pole B, alespoň v nekonečném limitu.

pole je přesné při použití předpoklad b f A = 0 {\displaystyle bf{A}=0}

. To by platilo za následujících předpokladů:

• 1. Coulombův měřič se používá
• 2. Lorenz měřidlo se používá a není tam žádný rozložení náboje ρ = 0 {\displaystyle \rho =0\,}
  
• 3. Používá se Lorenzův měřič a předpokládá se nulová frekvence
• 4. Lorenz měřidlo se používá a nenulovou frekvenci, která je dostatečně nízká, aby zanedbávat 1 c 2 ∂ ϕ ∂ t {\displaystyle {\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}}
  

  předpokládá.

číslo 4 se předpokládá pro zbytek tohoto oddílu a může být označováno jako „kvazi-statická podmínka“.

ačkoli axiálně symetrický toroidní induktor bez obvodového proudu zcela omezuje B pole uvnitř vinutí, pole A (potenciál magnetického vektoru) není omezeno. Šipka č. 1 na obrázku zobrazuje vektorový potenciál na ose symetrie. Radiální proudové úseky a A b jsou stejné vzdálenosti od osy, ale směřují opačným směrem,takže se zruší. Stejně tak se segmenty c A d ruší. Ve skutečnosti se všechny segmenty radiálního proudu zruší. Situace pro axiální proudy je odlišná. Axiální proud na vnější straně toroidu směřuje dolů a axiální proud na vnitřní straně toroidu směřuje nahoru. Každý segment axiálního proudu na vnější straně toroidu může být spojen se stejným, ale opačně zaměřeným segmentem na vnitřní straně toroidu. Segmenty na vnitřní straně jsou blíže než segmenty na vnější straně k ose, proto existuje čistá vzestupná složka pole A podél osy symetrie.

Představující magnetického vektorového potenciálu (A), magnetická indukce (B) a proudovou hustotou (j) pole kolem toroidní tlumivka s kruhovým průřezem. Tlustší čáry označují polní čáry s vyšší průměrnou intenzitou. Kruhy v průřezu jádra představují tok B vycházející z obrazu. Plus znaky na druhém průřezu jádra představují tok B, který jde do obrazu. Div a = 0 bylo předpokládáno.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ t → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

) mají stejný tvar, pak čáry a obrysy se vztahují k B jako čáry a obrysy B se vztahují k j. To znamená, zobrazení pole kolem smyčky B tok (jako by bylo vyrobené v toroidní tlumivku), je kvalitativně stejný jako B pole kolem smyčky proudu. Obrázek vlevo je umělcovo zobrazení pole a kolem toroidálního induktoru. Tlustší čáry označují cesty s vyšší průměrnou intenzitou (kratší cesty mají vyšší intenzitu, takže integrál dráhy je stejný). Čáry jsou jen nakresleny, aby vypadaly dobře a poskytovaly obecný vzhled pole A.

Toroidní transformátor akce v přítomnosti celkem B pole confinementEdit

E a B pole lze vypočítat z a ϕ {\displaystyle \phi \,}

(skalární elektrický potenciál) pole B = ∇ × A . {\displaystyle \ mathbf {B} =\nabla \ times \ mathbf {A} .}

a : E = − ∇ ϕ − ∂ A ∂ t {\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}

a tak, i když regionu mimo vinutí je prostý pole B, to je naplněné s nenulovou E pole. Množství ∂ V ∂ t {\displaystyle {\frac {\partial \mathbf {A} }{\partial t}}}

je zodpovědný za žádoucí magnetické pole spojení mezi primární a sekundární, zatímco množství ∇ ϕ {\displaystyle \nabla \phi \,}

je zodpovědný za nežádoucí elektrické pole spojení mezi primární a sekundární. Návrháři transformátorů se snaží minimalizovat spojku elektrického pole. Pro zbytek této sekce bude ∇ ϕ {\displaystyle \nabla \Phi\,}

nulová, pokud není uvedeno jinak.

Stokesova věta se vztahuje, tak, že dráhový integrál se rovná přiloženém B tok, stejně jako dráhový integrál B, je rovna konstantě krát přiložené aktuální

cesta integrál E podél sekundární vinutí dává sekundární je indukovaného EMF (Electro-Motive Force).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

, která říká, EMF je rovna čas, rychlost změny B tok ohraničená vinutí, což je obvyklý výsledek.

Toroidní transformátor Poyntingova vektoru tažné z primární na sekundární úroveň v přítomnosti celkem B pole confinementEdit

Na tomto obrázku, modré tečky ukazují, kde B tok z primární proud přichází z obrázku a znaménka plus značí, kde to jde do obrázku.

vysvětlení číslaedit

tento obrázek ukazuje poloviční část toroidního transformátoru. Předpokládají se kvazistatické podmínky, takže fáze každého pole je všude stejná. Transformátor, jeho vinutí a všechny věci jsou rozloženy symetricky kolem osy symetrie. Vinutí jsou taková, že neexistuje obvodový proud. Požadavky jsou splněny pro úplné vnitřní omezení pole B v důsledku primárního proudu. Jádro a primární vinutí jsou reprezentovány šedohnědým torusem. Primární vinutí není zobrazeno, ale proud ve vinutí na ploše průřezu je zobrazen jako zlaté (nebo oranžové) elipsy. B pole způsobené primárním proudem je zcela omezeno na oblast uzavřenou primárním vinutím (tj. Modré tečky na průřezu levé ruky ukazují, že čáry toku B v jádru vycházejí z průřezu levé ruky. Na druhém průřezu modré značky plus označují, že tam vstupuje tok B. Pole E pocházející z primárních proudů je zobrazeno jako zelené elipsy. Sekundární vinutí je znázorněno jako hnědá čára přicházející přímo dolů po ose symetrie. V běžné praxi, na obou koncích sekundární jsou spojeny s dlouhý drát, který zůstává daleko od toru, ale k udržení absolutní osová symetrie, celý přístroj je koncipován jako být uvnitř dokonale vodivé koule s sekundární drát „zaracha“, aby se uvnitř koule na každém konci. Sekundární je vyroben z odporového drátu, takže nedochází k samostatnému zatížení. Pole E podél sekundárního způsobuje proud v sekundárním (žluté šipky), který způsobuje pole B kolem sekundárního (zobrazeno jako modré elipsy). Toto pole B vyplňuje prostor, včetně uvnitř jádra transformátoru, takže na konci je nepřetržité nenulové pole B od primárního k sekundárnímu, pokud sekundární není otevřený obvod. Vektorový součin E pole (pocházel z primární proudy) a B pole (získávány ze sekundárních proudů) tvoří Poyntingova vektoru, které body od primární k sekundární.