8.2: bølgefunktionerne
opløsningerne til hydrogenatomet Schr Schrdinger ligning er funktioner, der er produkter af en sfærisk harmonisk funktion og en radial funktion.
\
bølgefunktionerne for hydrogenatomet afhænger af de tre variabler r, \(\theta\) og \(\varphi \) og de tre kvantetal n, \(l\) og \(m_l\). Variablerne giver elektronens position i forhold til protonen i sfæriske koordinater. Den absolutte firkant af bølgefunktionen, \ (|\psi (r, \ theta, \ varphi) / ^2\), evalueret ved \(r\), \(\theta\) og \(\varphi\) giver sandsynlighedstætheden for at finde elektronen inde i et differentielt volumen \(d \tau\), centreret ved den position, der er angivet af r, \(\theta\) og \(\varphi\).
øvelse \(\Sideindeks{1}\)
Hvad er værdien af integralet
\
kvantetallene har Navne: \(n\) kaldes det primære kvantetal, \(l\) kaldes vinkelmoment kvantetal, og \(m_l\) kaldes det magnetiske kvantetal, fordi(som vi vil se i afsnit 8.4) energien i et magnetfelt afhænger af \(m_l\). Ofte kaldes \(l\) det asimutale kvantetal, fordi det er en konsekvens af \(\theta\)-ligningen, som involverer den asimutale vinkel \(\Theta\), der henviser til vinklen til top.
disse kvantetal har specifikke værdier, der dikteres af de fysiske begrænsninger eller grænsevilkår, der pålægges Schr-Kristdinger-ligningen: \(n\) skal være et heltal større end 0, \(l\) kan have værdierne 0 til n‑1, og \(m_l\) kan have \(2L + 1\) Værdier, der spænder fra \(-l\) ‑ til \(+l\) i enhed eller heltal trin. Værdierne for kvantetallet \(l\) kodes normalt med et bogstav: s betyder 0, p betyder 1, d betyder 2, f betyder 3; de næste koder fortsætter alfabetisk (f.eks. g betyder \(l = 4\)). Kvantetallene angiver kvantiseringen af fysiske mængder. De diskrete energier i forskellige tilstande af hydrogenatomet er givet af \(n\), størrelsen af vinkelmomentet er givet af \(l\), og en komponent af vinkelmomentet (normalt valgt af kemikere til at være s‑komponenten) er givet af \(m_l\). Det samlede antal orbitaler med en bestemt værdi af \(n\) er \(n^2\).
øvelse \(\Sideindeks{2}\)
overvej flere værdier for n, og vis at antallet af orbitaler for hver n er \(n^2\).
øvelse \(\Sideindeks{3}\)
Konstruer en tabel, der opsummerer de tilladte værdier for kvantetallene n, \(l\) og \(m_l\). for energiniveauer 1 til 7 af brint.
øvelse \(\Sideindeks{4}\)
notationen 3D specificerer kvantetallene for en elektron i hydrogenatomet. Hvad er værdierne for n og \(l\) ? Hvad er værdierne for energi og vinkelmoment? Hvad er de mulige værdier for det magnetiske kvantetal? Hvad er de mulige retninger for vinkelmomentvektoren?
hydrogenatomets bølgefunktioner, \(\psi (r, \theta , \varphi )\), kaldes atomorbitaler. En atom orbital er en funktion, der beskriver en elektron i et atom. Bølgefunktionen med n = 1, \(l=1\) og \(m_l\) = 0 kaldes 1s orbital, og en elektron, der er beskrevet af denne funktion, siges at være “i” ls orbital, dvs.har en 1s orbital tilstand. Begrænsningerne på \(n\), \(l)\) og \(m_l\), der pålægges under opløsningen af brintatomet Schr Kritdinger ligning forklarer, hvorfor der er en enkelt 1s orbital, hvorfor der er tre 2P orbitaler, fem 3D orbitaler osv. Vi vil se, når vi overvejer multielektronatomer i kapitel 9, at disse begrænsninger forklarer funktionerne i det periodiske system. Med andre ord, det periodiske system er en manifestation af Schr-Kristdinger-modellen og de fysiske begrænsninger, der pålægges for at opnå opløsningerne til Schr-Kristdinger-ligningen for hydrogenatomet.
visualisering af variationen af en elektronisk bølgefunktion med \(r\), \(\theta\) og \(\varphi\) er vigtig, fordi den absolutte firkant af bølgefunktionen viser ladningsfordelingen (elektronsandsynlighedstæthed) i et atom eller molekyle. Ladningsfordelingen er central for kemi, fordi den er relateret til kemisk reaktivitet. For eksempel tiltrækkes en elektronmangel del af et molekyle til en elektronrig region af et andet molekyle, og sådanne interaktioner spiller en vigtig rolle i kemiske interaktioner, der spænder fra substitutions-og additionsreaktioner til proteinfoldning og interaktionen mellem substrater med f.eks.visualisering af bølgefunktioner og ladningsfordelinger er udfordrende, fordi det kræver at undersøge opførslen af en funktion af tre variabler i tredimensionelt rum. Denne visualisering gøres lettere ved at overveje de radiale og kantede dele separat, men at plotte de radiale og kantede dele separat afslører ikke formen på en orbital særlig godt. Formen kan afsløres bedre i et sandsynlighedstæthedsplot. For at lave et sådant tredimensionelt plot skal du opdele rummet i små volumenelementer, beregne \(\psi^* \psi \) i midten af hvert volumenelement og derefter skygge, stipple eller farve det volumenelement i forhold til størrelsen af \(\psi^* \psi \). Forveks ikke sådanne tomter med polære tomter, der ligner hinanden.
Sandsynlighedstætheder kan også repræsenteres af konturkort, som vist i figur \(\Sideindeks{1}\).
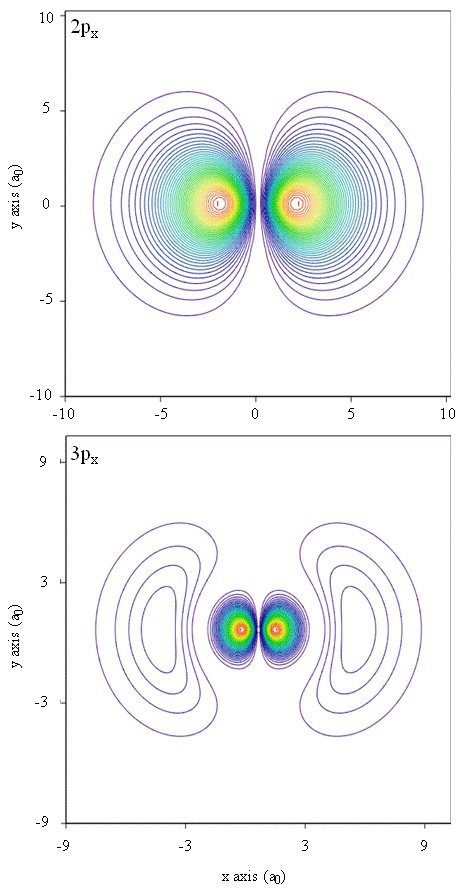
en anden repræsentationsteknik, virtual reality modeling, har et stort løfte om repræsentation af elektrontætheder. Forestil dig for eksempel at være i stand til at opleve elektrontæthed som en kraft eller modstand på en stav, som du bevæger dig gennem tredimensionelt rum. Enheder som disse, kaldet haptiske enheder, findes allerede og bruges til at repræsentere videnskabelig information. Tilsvarende ville det ikke være interessant at “flyve” gennem en atombane og opleve ændringer i elektrondensitet, når farveændringer eller uklarhed ændres? Specialdesignede værelser med 3D-skærme og “smarte” briller, der giver feedback om retningen af seerens blik, udvikles i øjeblikket for at give os mulighed for at opleve sådanne fornemmelser.
metoder til separat undersøgelse af de radiale dele af atomorbitaler giver nyttige oplysninger om fordelingen af ladningstæthed inden for orbitalerne. Grafer over de radiale funktioner, \(R(r)\), for 1s, 2s og 2p orbitaler afbildet i figur \(\Sideindeks{2}\).
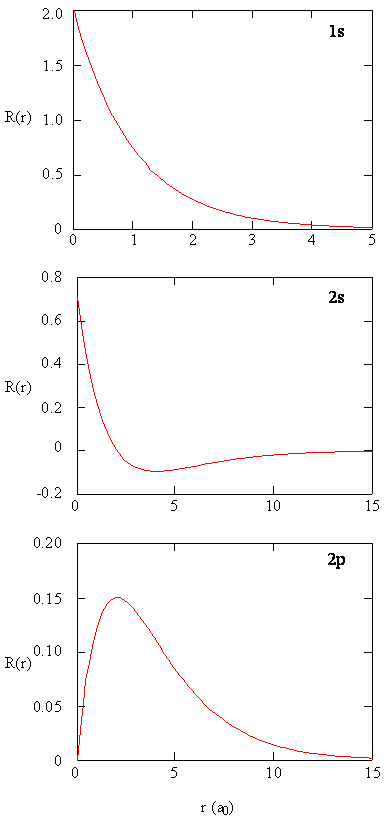
1s-funktionen i figur \(\Sideindeks{2}\) starter med en høj positiv værdi ved kernen og eksponentielt henfalder til i det væsentlige nul efter 5 Bohr-radier. Den høje værdi ved kernen kan være overraskende, men som vi skal se senere, er sandsynligheden for at finde en elektron ved kernen forsvindende lille.
næste bemærk, hvordan den radiale funktion for 2s orbital, figur \(\Sideindeks{2}\), går til nul og bliver negativ. Denne adfærd afslører tilstedeværelsen af en radial knude i funktionen. En radial node opstår, når den radiale funktion er lig med nul andet end ved \(r = 0\) eller \(r = liter\). Noder og begrænsende adfærd af atomære orbitalfunktioner er begge nyttige til at identificere, hvilken orbital der beskrives ved hvilken bølgefunktion. For eksempel har alle s-funktionerne ikke-nul bølgefunktionsværdier ved \(r = 0\), men p, d, f og alle andre funktioner går til nul ved oprindelsen. Det er nyttigt at huske, at der er \(n-1-l\) radiale noder i en bølgefunktion, hvilket betyder, at en 1s orbital ikke har radiale noder, en 2s har en radial knude osv.
øvelse \(\Sideindeks{5}\)
Undersøg de matematiske former for de radiale bølgefunktioner. Hvilken funktion i funktionerne får nogle af dem til at gå til nul ved oprindelsen, mens S-funktionerne ikke går til nul ved oprindelsen?
øvelse \(\Sideindeks{6}\)
hvilket matematisk træk ved hver af de radiale funktioner styrer antallet af radiale noder?
øvelse \(\Sideindeks{7}\)
Ved hvilken værdi af r forekommer 2s radial node?
øvelse \(\Sideindeks{8}\)
lav en tabel, der giver energien, antallet af radiale noder og antallet af vinkelnoder og det samlede antal noder for hver funktion med n = 1, 2 og 3. Identificer forholdet mellem energien og antallet af noder. Identificer forholdet mellem antallet af radiale noder og antallet af vinkelknuder.
mængden \(R (r) ^* R(r)\) giver den radiale sandsynlighedstæthed; dvs.sandsynlighedstætheden for elektronen at være på et punkt placeret afstanden \(r\) fra protonen. Radiale sandsynlighedstætheder for tre typer atomorbitaler er afbildet i figur (\Sideindeks{3}\).
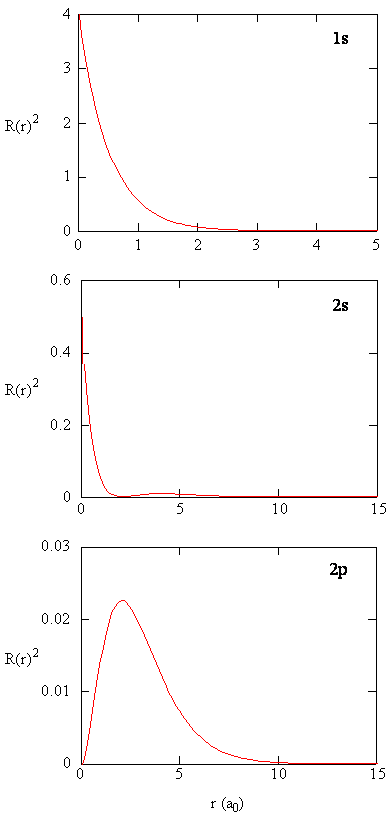
når den radiale sandsynlighedstæthed for hver værdi af r multipliceres med arealet af den sfæriske overflade repræsenteret af den særlige værdi af r, får vi den radiale fordelingsfunktion. Den radiale fordelingsfunktion giver sandsynlighedstætheden for, at en elektron findes overalt på overfladen af en kugle placeret en afstand r fra protonen. Da arealet af en sfærisk overflade er \(4\ pi r^2\), er den radiale fordelingsfunktion givet af \(4\pi r^2 R(r) ^* R(r)\).
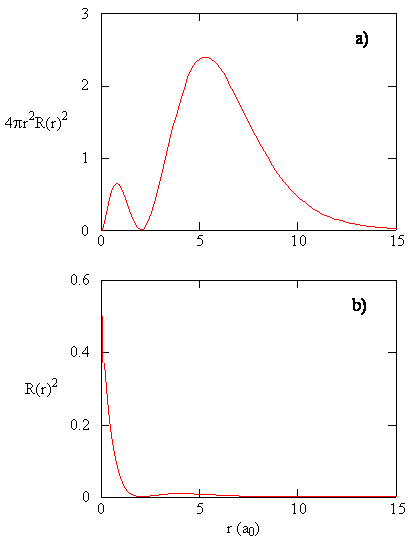
Radialfordelingsfunktioner er vist i figur \(\Sideindeks{4}\). Ved små værdier af r er den radiale fordelingsfunktion lav, fordi det lille overfladeareal for små radier modulerer den høje værdi af den radiale sandsynlighedstæthedsfunktion nær kernen. Når vi øger \(r\), øges overfladearealet forbundet med en given værdi af r, og udtrykket \(r^2\) får den radiale fordelingsfunktion til at stige, selvom den radiale sandsynlighedstæthed begynder at falde. Ved store værdier af \(r\) opvejer det eksponentielle henfald af den radiale funktion stigningen forårsaget af udtrykket \(r^2\), og den radiale fordelingsfunktion falder.
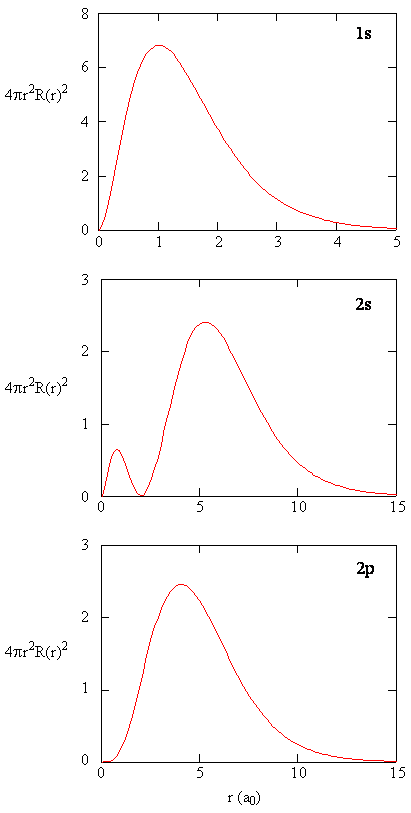
øvelse \(\Sideindeks{9}\)
Skriv en kvalitetssammenligning af radialfunktionen og radialfordelingsfunktionen for 2s orbital. Se figur (\Sideindeks{5}\)
bidragsydere og tilskrivninger
-
David M. Hanson, Erica Harvey, Robert Sveney, Theresa Julia Sielinski (“kvantetilstande af atomer og molekyler”)