alle regressionsteknikker indeholder en enkelt output (respons) variabel og en eller flere input (predictor) variabler. Outputvariablen er numerisk. Den generelle regressionstræbygningsmetode gør det muligt for inputvariabler at være en blanding af kontinuerlige og kategoriske variabler. Et beslutningstræ genereres, når hver beslutningsknude i træet indeholder en test på en eller anden inputvariabels værdi. Træets terminalnoder indeholder de forudsagte outputvariabelværdier.

et Regressionstræ kan betragtes som en variant af beslutningstræer, der er designet til at tilnærme reelle værdifunktioner i stedet for at blive brugt til klassificeringsmetoder.

metodologi

et regressionstræ er bygget gennem en proces kendt som binær rekursiv partitionering, som er en iterativ proces, der opdeler dataene i partitioner eller grene og derefter fortsætter med at opdele hver partition i mindre grupper, når metoden bevæger sig op ad hver gren.

oprindeligt grupperes alle poster i træningssættet (præklassificerede poster, der bruges til at bestemme træets struktur) i den samme partition. Algoritmen begynder derefter at allokere dataene i de to første partitioner eller grene ved hjælp af enhver mulig binær opdeling på hvert felt. Algoritmen vælger opdelingen, der minimerer summen af de kvadratiske afvigelser fra gennemsnittet i de to separate partitioner. Denne opdelingsregel anvendes derefter på hver af de nye grene. Denne proces fortsætter, indtil hver node når en brugerdefineret minimum node størrelse og bliver en terminal node. (Hvis summen af kvadrerede afvigelser fra gennemsnittet i en node er nul, betragtes denne node som en terminal node, selvom den ikke har nået minimumsstørrelsen.)

beskæring af træet

da træet dyrkes fra træningssættet, lider et fuldt udviklet træ typisk af overmontering (dvs.det forklarer tilfældige elementer i træningssættet, der sandsynligvis ikke er træk ved den større befolkning). Denne overmontering resulterer i dårlig ydeevne på virkelige data. Derfor skal træet beskæres ved hjælp af Valideringssættet. Ved hvert trin under træets vækst beregner lminer omkostningskompleksitetsfaktoren og bestemmer antallet af beslutningsnoder i det beskårne træ. Omkostningskompleksitetsfaktoren er den multiplikative faktor, der anvendes på træets størrelse (målt ved antallet af terminalknudepunkter).

træet beskæres for at minimere summen af: 1) outputvariablen varians i valideringsdataene, taget en terminalknude ad gangen; og 2) produktet af omkostningskompleksitetsfaktoren og antallet af terminalnoder. Hvis omkostningskompleksitetsfaktoren er angivet som nul, er beskæring simpelthen at finde det træ, der fungerer bedst på valideringsdata med hensyn til total terminalnudevarians. Større værdier af omkostningskompleksitetsfaktoren resulterer i mindre træer. Beskæring udføres på en sidste – i-første-ud-basis, hvilket betyder, at den sidst dyrkede knude er den første, der er genstand for eliminering. v2015 tilbyder tre kraftfulde ensemblemetoder til brug med Regressionstræer: sække (bootstrap aggregering), boosting og tilfældige træer. Regressionstræalgoritmen kan bruges til at finde en model, der resulterer i gode forudsigelser for de nye data. Vi kan se statistikker og forvirringsmatricer for den nuværende forudsigelse for at se, om vores model passer godt til dataene; men hvordan ville vi vide, om der er en bedre forudsigelse, der bare venter på at blive fundet? Svaret er, at vi ikke ved, om der findes en bedre forudsigelse. Imidlertid giver ensemblemetoder os mulighed for at kombinere flere svage regressionstræmodeller, som når de tages sammen danner en ny, nøjagtig, stærk regressionstræmodel. Disse metoder fungerer ved at oprette flere forskellige regressionsmodeller ved at tage forskellige prøver af det originale datasæt og derefter kombinere deres output. (Output kan kombineres ved hjælp af flere teknikker for eksempel flertalsafstemning for klassificering og gennemsnit for regression) denne kombination af modeller reducerer effektivt variansen i den stærke model. De tre typer ensemblemetoder, der tilbydes i sække, boosting og tilfældige træer, adskiller sig på tre punkter: 1) Valg af træningssæt for hver forudsigelse eller svag model; 2) Hvordan de svage modeller genereres; og 3) Hvordan output kombineres. I alle tre metoder trænes hver svag model på hele træningssættet for at blive dygtig i en del af datasættet.

Bagging (bootstrap aggregating) var en af de første ensemblealgoritmer, der nogensinde blev skrevet. Det er en simpel algoritme, men alligevel meget effektiv. Sække genererer flere træningssæt ved hjælp af tilfældig prøveudtagning med udskiftning (bootstrap sampling), anvender regressionstræalgoritmen på hvert datasæt og tager derefter gennemsnittet blandt modellerne for at beregne forudsigelserne for de nye data. Den største fordel ved sække er den relative lethed, at algoritmen kan paralleliseres, hvilket gør det til et bedre valg for meget store datasæt.

Boosting bygger en stærk model ved successivt at træne modeller til at koncentrere sig om poster, der modtager unøjagtige forudsagte værdier i tidligere modeller. Når de er færdige, kombineres alle forudsigere med en vægtet flertalsafstemning. Vi tilbyder tre varianter af boosting som implementeret af AdaBoost-algoritmen (en af de mest populære ensemblealgoritmer, der er i brug i dag): M1 (Freund), M1 (Breiman) og SAMME (trinvis additiv modellering ved hjælp af en eksponentiel i flere klasser).

Adaboost.M1 tildeler først en vægt (VB (i)) til hver post eller observation. Denne vægt er oprindeligt indstillet til 1/n og vil blive opdateret på hver iteration af algoritmen. Et originalt regressionstræ oprettes ved hjælp af dette første træningssæt (Tb), og en fejl beregnes som

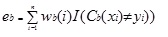
hvor funktionen i() returnerer 1, hvis sand og 0, hvis ikke.

fejlen i regressionstræet i bth-iterationen bruges til at beregne konstanten ?b. Denne konstant bruges til at opdatere vægten (VB(i). I AdaBoost.M1 (Freund), konstanten beregnes som

ab= ln ((1-eb)/eb)

i AdaBoost.M1 (Breiman) beregnes konstanten som

ab= 1/2LN ((1-eb)/eb)

i SAMME beregnes konstanten som

ab= 1/2LN ((1-eb)/eb + Ln (k-1) Hvor k er antallet af klasser

hvor antallet af kategorier er lig med 2, SAMME opfører sig som AdaBoost Breiman.

i en af de tre implementeringer (Freund, Breiman eller SAMME) vil den nye vægt for (b + 1)iterationen være

bagefter justeres vægtene alle til summen af 1. Som et resultat øges de vægte, der er tildelt de observationer, der blev tildelt unøjagtige forudsagte værdier, og de vægte, der er tildelt de observationer, der blev tildelt nøjagtige forudsagte værdier, reduceres. Denne justering tvinger den næste regressionsmodel til at lægge mere vægt på de poster, der blev tildelt unøjagtige forudsigelser. (Dette ? konstant bruges også i den endelige beregning, hvilket vil give regressionsmodellen med den laveste fejl mere indflydelse.) Denne proces gentages indtil b = antal svage elever. Algoritmen beregner derefter det vægtede gennemsnit blandt alle svage elever og tildeler denne værdi til posten. Boosting giver generelt bedre modeller end sække; det har dog en ulempe, da det ikke er paralleliserbart. Som et resultat, hvis antallet af svage elever er stort, ville boosting ikke være egnet.

metoden med tilfældige træer (tilfældige skove) er en variation af sække. Denne metode fungerer ved at træne flere svage regressionstræer ved hjælp af et fast antal tilfældigt udvalgte funktioner (KVRT til klassificering og antal funktioner/3 til forudsigelse), tager derefter gennemsnitsværdien for de svage elever og tildeler denne værdi til den stærke forudsigelse. Typisk kan antallet af genererede svage træer variere fra flere hundrede til flere tusinde afhængigt af træningssættets størrelse og sværhedsgrad. Tilfældige træer er paralleliserbare, da de er en variant af sække. Men da tandom træer vælger en begrænset mængde funktioner i hver iteration, udførelsen af tilfældige træer er hurtigere end sække.

Regressionstræ Ensemble metoder er meget kraftfulde metoder og resulterer typisk i bedre ydeevne end et enkelt træ. Denne funktion tilføjelse i v2015 giver mere præcise forudsigelse modeller, og bør overvejes i løbet af enkelt træ metode.