under nogle omstændigheder bidrager strømmen i viklingen af en toroidal induktor kun til B-feltet inde i viklingerne og bidrager ikke til det magnetiske B-felt uden for viklingerne. Dette er en konsekvens af symmetry og amp Kurtres kredsløbslov.

tilstrækkelige betingelser for total intern indespærring af B-feltetredit

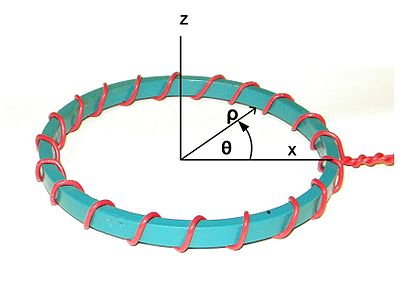fig. 1. Koordinatsystem. Aksen er den nominelle symmetriakse. Aksen valgt vilkårligt at line op med udgangspunktet for viklingen. det kaldes den radiale retning. det kaldes den perifere retning.

Fig. 2. En aksialt symmetrisk toroidal induktor uden omkredsstrøm.

fraværet af omkredsstrøm (stien til omkredsstrøm er angivet med den røde pil i figur 3 i dette afsnit) og det aksialt symmetriske layout af ledere og magnetiske materialer er tilstrækkelige betingelser for total intern indeslutning af B-feltet. (Nogle forfattere foretrækker at bruge H-feltet). På grund af symmetrien skal linjerne med B-strømning danne cirkler med konstant intensitet centreret på symmetriaksen. De eneste linjer med B-strømning, der omslutter enhver strøm, er dem, der er inde i den toroidale vikling. Derfor skal intensiteten af B-feltet fra Amperes kredsløbslov være nul uden for viklingerne.

Fig. 3. Toroidal induktor med omkredsstrøm

figur 3 i dette afsnit viser den mest almindelige toroidale vikling. Det mislykkes begge krav til total B feltindeslutning. Når man ser ud fra aksen, er viklingen undertiden på indersiden af kernen, og nogle gange er den på ydersiden af kernen. Det er ikke aksialt symmetrisk i den nærmeste region. Imidlertid, på punkter en afstand på flere gange viklingsafstanden, toroiden ser symmetrisk ud. Der er stadig problemet med den perifere strøm. Uanset hvor mange gange viklingen omslutter kernen, og uanset hvor tynd ledningen er, vil denne toroidale induktor stadig indeholde en enspolesløjfe i toroidplanet. Denne vikling vil også producere og være modtagelig for et e-felt i induktorens plan.

figur 4-6 viser forskellige måder at neutralisere omkredsstrømmen på. Figur 4 er den enkleste og har den fordel, at returledningen kan tilføjes, efter at induktoren er købt eller bygget.

Fig. 4. Omkredsstrøm modvirkes med en returledning. Ledningen er hvid og løber mellem induktorens ydre kant og den ydre del af viklingen.

Fig. 5. Omkredsstrøm modvirkes med en returvikling.

Fig. 6. Omkredsstrøm modvirkes med en split returvikling.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

der vil være en fordeling af potentialet langs viklingen. Dette kan føre til et E-felt i toroidplanet og også en modtagelighed for et E-felt i toroidplanet som vist i figur 7. Dette kan afhjælpes ved hjælp af en returvikling som vist på figur 8. Med denne vikling, hvert sted viklingen krydser sig selv, vil de to dele være på lige og modsat polaritet, hvilket væsentligt reducerer e-feltet genereret i Planet.

Toroidal induktor/transformer og magnetisk vektorpotentialedit

se Feynman Kapitel 14 og 15 for en generel diskussion af magnetisk vektorpotentiale. Se Feynman side 15-11 for et diagram over det magnetiske vektorpotentiale omkring en lang tynd magnetventil, som også udviser total intern indeslutning af B-feltet, i det mindste i den uendelige grænse.

a-feltet er nøjagtigt, når du bruger antagelsen b f A = 0 {\displaystyle bf{a}=0}

. Dette ville være sandt under følgende antagelser:

• 1. Coulomb-måleren bruges
• 2. der er ingen fordeling af ladningen, l = 0 {\displaystyle \ rho =0\,}
  
• 3. der anvendes en Nulfrekvens, og nulfrekvensen antages
• 4. en frekvens, der ikke er nul, der er lav nok til at forsømme 1 c 2, der er lav nok til at forsømme 1 c 2, der er 1 {\displaystyle {\frac {1}{c^{2}} {\frac {\partial \Phi} {\partial t}}}
  antages.

  nummer 4 antages for resten af dette afsnit og kan henvises til den “kvasi-statiske tilstand”.

  selvom den aksialt symmetriske toroidale induktor uden omkredsstrøm fuldstændigt begrænser B-feltet inden for viklingerne, er a-feltet (magnetisk vektorpotentiale) ikke begrænset. Pil #1 på billedet viser vektorpotentialet på symmetriaksen. Radiale strømafsnit a og b er lige store afstande fra aksen, men pegede i modsatte retninger, så de vil annullere. Ligeledes annullerer segmenter c og d. Faktisk annullerer alle de radiale strømsegmenter. Situationen for aksiale strømme er anderledes. Den aksiale strøm på ydersiden af toroiden peges ned, og den aksiale strøm på indersiden af toroiden peges op. Hvert aksialt strømsegment på ydersiden af toroiden kan matches med et lige, men modsat rettet segment på indersiden af toroiden. Segmenterne på indersiden er tættere end segmenterne på ydersiden til aksen, derfor er der en netto opadgående komponent af A-feltet langs symmetriaksen.

  

  repræsenterer det magnetiske vektorpotentiale (a), magnetisk strøm (B) og strømtæthed (j) felter omkring en toroidal induktor med cirkulært tværsnit. Tykkere linjer angiver feltlinjer med højere gennemsnitsintensitet. Cirkler i tværsnit af kernen repræsenterer B strøm, der kommer ud af billedet. Plustegn på det andet tværsnit af kernen repræsenterer B-strømmen, der går ind i billedet. Div a = 0 er blevet antaget.

  Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

  

  , and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

  

  (assuming quasi-static conditions, i.e. 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightar 0}

  

  ) har den samme form, så linierne og konturerne af A relaterer til B ligesom linjerne og konturerne af B relaterer til j. således er en skildring af A-feltet omkring en sløjfe af B, der er forbundet med strømning (som ville blive produceret i en toroidal induktor) er kvalitativt den samme som b-feltet omkring en strømsløjfe. Figuren til venstre er en kunstners skildring af A-feltet omkring en toroidal induktor. De tykkere linjer angiver stier med højere gennemsnitlig intensitet (kortere stier har højere intensitet, så stiintegralet er det samme). Linjerne er bare tegnet for at se godt ud og give det generelle udseende af A-feltet.

  Toroidal transformer handling i nærvær af total B feltindeslutningredit

  E-og B-felterne kan beregnes ud fra A-og lysfelterne {\displaystyle \phi\,}

  

  (skalar elektrisk potentiale) felter B = Kurt A . {\displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {A} .}

  

  og : E = − − – – — – – – – – – – – t {\displaystyle \mathbf {E} = – \nabla \Phi – {\frac {\partial \mathbf {a} }{\partial t}}}

  

  og så selvom regionen uden for viklingerne er blottet for b-felt, er den fyldt med ikke-nul e-felt. Mængden af lusset a lusset t {\displaystyle {\frac {\partial \mathbf {a} }{\partial t}}}

  

  er ansvarlig for den ønskelige magnetfeltkobling mellem primær og sekundær, mens mængden lusset {\displaystyle \nabla \Phi\,}

  

  er ansvarlig for den uønskede elektriske feltkobling mellem primær og sekundær. Transformer designere forsøger at minimere den elektriske feltkobling. For resten af dette afsnit antages det, at {\displaystyle \nabla \Phi \,}

  

  er nul, medmindre andet er angivet. Stokes sætning gælder, således at stiintegralet af A er lig med den lukkede B-strøm, ligesom stiintegralet B er lig med en konstant gange den lukkede strøm

  stiintegralet af E langs sekundærviklingen giver sekundærens inducerede EMF (Elektro-motivkraft).

  E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

  

  hvilket siger, at EMF er lig med den tidshastighed for ændring af B-strømmen, der er lukket af viklingen, hvilket er det sædvanlige resultat.

  Toroidal transformer Poynting vektorkobling fra primær til sekundær i nærvær af total B feltindeslutningredit

  

  i dette figur, blå prikker angiver, hvor B strøm fra den primære strøm kommer ud af billedet, og plustegn angiver, hvor det går ind i billedet.

  forklaring af figurenrediger

  denne figur viser den halve sektion af en toroidal transformer. Kvasi-statiske forhold antages, så fasen af hvert felt er overalt den samme. Transformeren, dens viklinger og alle ting fordeles symmetrisk omkring symmetriaksen. Viklingerne er sådan, at der ikke er nogen omkredsstrøm. Kravene er opfyldt for fuld intern indeslutning af B-feltet på grund af den primære strøm. Kernen og den primære vikling er repræsenteret af den gråbrune torus. Den primære vikling er ikke vist, men strømmen i viklingen ved tværsnitsoverfladen er vist som guld (eller orange) ellipser. B-feltet forårsaget af den primære strøm er helt begrænset til det område, der er omgivet af den primære vikling (dvs.kernen). Blå prikker i venstre tværsnit indikerer, at linjer med B-strømning i kernen kommer ud af venstre tværsnit. På det andet tværsnit indikerer blå plustegn, at B-strømmen kommer ind der. E-feltet, der stammer fra de primære strømme, vises som grønne ellipser. Sekundærviklingen er vist som en brun linje, der kommer direkte ned ad symmetriaksen. I normal praksis er de to ender af sekundæret forbundet sammen med en lang ledning, der forbliver langt væk fra torusen, men for at opretholde den absolutte aksiale symmetri forestilles hele apparatet at være inde i en perfekt ledende kugle med sekundærtråden “jordet” til indersiden af kuglen i hver ende. Sekundæret er lavet af modstandstråd, så der er ingen separat belastning. E-feltet langs det sekundære forårsager strøm i det sekundære (gule pile), der forårsager et B-felt omkring det sekundære (vist som blå ellipser). Dette B-felt fylder plads, inklusive inde i transformerkernen, så i sidste ende er der kontinuerligt ikke-nul B-felt fra det primære til det sekundære, hvis det sekundære ikke er åbent kredsløb. Krydsproduktet Fra e-feltet (hentet fra primære strømme) og B-feltet (hentet fra sekundære strømme) danner Poynting-vektoren, der peger fra det primære mod det sekundære.