Waw! Galois klinkt zeker als een uniek Genie!

Hoe is de Galoistheorie nog bekend?in 1843, 10 jaar na Galois’ dood, slaagde de briljante Franse wiskundige Joseph Liouville erin om enkele van Galois’ ideeën te begrijpen. Na nog 3 jaar werk publiceerde Liouville een artikel om ze uit te leggen. Maar Liouville ‘ s artikel was nog steeds te vergezocht voor andere wiskundigen om ervan te genieten en te begrijpen. Het duurde nog eens 24 jaar om een Franse wiskundige te vinden die uitstekend genoeg was om Galois beter te begrijpen en zijn ideeën helder te maken. Deze uitstekende wiskundige is Camille Jordan. In feite was Jordan ‘ s boek uit 1870 over de Galoistheorie zo goed geschreven dat de Duitse wiskundige Felix Klein het net zo leesbaar vond als een Duits boek!

Het was zeker een enorme boost. Maar het zou nog 82 jaar duren voordat de Grote Oostenrijkse wiskundige Emil Artin de Galoistheorie eindelijk zijn moderne vorm gaf, in 1942. Artin verdient veel credits. Terwijl Galois de visionair was die deze revolutie voorzag, is Artin in vele opzichten degene die de revolutie ondernam en de wiskunde omver wierp. Dankzij Artin, en een paar anderen, is de Galoistheorie vandaag de dag een onvermijdelijke hoeksteen geworden van het onderzoek in de wiskunde, met tal van verrassende en verbazingwekkende prestaties (zoals Wiles’ bewijs van Fermat ‘ s laatste stelling), evenals een enorm reservoir van open vragen en mysteries!

velden in de zuivere Algebra

Galoistheorie gaat over symmetrieën van getallen. Maar voordat ik daar kom, moet ik je voorstellen om je bewapend te krijgen door je een geheim over getallen te vertellen. En ik weet zeker dat je ervan gehoord hebt! Inderdaad, op de middelbare school, werd je waarschijnlijk geleerd om nooit wortels achter te laten in de noemers.

Ik bedoel dat $1 / (\sqrt{2}-1)$ geen juist antwoord was. Kun je helpen om zich te ontdoen van de vierkantswortel van 2 in de noemer?

Hehe… we werden geleerd om op en neer te vermenigvuldigen met de conjugaat van de noemer. Dit conjugaat wordt verkregen door $-$ te vervangen door $ + $ (of vice versa) in de noemer:

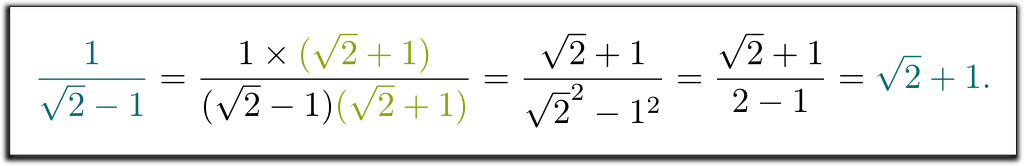
Ik weet het! De gecompliceerde uitdrukking $1 / (\sqrt{2}-1)$ vertegenwoordigt hetzelfde getal als $\sqrt{2}+1$. En dat verklaart waarom onze leraren wilden dat we resultaten op de ene manier schrijven in plaats van op de andere: als alles op dezelfde manier wordt geschreven, worden examens veel gemakkelijker te corrigeren!

maar hoe zit het met $1 / (\sqrt{2}-1)$? Kun je je ontdoen van de wortel in de noemer? Kan het wel?

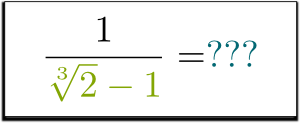
Ik weet het!

zeg het maar!

enig geluk?

Hehe … interessant is dat elke macht van $\sqrt{2}-1$ kan worden geschreven als een som van machten van $\sqrt{2}$. Inderdaad, u hoeft alleen maar de producten te distribueren:

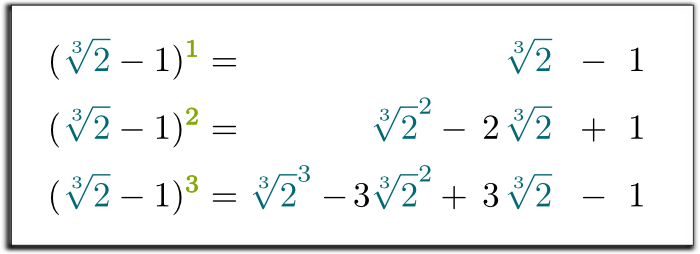
Ja dat is het! Door deze substitutie in de derde vergelijking te doen, hebben we aangetoond dat de drie eerste machten van $\sqrt{2}-1$ kunnen worden geschreven als een som van een rationeel getal, van $\sqrt{2}$ en van $\sqrt{2}^2$!

dus we hebben nu 3 vergelijkingen, met 2 root expressies die we kwijt willen! Zo kunnen we de vergelijkingen combineren om alle hoofduitdrukkingen aan de rechterkant te verwijderen!

laten we de 2 eerste regels vermenigvuldigen met 3 en alle 3 vergelijkingen optellen:

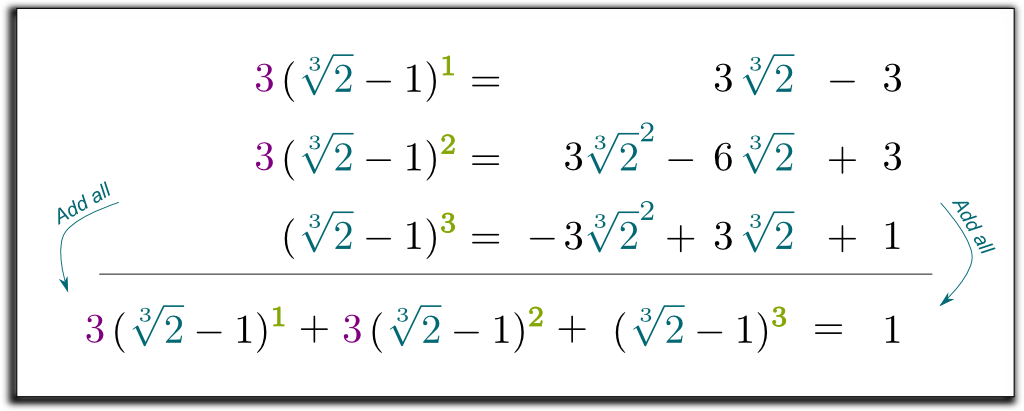
Hehe… het leuke is dat de linker term die we hebben verkregen nu kan worden ontbonden door $\sqrt{2}-1$! Laat me wat saaie berekeningen overslaan … en het resultaat $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Dus, om van de wortels in de noemer af te komen, kunnen we op en neer vermenigvuldigen met $\sqrt{2}^2 + \sqrt{2} + 1$! Tot slot krijgen we de volgende verrassende en mooie formule:

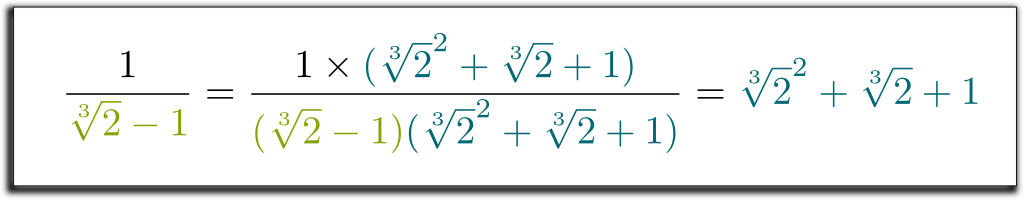
Ik weet het! Maar wat nog netter is, is dat de methode die we gebruikten zeer algemeen is! Met vergelijkbare technieken kunnen we nu alle radicalen uit noemers verwijderen!

wat voor Galois van bijzonder belang was, was niet het feit dat een methode het mogelijk maakte om radicalen uit noemers te verwijderen. Maar eerder, dat elk getal met radicalen in noemers gelijk aan een getal met radicalen op de top. Dit betekende dat de aantallen met radicalen bovenaan stabiel waren per verdeling.

het is gebruikelijk om $\mathbb Q{2}]$ aan te duiden de verzameling getallen die kan worden geschreven als een som van machten van $\sqrt{2}$. Omdat $\sqrt{2}^3 = 2$ een rationeel getal is, kan elke som van machten van $\sqrt{2}$ in feite worden geschreven in de standaardvorm $a \ sqrt{2}^2 + b \ sqrt{2} + c$. Nu, als je twee van zulke getallen optelt, aftrekt of vermenigvuldigt, dan is het niet zo moeilijk om te zien dat we getallen krijgen die nog steeds in de standaardvorm $a\sqrt{2}^2 + b\sqrt{2} + c$kunnen worden gezet. Plus, wat we hier zojuist hebben laten zien is dat de inverse van alle getallen $a\sqrt{2}^2 + b\sqrt{2} + c$ ook in standaardvorm kan worden geschreven. Dit toont aan dat elke optelling, aftrekking, vermenigvuldiging en deling van getallen in $\mathbb Q{2}]$ een getal oplevert, dat in standaardvorm kan worden geschreven… en dus behoort tot $\mathbb Q{2}]$. In zuivere algebra termen is $ \ mathbb Q{2}]$ dus stabiel door de vier klassieke rekenkundige bewerkingen. Daarom noemen we het een veld.

geometrie van Velduitbreidingen

het veld waar u het meest bekend mee bent is waarschijnlijk de verzameling $\mathbb Q$ van rationale getallen. Andere voorbeelden van velden zijn de Verzamelingen $\mathbb R$ van reële getallen en de verzameling $\mathbb C$ van complexe getallen. En nu hebben we ook $\mathbb Q{2}]$. Omdat $ \ mathbb Q{2}]$ een veld is dat het veld $\mathbb Q$ bevat, zeggen we dat $\mathbb Q{2}] / \mathbb Q$ Een veld extensie is.

het feit dat $ \ mathbb Q{2}] / \ mathbb Q$ Een velduitbreiding is, geeft een zeer natuurlijke verbinding tussen de twee velden. Namelijk, $ \ mathbb Q{2}]$ kan worden gezien als een vectorruimte, waar $\mathbb Q$ het scalaire veld is. In het bijzonder, het feit dat een getal in $\mathbb Q{2}]$ kan worden geschreven $a \sqrt{2}^2 + b\sqrt{2} + c$ betekent dat $(1, \sqrt{2}, \sqrt{2}^2)$ een basis vormt van $\mathbb Q{2}]$ als een $\mathbb Q$-vectorruimte. En dit betekent dat we het geometrisch kunnen representeren als een 3-dimensionale ruimte!

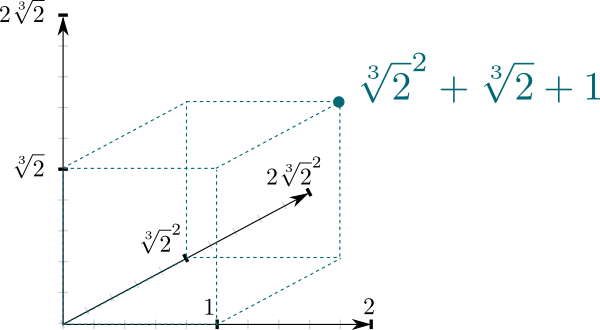
De dimensie van de vectorruimte hierboven is een interessante eigenschap van velduitbreidingen. Het staat bekend als de graad, en het wordt meestal aangeduid $\big{2}] : \mathbb Q\big] = 3$ bijvoorbeeld.

Ja! Het is eigenlijk vrij eenvoudig om hier een veldextensie van te maken: voeg gewoon een radicaal getal toe dat niet bij $\mathbb Q{2}]$hoort!

Ja! Hiermee wordt het veld $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$aangemaakt. Deze velden bevatten alle getallen die producten zijn en sommen van $\sqrt{2}$ en $\sqrt{2}$. Deze zijn van de vorm $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} $ + $ f \sqrt{2}$. Enig idee wat de graad $ \ big{2}, \ sqrt{2}]: \ mathbb Q{2}] \ big]$ is?

Ja! Inderdaad, we hebben $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e \sqrt{2} + F) \sqrt{2}$. Dus kan elk getal van $ \ mathbb Q{2},\sqrt{2}]$ worden geschreven $A+B \ sqrt{2}$, waarbij $A$ en $B$ behoren tot $ \ mathbb Q{2}]$. Zo bepalen 2 scalars van $\mathbb Q{2}]$ een getal in $ \ mathbb Q{2},\sqrt{2}]$. Dit betekent dat de graad van de velduitbreiding $ \ mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ 2 is. In feite hebben we de relatie tussen Chasles $\big{2}, \sqrt{2}]: \ mathbb Q \ big] $ = $ \big{2}, \sqrt{2}] : \mathbb Q{2}] \big] \ big{2}]: \mathbb Q \ big] $ = $ 2 \times 3 = 6$.

Het is beter dan dat! Elke velduitbreiding van eindige graad, genaamd eindige velduitbreiding, wordt overspannen door een enkele getallen. Bijvoorbeeld $ \ mathbb Q{2}, \sqrt{2}] $ = $ \ mathbb Q{2} + \sqrt{2}]$, Wat betekent dat alle getallen die sommen van machten van $\sqrt{2}$ en $\sqrt{2}$ zijn ook sommen van machten van $\sqrt{2} + \sqrt{2}$zijn. Is het niet verrassend geweldig?

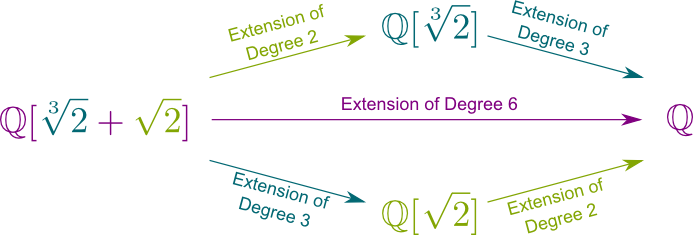
meer in het algemeen kan elke eindige veldextensies van $\mathbb Q$ worden geschreven $\mathbb Q$ met ongeveer $x$ die wordt toegevoegd aan $\mathbb Q$.

Ja. Het is het geval voor de veld extensie $ \ mathbb R / \ mathbb Q$. En, zo is de belangrijkste velduitbreiding in de Galoistheorie! Deze velduitbreiding is $ \ bar {\mathbb Q} / \ mathbb Q$, waarbij $ \ bar {\mathbb Q}$ de verzameling van algebraïsche getallen is. Dit zijn allemaal oplossingen voor veeltermvergelijkingen van de vorm $a_n x^n $+$ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $+$ a_0 = 0$. Bijvoorbeeld, $\sqrt{2}$ is een algebraïsch getal omdat het een oplossing is voor $x^4-2x = 0$. $ \ Bar {\mathbb Q}$ is dus een velduitbreiding voor alle eindige velduitbreidingen van $ \ mathbb Q$.

geconjugeerde getallen

We zijn er bijna! We hebben een laatste omweg nodig door polynomiale vergelijkingen.

precies! Galois merkte op dat sommige vergelijkingen vereenvoudigd konden worden. Bijvoorbeeld, $x^4-2x = 0$ kan worden gefactoriseerd als $x(x^3-2)=0$, wat overeenkomt met $x=0$ of $x^3-2 = 0$. Dus, de vergelijking $x^4-2x = 0$ kan worden gereduceerd tot vergelijkingen $x=0$ en $X^3-2=0$. En in feite is deze reductie zeer vergelijkbaar met hoe getallen als 35 kunnen worden gereduceerd tot 5 en 7, omdat $5 \ keer 7 = 35$. De gelijkenis tussen vergelijkingen en hele getallen is zo sterk dat we zelfs Euclidische verdelingen van veeltermen kunnen maken, net zoals je dat Voor getallen hebt geleerd! Aan de rechterkant is een voorbeeld van een dergelijke verdeling (maak je geen zorgen als je het niet begrijpt, het zal niet belangrijk zijn voor het vervolg).

precies! Deze zijn bekend als irreducible polynomiale vergelijkingen. De vergelijking $x^3-2 = 0$ is een voorbeeld van irreducible veeltermvergelijking.

Ja! Maar, cruciaal, Galois wilde zich richten op vergelijkingen met rationele coëfficiënten. Of beter gezegd, veeltermen met coëfficiënten die tot het basisveld behoren. Dus, wat ik bedoelde was dat, Voor $ \ mathbb Q$ Als het basisveld, $x^3-2 = 0$ onherleidbaar is.

laten we $x^2 – 2x -1=0$ beschouwen als enige aanwijzingen. Deze vergelijking kan worden bewezen onherleidbaar te zijn. Weet je nog hoe je het moet oplossen?

als $b^2-4ac \ geq 0$, Ja.

precies! Dus de onherleidbare veeltermvergelijking $x^2 + 2x -1 = 0$ heeft twee oplossingen: $1+\sqrt{2}$ en $1-\sqrt{2}$ … enig commentaar?

Bingo! Dat is de belangrijkste ontdekking van Galois. Meer in het algemeen, Galois genoemd conjugeert alle oplossingen aan een irreducible veeltermvergelijking. En, zoals je je kunt voorstellen, deze zijn essentieel om radicalen uit noemers te verwijderen!

het eerste wat opvalt is dat als $x_1$, $x_2$, …, $x_n$ alle oplossingen zijn van een polynoom irreducible vergelijking $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ met rationale coëfficiënten, dan kan deze polynoom irreducible vergelijking eigenlijk worden herschreven $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Het identificeren van de constante termen levert dan $x_1 x_2 … x_n $ = $ (-1)^n a_0/a_n$op. Dus, cruciaal, het product van geconjugeerde getallen is het rationele getal $(-1)^n a_0 / a_n$, dat niet-nul is (bewijs het!).

Hier is een grapje om de sterke verbinding tussen conjugaten in gedachten te houden:

beschouw een breuk $1/x_1$, waarbij $x_1$ een gecompliceerde uitdrukking is met radicalen. Op en neer vermenigvuldigen met de conjugaten $x_2$,…, $x_n$ van $x_1$ geeft dan $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, die geen radicaal heeft in de noemer omdat we $a_0$ hebben vastgesteld als een niet-nul getal van het basisveld!

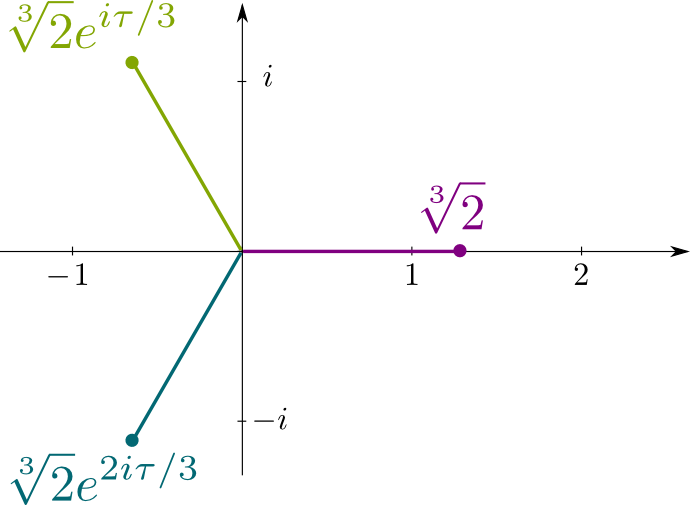
bedenk dat $x^3-2 = 0$ de onherleidbare veeltermvergelijking is $\sqrt{2}$ is de oplossing van. Dus, zijn conjugaten zijn de andere oplossingen voor die vergelijking, die de complexe getallen $\sqrt{2}j$ en $\sqrt{2}j^2$ zijn, waarbij $j= e^{i\tau/3}$ met $\tau = 2\pi$ de verhouding is van de omtrek van een cirkel door zijn straal. De volgende figuur toont de locaties van de geconjugeerde oplossingen in dit complexe vlak:

Galois’ ambiguïteit

eindelijk krijgen we Galois ‘ sleutelinzicht!

conjugaten zijn perfect permuteerbaar. Dit betekent dat, als je systematisch $\sqrt{2}$ verandert door zijn geconjugeerde $-\sqrt{2}$, dan gelden nog steeds gelijkenissen. Bijvoorbeeld, omdat we $1/(\sqrt{2}-1) = \sqrt{2}+1$ hadden, Kan ik je direct vertellen dat $1 / (- \sqrt{2}-1)= – \sqrt{2}+1$! Evenzo hebben we de volgende verbluffende implicatie:

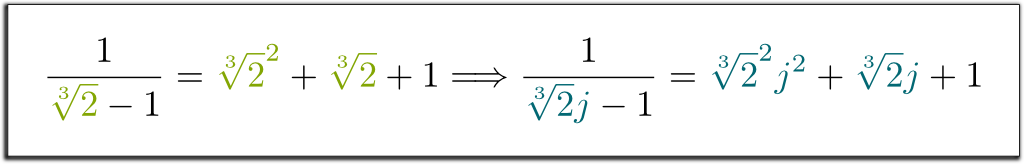
Hehe … laat me eerst herinneren dat eindige velden worden overspannen door een enkel element. Dus, als het basisveld $\mathbb Q$ is, kan elk eindig veld $\mathbb Q$ worden geschreven voor een recht $x_1$. Overweeg nu $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ de onherleidbare veeltermvergelijking $x_1$ is de oplossing van. Dan, wat $\mathbb Q $ definieert is de$ \ mathbb Q $-vectorruimte overspannen door$ x_1$,$ x_1^2$,…,$ x_1^{n-1}$, met de vereenvoudiging van grotere bevoegdheden van$ x_1 $overeenkomstig de algebraïsche regel $ x_1^n $ = $ – a_{n-1}x_1^{n-1} $ – $ … – a_0$.

precies! Cruciaal is dat deze algebraïsche regels van $ \ mathbb Q$ niet echt afhangen van de aard van $x_1$; ze hangen alleen af van de onherleidbare veelterm $x_1$ is de oplossing van! Daarom zijn de regels van $ \ mathbb Q$ identiek aan die van $ \ mathbb Q$,…, $ \ mathbb Q$, Waar $x_1$ wordt vervangen door een van zijn conjugaten $x_2$, …, $x_n$. In het bijzonder werken de velden $\mathbb Q{2}]$ en $\mathbb Q{2} j]$ overeenkomstig exact dezelfde regels. Daarom zijn conjugaten perfect permuteerbaar! We zeggen dat de velden $ \ mathbb Q{2}]$ en $ \ mathbb Q{2} j]$ isomorf zijn, en dat het vervangen van $\sqrt{2}$ door $\sqrt{2}j$ een isomorfisme is $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

op een zeer vergelijkbare (maar sterkere) manier dat twee vectorruimten van Dimensie 2 min of meer hetzelfde zijn! Dit heeft een verschrikkelijk gevolg. Het betekent dat, vanuit een algebraïsch perspectief, het zinloos is om een verschil te maken tussen een getal en een van zijn conjugaten (zolang je het getal systematisch vervangt door zijn conjugaat)! Dus, bijvoorbeeld, $\sqrt{2}$ en $ – \sqrt{2}$ zijn algebraïsch niet te onderscheiden! Om dit in gedachten te houden, Hier is een andere grap die ik heb bedacht:

helemaal niet! Elk onderscheid tussen deze twee getallen moet betrekking hebben op een andere wiskunde dan de algebra, zoals orde relaties of topologie. Wat ik bedoel is dat bijvoorbeeld de relatie $\sqrt{2} > 0$ een verschil maakt tussen $\sqrt{2}$ door $-\sqrt{2}$, maar dat komt omdat het een orderrelatie betreft. Maar als we ons beperken tot polynomiale gelijkenissen, dan is er absoluut geen verschil tussen $\sqrt{2}$ en $-\sqrt{2}$. Op dezelfde manier zijn $i$ en $-i$, de oplossingen van de onherleidbare veeltermvergelijking $x^2+1=0$, ook algebraïsch niet te onderscheiden. Toch noemen we willekeurig $i$ een van hen. Daarom noemde Galois zijn theorie de theorie van ambiguïteit. Tegenwoordig wordt de dubbelzinnigheid van de keuze van de conventionele vierkantswortel van $-1$ tussen $i$ en $-i$ eerder de symmetrie tussen $i$ en $-i$genoemd.

Galois-groepen

Galois richtte zich vooral op velduitbreidingen die stabiel zijn door conjugatie. Dergelijke stabiele veldextensies staan nu bekend als Galois-extensies. Dus, als $x_1$ bij een Galois extensie hoort, dan bevat deze Galois extensie alle conjugaten $x_2$,…, $x_n$.

een eenvoudige manier om galoisuitbreidingen te construeren bestaat uit het nemen van het veld dat wordt overspannen door oplossingen van een onherleidbare veeltermvergelijking. Bijvoorbeeld, als $x_1$,…, $x_n$ conjugaten zijn voor het basisveld $ \ mathbb Q$, dan is $ \ mathbb Q / \ mathbb Q$ Een Galois extensie. Op deze manier geconstrueerde velden worden splitsingsvelden genoemd.

bijvoorbeeld, het splitsingsveld van vergelijking $x^3-2=0$ is de Galois-extensie $ \ mathbb Q{2}, \ sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ overspannen door zijn oplossingen.

als $x_1$ een Galois extensie overspant, dan doen de conjugaten dat ook. Dus, $ \ mathbb Q = \ mathbb Q = $ … $=\mathbb Q$ = $ \ mathbb Q$. Dus het isomorfisme tussen $ \ mathbb Q$ en $ \ mathbb Q$ dat bestaat in het altijd vervangen van $x_1$ door $x_2$ is in feite een isomorfisme tussen $\mathbb Q$ en zichzelf! We noemen het een automorfisme. Automorfismen van een Galois extensie $ \ mathbb Q / \ mathbb Q$ vormen de Galois groep $Gal (\mathbb Q/ \ mathbb Q)$.

nu, cruciaal, als $ \ mathbb Q = \ mathbb Q$, dan zijn alle automorfismen van een Galois extensie $ \ mathbb Q / \ mathbb Q$ permutaties van $x_1$ met een van zijn conjugaten! In het bijzonder zien we hier dat de kardinaliteit van een Galoisgroep gelijk is aan de graad van de galoisuitbreiding.

zeker! Je kunt zien dat $ \ mathbb Q = \ mathbb Q$ en $\mathbb Q = \ mathbb Q$, Wat betekent dat $i$ en $\sqrt{2}$ Elk de splitsingsvelden van de irreducible veeltermvergelijking omvatten waar ze de oplossing van zijn. Dus, $ \ mathbb Q/\mathbb Q$ en $\mathbb Q / \ mathbb Q$ Zijn beide Galois extensies. Daarom bestaan hun automorfismen uit het vervangen van $i$ door een van zijn conjugaten, $i$ of $-i$, en het vervangen van $\sqrt{2}$ door $\sqrt{2}$ of $-\sqrt{2}$. In de eerste gevallen veranderen we niets in getallen, wat overeenkomt met de nulsymmetrie. De tweede gevallen kunnen worden gevisualiseerd als axiale symmetrieën, zoals weergegeven in de onderstaande figuur:

is dat niet verbazingwekkend?

zeker! Laten we naar het splitsingsveld $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2]$ van $x^3-2=0$. Maar, voordat we verder gaan, laten we opmerken dat $ \ mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \ mathbb Q{2}, j]$.

alles wat we moeten bewijzen is dat alle generatoren van het ene veld bij het andere horen. Laten we beginnen met te bewijzen dat de generatoren van de laatste, $\sqrt{2}$ en $j$, tot de eerste behoren. Het is duidelijk voor $\sqrt{2}$. Nu, $j = (\sqrt{2} j) / \sqrt{2}$, dus $j$ behoort ook tot het voormalige veld. Dit bewijst dat alle elementen van $ \ mathbb Q{2}, j]$ behoren tot $ \ mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Omgekeerd is het eenvoudig dat alle generatoren van het eerste veld, $\sqrt{2}$, $\sqrt{2}j$ en $\sqrt{2}j^2$, producten zijn van de generatoren van het laatste veld. Beide velden zijn dus gelijk. En, in het bijzonder, $\mathbb Q{2}, j]/\mathbb Q$ is een Galois extensie.

Hehe … om de symmetrieën van $\mathbb Q{2}]$ te begrijpen, moeten we verder gaan in Galois’ studie van Galoisgroepen…

Galoiscorrespondentie

Het Probleem met Galoisgroepen is dat ze extreem groot en ingewikkeld kunnen worden. Dit is in het bijzonder het geval van de oneindige groep $Gal(\bar{\mathbb Q}/\mathbb Q)$. Om zulke grote en complexe groepen te begrijpen, had Galois het briljante idee om deze in kleinere stukken te breken.

verbazingwekkend genoeg ontdekte Galois dat Galoisgroepen konden worden opgesplitst in subgroepen van symmetrieën door alleen te kijken naar die groepen die een deelveld onveranderd laten. Bijvoorbeeld, $ \ mathbb Q$ is een subveld van $ \ mathbb Q{2}, j]$, omdat elk getal van de eerste tot de laatste behoort. Symmetrieën van $ \ mathbb Q{2}, j]$ die niets veranderen aan $\mathbb Q$ vormen dus een subgroep van de Galoisgroep van $ \ mathbb Q{2},j]/\mathbb Q$. Deze symmetrieën vormen de Galoisgroep $Gal (\mathbb Q{2},j]/ \ mathbb Q)$.

Ik weet het! Ik visualiseer deze symmetrieën graag als de manieren om $\mathbb Q{2},j]$ aan te sluiten op $ \ mathbb Q$. Hier is een afbeelding van het “pluggen op”:

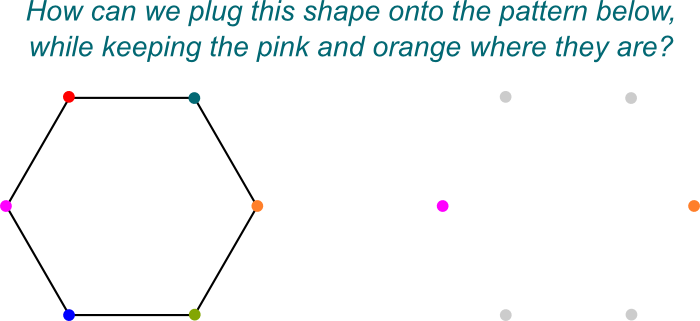
precies! En dat is simpelweg omdat $ \ mathbb Q{2}, j]$ een Galois extensie is van $ \ mathbb Q$ Wat zelf een veld extensie is van $ \ mathbb Q$.

en er is meer! Galois toonde aan dat alle subgroepen van een Galois extensies op deze manier verkregen worden! Meer precies, de toewijzing van elk veld $K$ tussen de Galois extensie $ \ mathbb Q{2}, j]$ en het basisveld $\mathbb Q$ aan de Galois groep $Gal(\mathbb Q{2},j] / K)$ is bijectief. Dit feit wordt de Galois correspondentie genoemd! Deze correspondentie wordt hieronder schematisch weergegeven voor een Galois extensie $ \ mathbb Q / \ mathbb Q$.

in plaats van deze groep direct te beschrijven, laten we ons concentreren op de subgroep $Gal(\mathbb Q{2}, j]/\mathbb Q)$. Het is duidelijk dat $\sqrt{2}$ $overspant $ \ mathbb Q{2}, j]$ wanneer toegevoegd aan $ \ mathbb Q$. Dus, $ \ mathbb Q{2}, j] / \mathbb Q$ is een Galois extensie overspannen door $ \ sqrt{2}$. Daarom, met behulp van een stelling die we eerder gezien hebben, weten we dat alle automorfismen van deze Galois extensie bestaan in het vervangen van $\sqrt{2}$ door een van zijn 3 conjugaten (zelf, $\sqrt{2} j$ en $\sqrt{2} j^2$)!

nu zou ik andere stukken van $Gal(\mathbb Q{2}, j]/\mathbb Q)$ kunnen blijven bestuderen, zoals de Galois-subgroep $Gal (\mathbb Q{2},j]/\mathbb Q{2}])$. Maar Ik gebruik liever een andere van Galois’ krachtige stellingen. Namelijk, hij bewees dat als $ \ mathbb Q / \ mathbb Q$ bovendien een Galois extensie zelf was, dan is de subgroep $Gal(\mathbb Q{2}, j]/\mathbb Q)$ normaal.

dus, de Galoisgroep van $ \ mathbb Q{2}, j] / \ mathbb Q$ kan door deze subgroep worden quotiënteerd, en de quotiëntgroep is dan gelijk aan $Gal(\mathbb Q/\mathbb Q)$. Toch is $ \ mathbb Q / \ mathbb Q$ inderdaad een Galois extensie overspannen door $j$, waarvan het conjugaat $j^2$is. Dus, $Gal (\mathbb Q/ \ mathbb Q)$ bestaat uit het verlaten van $j$ als $j$ of het vervangen door $j^2$.

We kunnen nu alle symmetrieën van $Gal(\mathbb Q{2},j]/\mathbb Q)$ afleiden door deze van $Gal(\mathbb Q{2},j] / \mathbb Q)$ en $Gal(\mathbb Q/\mathbb Q)$te combineren. We kunnen deze symmetrieën weergeven door te tekenen hoe ze onze drie overspannende conjugaten beïnvloeden $\sqrt{2}$, $\sqrt{2}j$ en $\sqrt{2}j^2$:

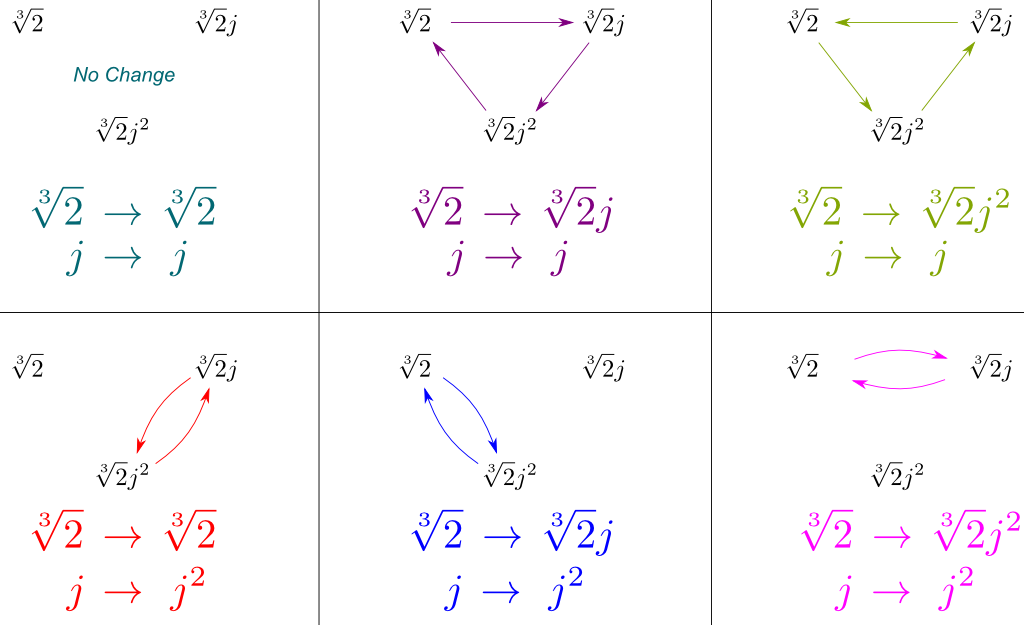
cruciaal is dat de figuur hierboven alle symmetrieën bevat van $Gal (\mathbb Q{2},j]/ \ mathbb Q)$. Verbazingwekkend genoeg komen deze symmetrieën overeen met de bekende symmetriegroep.

Ik laat Marcus du Sautoy het aan u presenteren:

dus, zijn symmetrieën hier als een zeester of als een driehoek?

Ja, inderdaad! Deze groep van symmetrieën van de driehoek wordt $D_3$ genoemd, en het is hetzelfde als de groep $S_3$ van permutaties van 3 elementen. Dit leidt ons naar de volgende formule, die ik zo mooi vond, dat ik heb besloten om het te framen!

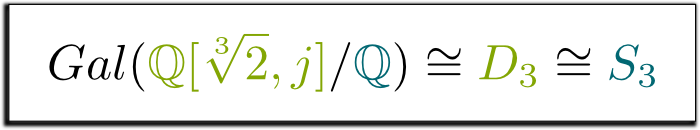
laten we concluderen

in veel opzichten moet Galois worden beschouwd als de vader van de moderne algebra. Zijn belangrijkste inzicht was om te kijken naar de wiskunde door de hoek van de regels van de operaties, en dit leidde hem tot het onthullen van verrassende en inzichtelijke dubbelzinnigheden, of symmetrieën, tussen getallen. Vanuit een algebraïsch perspectief zijn getallen als $\sqrt{2}$, $\sqrt{2}j$ en $\sqrt{2}j^2$ inderdaad volkomen symmetrisch en volledig uitwisselbaar.

het begrijpen van deze symmetrieën heeft verbazingwekkende toepassingen gehad in onder andere de algebraïsche meetkunde en de algebraïsche topologie. In het bijzonder omvatten vroege successen van de theorie een classificatie van construeerbare regelmatige veelhoeken en een stelling die beweert dat hoge graad veeltermvergelijkingen niet door radicalen konden worden opgelost.

recente successen verschijnen in de cryptografie en Andrew Wiles’ bewijs van Fermat ‘ s laatste stelling. Dit bewijs omvat het bestuderen van de Galoisgroep $Gal (\bar {\mathbb Q} / \ mathbb Q)$ met groepsrepresentatie. Maar ik zou zeggen dat de theorie nog jong is, en dat er nog veel te ontdekken valt. Het is immers een van de meest actieve onderzoeksgebieden in het hedendaagse pure wiskundeonderzoek.

Dit zou ons ertoe moeten leiden om nog veel meer eerbetuigingen te betalen aan Galois ‘ ongelooflijke Genie… laat me er een van SocraticaStudios opnemen.