8.2: The Wavefunctions
Die Lösungen für die Schrödinger-Gleichung des Wasserstoffatoms sind Funktionen, die Produkte einer sphärischen harmonischen Funktion und einer radialen Funktion sind.
\
Die Wellenfunktionen für das Wasserstoffatom hängen von den drei Variablen r, \(\theta\) und \(\varphi \) und den drei Quantenzahlen n, \(l\) und \(m_l\) ab. Die Variablen geben die Position des Elektrons relativ zum Proton in Kugelkoordinaten an. Das absolute Quadrat der Wellenfunktion, \(| \ psi (r, \ theta , \ varphi ) / ^ 2 \), ausgewertet bei \(r \), \ (\ theta \) und \(\varphi \) gibt die Wahrscheinlichkeitsdichte an, das Elektron in einem Differentialvolumen \(d \ tau \) zu finden, zentriert an der durch r, \(\ theta \) und \(\ varphi \) angegebenen Position.
Übung \(\pageIndex{1}\)
Was ist der Wert des Integrals
\
Die Quantenzahlen haben Namen: \ (n\) wird die Hauptquantenzahl genannt, \(l \) wird die Drehimpuls-Quantenzahl genannt, und \(m_l \) wird die magnetische Quantenzahl genannt, weil (wie wir in Abschnitt 8.4 sehen werden) die Energie in einem Magnetfeld hängt von \(m_l \) ab. Oft wird \(l\) die azimutale Quantenzahl genannt, weil sie eine Folge der \ (\theta\) -Gleichung ist, die den azimutalen Winkel \ (\Theta \) beinhaltet, der sich auf den Winkel zum Zenit bezieht.
Diese Quantenzahlen haben spezifische Werte, die durch die physikalischen Einschränkungen oder Randbedingungen der Schrödinger-Gleichung bestimmt werden: \(n\) muss eine ganze Zahl größer als 0 sein, \(l\) kann die Werte 0 bis n‑1 haben und \(m_l\) kann \(2l + 1\) Werte im Bereich von \(-l\) ‑ bis \(+l\) in einheiten- oder ganzzahligen Schritten haben. Die Werte der Quantenzahl \ (l\) werden normalerweise durch einen Buchstaben codiert: s bedeutet 0, p bedeutet 1, d bedeutet 2, f bedeutet 3; Die nächsten Codes werden alphabetisch fortgesetzt (z. B. g bedeutet \ (l = 4 \)). Die Quantenzahlen geben die Quantisierung physikalischer Größen an. Die diskreten Energien verschiedener Zustände des Wasserstoffatoms sind gegeben durch \(n \), die Größe des Drehimpulses ist gegeben durch \(l \), und eine Komponente des Drehimpulses (normalerweise von Chemikern als z‑Komponente gewählt) ist gegeben durch \ (m_l \). Die Gesamtzahl der Orbitale mit einem bestimmten Wert von \(n\) ist \(n ^ 2\).
Übung \(\pageIndex{2}\)
Betrachten Sie mehrere Werte für n und zeigen Sie, dass die Anzahl der Orbitale für jedes n \(n^2\) ist.
Übung \(\pageIndex{3}\)
Erstellen Sie eine Tabelle, die die zulässigen Werte für die Quantenzahlen n, \(l\) und \(m_l\) zusammenfasst. für die Energieniveaus 1 bis 7 Wasserstoff.
Übung \(\pageIndex{4}\)
Die Notation 3d gibt die Quantenzahlen für ein Elektron im Wasserstoffatom an. Was sind die Werte für n und \(l\)? Was sind die Werte für Energie und Drehimpuls? Was sind die möglichen Werte für die magnetische Quantenzahl? Was sind die möglichen Orientierungen für den Drehimpulsvektor?
Die Wasserstoffatom-Wellenfunktionen \(\psi (r, \theta , \varphi )\) werden Atomorbitale genannt. Ein Atomorbital ist eine Funktion, die ein Elektron in einem Atom beschreibt. Die Wellenfunktion mit n = 1, \ (l = 1 \) und \ (m_l \) = 0 wird als 1s-Orbital bezeichnet, und ein Elektron, das durch diese Funktion beschrieben wird, soll sich „im“ ls-Orbital befinden, d. H. Einen 1s-Orbitalzustand haben. Die Einschränkungen für \ (n \), \ (l) \) und \ (m_l \), die während der Lösung der Schrödinger-Gleichung des Wasserstoffatoms auferlegt werden, erklären, warum es ein einzelnes 1s-Orbital gibt, warum es drei 2p-Orbitale gibt, fünf 3d-Orbitale usw. Wir werden sehen, wenn wir Multielektronenatome in Kapitel 9 betrachten, dass diese Einschränkungen die Merkmale des Periodensystems erklären. Mit anderen Worten, das Periodensystem ist eine Manifestation des Schrödinger-Modells und der physikalischen Einschränkungen, die auferlegt werden, um die Lösungen der Schrödinger-Gleichung für das Wasserstoffatom zu erhalten.Die Visualisierung der Variation einer elektronischen Wellenfunktion mit \(r\), \(\theta\) und \(\varphi\) ist wichtig, da das absolute Quadrat der Wellenfunktion die Ladungsverteilung (Elektronenwahrscheinlichkeitsdichte) in einem Atom oder Molekül darstellt. Die Ladungsverteilung ist für die Chemie von zentraler Bedeutung, da sie mit der chemischen Reaktivität zusammenhängt. Beispielsweise wird ein elektronenarmer Teil eines Moleküls von einem elektronenreichen Bereich eines anderen Moleküls angezogen, und solche Wechselwirkungen spielen eine wichtige Rolle bei chemischen Wechselwirkungen, die von Substitutions- und Additionsreaktionen bis hin zur Proteinfaltung und der Wechselwirkung von Substraten mit Enzymen reichen.Die Visualisierung von Wellenfunktionen und Ladungsverteilungen ist eine Herausforderung, da das Verhalten einer Funktion von drei Variablen im dreidimensionalen Raum untersucht werden muss. Diese Visualisierung wird erleichtert, indem die radialen und eckigen Teile getrennt betrachtet werden, aber das separate Zeichnen der radialen und eckigen Teile zeigt die Form eines Orbital nicht sehr gut. Die Form kann in einem Wahrscheinlichkeitsdichtediagramm besser aufgedeckt werden. Um ein solches dreidimensionales Diagramm zu erstellen, teilen Sie den Raum in kleine Volumenelemente auf, berechnen Sie \ (\psi ^ * \psi \) in der Mitte jedes Volumenelements und schattieren, punktieren oder färben Sie dieses Volumenelement dann proportional zur Größe von \ (\psi^ * \ psi \). Verwechseln Sie solche Plots nicht mit polaren Plots, die ähnlich aussehen.
Wahrscheinlichkeitsdichten können auch durch Konturkarten dargestellt werden, wie in Abbildung \(\pageIndex{1}\) gezeigt.
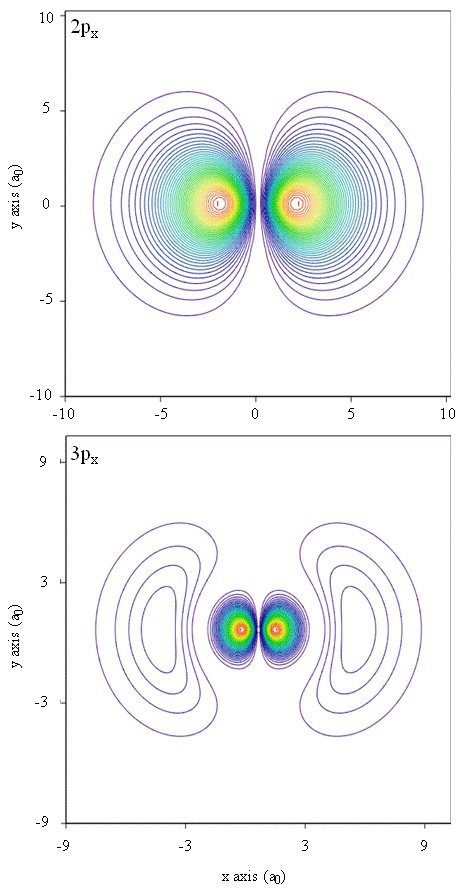
Eine weitere repräsentative Technik, die Modellierung der virtuellen Realität, ist vielversprechend für die Darstellung von Elektronendichten. Stellen Sie sich zum Beispiel vor, Sie könnten die Elektronendichte als Kraft oder Widerstand auf einem Zauberstab erfahren, den Sie durch den dreidimensionalen Raum bewegen. Geräte wie diese, sogenannte haptische Geräte, existieren bereits und werden zur Darstellung wissenschaftlicher Informationen eingesetzt. Wäre es nicht interessant, durch ein Atomorbital zu „fliegen“ und Änderungen der Elektronendichte als Farbänderungen oder Trübungsänderungen zu erfahren? Speziell gestaltete Räume mit 3D-Bildschirmen und „intelligenten“ Brillen, die Rückmeldung über die Blickrichtung des Betrachters geben, werden derzeit entwickelt, damit wir solche Empfindungen erleben können.
Methoden zur getrennten Untersuchung der radialen Anteile von Atomorbitalen liefern nützliche Informationen über die Verteilung der Ladungsdichte innerhalb der Orbitale. Graphen der Radialfunktionen \(R (r)\) für die 1s-, 2s- und 2p-Orbitale in Abbildung \(\pageIndex {2}\).
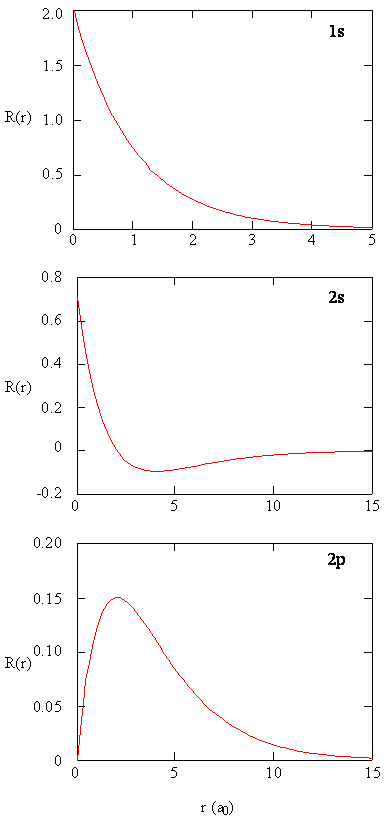
Die 1s-Funktion in Abbildung \(\pageIndex{2}\) beginnt mit einem hohen positiven Wert am Kern und fällt nach 5 Bohr-Radien exponentiell auf im Wesentlichen Null ab. Der hohe Wert im Kern mag überraschend sein, aber wie wir später sehen werden, ist die Wahrscheinlichkeit, ein Elektron im Kern zu finden, verschwindend gering.Beachten Sie als nächstes, wie die Radialfunktion für das 2s-Orbital, Abbildung \(\pageIndex{2}\), auf Null geht und negativ wird. Dieses Verhalten zeigt das Vorhandensein eines Radialknotens in der Funktion. Ein Radialknoten tritt auf, wenn die Radialfunktion gleich Null ist, außer bei \(r = 0\) oder \(r = ∞\). Knoten und Begrenzungsverhalten von Atomorbitalfunktionen sind beide nützlich, um zu identifizieren, welches Orbital durch welche Wellenfunktion beschrieben wird. Beispielsweise haben alle s-Funktionen Wellenfunktionswerte ungleich Null bei \ (r = 0\), aber p, d, f und alle anderen Funktionen gehen am Ursprung auf Null. Es ist nützlich, sich daran zu erinnern, dass es \ (n-1-l\) Radialknoten in einer Wellenfunktion gibt, was bedeutet, dass ein 1s-Orbital keine Radialknoten hat, ein 2s einen Radialknoten und so weiter.
Übung \(\pageIndex{5}\)
Untersuchen Sie die mathematischen Formen der radialen Wellenfunktionen. Welche Funktion in den Funktionen bewirkt, dass einige von ihnen am Ursprung auf Null gehen, während die s-Funktionen am Ursprung nicht auf Null gehen?
Übung \(\pageIndex{6}\)
Welches mathematische Merkmal jeder der Radialfunktionen steuert die Anzahl der Radialknoten?
Übung \(\pageIndex{7}\)
Bei welchem Wert von r tritt der 2s-Radialknoten auf?
Übung \(\pageIndex{8}\)
Erstellen Sie eine Tabelle, die die Energie, die Anzahl der Radialknoten und die Anzahl der Winkelknoten sowie die Gesamtzahl der Knoten für jede Funktion mit n = 1, 2 und 3 angibt. Identifizieren Sie die Beziehung zwischen der Energie und der Anzahl der Knoten. Identifizieren Sie die Beziehung zwischen der Anzahl der Radialknoten und der Anzahl der Winkelknoten.
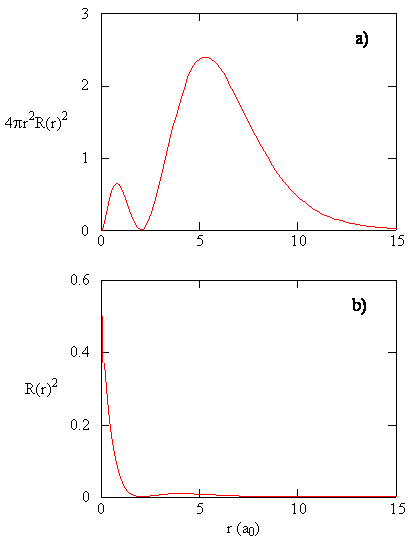
Die Größe \(R (r) ^* R(r)\) gibt die radiale Wahrscheinlichkeitsdichte an; d. H. Die Wahrscheinlichkeitsdichte, dass sich das Elektron an einem Punkt befindet, der in der Entfernung \(r\) vom Proton liegt. Radiale Wahrscheinlichkeitsdichten für drei Arten von Atomorbitalen sind in Abbildung (\pageIndex {3} \) dargestellt.
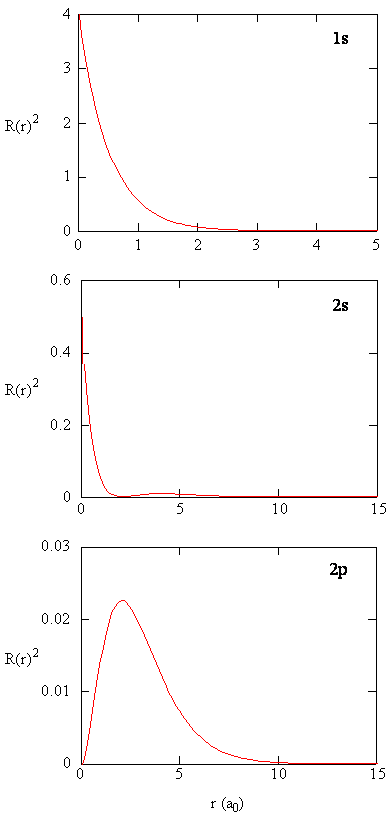
Wenn die radiale Wahrscheinlichkeitsdichte für jeden Wert von r mit der Fläche der sphärischen Oberfläche multipliziert wird, die durch diesen bestimmten Wert von r dargestellt wird, erhalten wir die radiale Verteilungsfunktion. Die radiale Verteilungsfunktion gibt die Wahrscheinlichkeitsdichte an, mit der ein Elektron irgendwo auf der Oberfläche einer Kugel gefunden wird, die sich in einem Abstand r vom Proton befindet. Da die Fläche einer Kugelfläche \(4 \pi r^ 2\) ist, ist die radiale Verteilungsfunktion gegeben durch \(4 \pi r^ 2 R(r) ^ * R (r)\).
Radiale Verteilungsfunktionen sind in Abbildung \(\pageIndex{4}\) dargestellt. Bei kleinen Werten von r ist die radiale Verteilungsfunktion niedrig, da die kleine Oberfläche für kleine Radien den hohen Wert der radialen Wahrscheinlichkeitsdichtefunktion in der Nähe des Kerns moduliert. Wenn wir \(r\) erhöhen, nimmt die mit einem gegebenen Wert von r verbundene Oberfläche zu, und der Term \ (r ^ 2\) bewirkt, dass die radiale Verteilungsfunktion zunimmt, obwohl die radiale Wahrscheinlichkeitsdichte abnimmt. Bei großen Werten von \ (r\) überwiegt der exponentielle Zerfall der Radialfunktion den durch den Term \ (r ^ 2 \) verursachten Anstieg, und die Radialverteilungsfunktion nimmt ab.
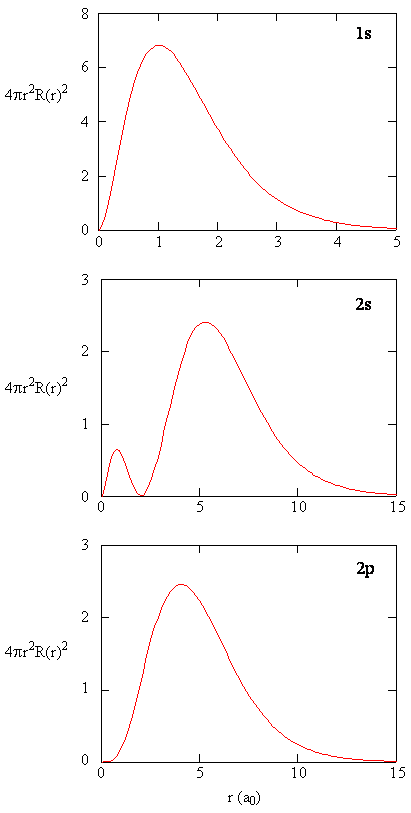
Übung \(\pageIndex{9}\)
Schreiben Sie einen Qualitätsvergleich der Radialfunktion und der Radialverteilungsfunktion für das 2s-Orbital. Siehe Abbildung (\pageIndex{5}\)
Mitwirkende und Zuschreibungen
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski („Quantenzustände von Atomen und Molekülen“)