Unter bestimmten Umständen trägt der Strom in der Wicklung einer Ringspule nur zum B-Feld innerhalb der Wicklungen bei und leistet keinen Beitrag zum magnetischen B-Feld außerhalb der Wicklungen. Dies ist eine Folge der Symmetrie und des Ampère-Schaltgesetzes.

Ausreichende Bedingungen für die vollständige interne Beschränkung des B-Feldesedit

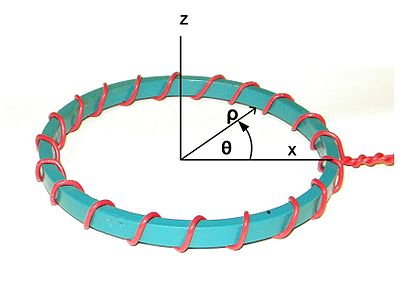1. Koordinatensystem. Die Z-Achse ist die nominelle Symmetrieachse. Die X-Achse willkürlich gewählt, um mit dem Startpunkt der Wicklung auszurichten. ρ wird als radiale Richtung bezeichnet. θ wird als Umfangsrichtung bezeichnet.

Abb. 2. Eine axialsymmetrische ringförmige Induktivität ohne Umfangsstrom.

Das Fehlen eines Umfangsstroms (der Weg des Umfangsstroms ist in Abbildung 3 dieses Abschnitts durch den roten Pfeil gekennzeichnet) und die axialsymmetrische Anordnung der Leiter und magnetischen Materialien sind ausreichende Bedingungen für die vollständige interne Begrenzung des B-Feldes. (Einige Autoren bevorzugen das H-Feld). Aufgrund der Symmetrie müssen die Linien des B-Flusses Kreise konstanter Intensität bilden, die auf der Symmetrieachse zentriert sind. Die einzigen Linien des B-Flusses, die einen Strom umgeben, sind diejenigen, die sich innerhalb der Ringwicklung befinden. Daher muss nach dem Ampere-Schaltgesetz die Intensität des B-Feldes außerhalb der Wicklungen Null sein.

Abb. 3. Ringspule mit Umfangsstrom

Abbildung 3 dieses Abschnitts zeigt die gebräuchlichste Ringwicklung. Es erfüllt beide Anforderungen für die vollständige B-Feldbeschränkung nicht. Von der Achse aus gesehen befindet sich die Wicklung manchmal auf der Innenseite des Kerns und manchmal auf der Außenseite des Kerns. Sie ist im Nahbereich nicht achsensymmetrisch. An Punkten mit einem Abstand von einem Vielfachen des Wicklungsabstands sieht der Toroid jedoch symmetrisch aus. Es gibt immer noch das Problem des Umfangsstroms. Egal wie oft die Wicklung den Kern umgibt und egal wie dünn der Draht ist, Dieser Ringkerninduktor enthält immer noch eine Spulenschleife in der Ebene des Ringkerns. Diese Wicklung erzeugt auch ein E-Feld in der Ebene des Induktors und ist dafür anfällig.

Die Abbildungen 4-6 zeigen verschiedene Möglichkeiten, den Umfangsstrom zu neutralisieren. Abbildung 4 ist die einfachste und hat den Vorteil, dass der Rücklaufdraht hinzugefügt werden kann, nachdem der Induktor gekauft oder gebaut wurde.

Abb. 4. Umfangsstrom konterte mit einem Rücklaufdraht. Der Draht ist weiß und verläuft zwischen dem äußeren Rand der Induktivität und dem äußeren Teil der Wicklung.

Abb. 5. Umfangsstrom mit einer Rückwicklung entgegengewirkt.

Abb. 6. Umfangsstrom mit einer geteilten Rückwicklung entgegengewirkt.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

Es wird eine Potentialverteilung entlang der Wicklung geben. Dies kann zu einem E-Feld in der Toroidebene und auch zu einer Suszeptibilität für ein E-Feld in der Toroidebene führen, wie in Abbildung 7 gezeigt. Dies kann durch die Verwendung einer Rücklaufwicklung gemildert werden, wie in Abbildung 8 gezeigt. Bei dieser Wicklung befinden sich die beiden Teile an jeder Stelle, an der sich die Wicklung kreuzt, auf gleicher und entgegengesetzter Polarität, was das in der Ebene erzeugte E-Feld erheblich verringert.

Toroidal inductor/transformer and magnetic vector potentialbearbeiten

Zeigt die Entwicklung des magnetischen Vektorpotentials um eine symmetrische Ringspule.

Siehe Feynman Kapitel 14 und 15 für eine allgemeine Diskussion des magnetischen Vektorpotentials. Siehe Feynman Seite 15-11 für ein Diagramm des magnetischen Vektorpotentials um einen langen dünnen Magneten, der auch eine vollständige innere Begrenzung des B-Feldes aufweist, zumindest in der unendlichen Grenze.

Das A-Feld ist genau, wenn die Annahme b f A = 0 {\displaystyle bf{A}=0}

. Dies würde unter den folgenden Annahmen zutreffen:

• 1. das Coulomb-Messgerät wird verwendet
• 2. die Lorenz-Lehre wird verwendet und es gibt keine Verteilung der Ladung, ρ = 0 {\displaystyle \rho =0\,}
  
• 3. das Lorenz-Messgerät wird verwendet und die Frequenz Null wird angenommen
• 4. das Lorenz-Messgerät wird verwendet und eine Frequenz ungleich Null, die niedrig genug ist, um 1 c 2 ∂ ϕ ∂ t {\displaystyle {\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}}
  

  zu vernachlässigen, wird angenommen.

Nummer 4 wird für den Rest dieses Abschnitts angenommen und kann als „quasi-statischer Zustand“ bezeichnet werden.

Obwohl die axialsymmetrische Ringspule ohne Umfangsstrom das B-Feld innerhalb der Wicklungen vollständig begrenzt, ist das A-Feld (magnetisches Vektorpotential) nicht begrenzt. Pfeil #1 im Bild zeigt das Vektorpotential auf der Symmetrieachse. Die radialen Stromabschnitte a und b sind gleich weit von der Achse entfernt, weisen jedoch in entgegengesetzte Richtungen, sodass sie sich aufheben. Ebenso brechen die Segmente c und d ab. Tatsächlich heben sich alle radialen Stromsegmente auf. Die Situation für axiale Ströme ist anders. Der axiale Strom an der Außenseite des Ringkerns ist nach unten gerichtet und der axiale Strom an der Innenseite des Ringkerns ist nach oben gerichtet. Jedes axiale Stromsegment an der Außenseite des Ringkerns kann mit einem gleichen, aber entgegengesetzt gerichteten Segment an der Innenseite des Ringkerns abgeglichen werden. Die Segmente auf der Innenseite sind näher als die Segmente auf der Außenseite an der Achse, daher gibt es eine Netto-Aufwärtskomponente des A-Feldes entlang der Symmetrieachse.

Darstellung der Felder des magnetischen Vektorpotentials (A), des magnetischen Flusses (B) und der Stromdichte (j) um eine ringförmige Induktivität mit kreisförmigem Querschnitt. Dickere Linien zeigen Feldlinien mit höherer durchschnittlicher Intensität an. Kreise im Querschnitt des Kerns stellen einen Fluss dar, der aus dem Bild kommt. Pluszeichen auf dem anderen Querschnitt des Kerns repräsentieren den B-Fluss, der ins Bild geht. Div A = 0 wurde angenommen.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ t → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

) die gleiche Form haben, dann beziehen sich die Linien und Konturen von A auf B wie die Linien und Konturen von B auf j. Somit ergibt sich eine Darstellung des A-Feldes um eine Schleife von B flux (wie sie in eine ringförmige Induktivität) ist qualitativ das gleiche wie das B-Feld um eine Stromschleife. Die Abbildung links ist eine künstlerische Darstellung des A-Feldes um einen ringförmigen Induktor. Die dickeren Linien zeigen Pfade mit höherer durchschnittlicher Intensität an (kürzere Pfade haben eine höhere Intensität, so dass das Pfadintegral gleich ist). Die Linien werden nur gezeichnet, um gut auszusehen und das allgemeine Aussehen des Feldes zu vermitteln.

Toroidal transformer action in presence of total B field confinementbearbeiten

Die Felder E und B können aus den Feldern A und ϕ {\displaystyle \phi \,}

(skalares elektrisches Potential) B = ∇ × A berechnet werden. {\displaystyle \mathbf {B} =\nabla \Zeiten \mathbf {A} .}

und : E = − ∇ ϕ − ∂ A ∂ t {\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}

und selbst wenn der Bereich außerhalb der Wicklungen kein B-Feld enthält, ist er mit einem E-Feld ungleich Null gefüllt. Die Größe ∂ A ∂ t {\displaystyle {\frac {\partial \mathbf {A} }{\partial t}}}

ist für die erwünschte Magnetfeldkopplung zwischen Primär und Sekundär verantwortlich, während die Größe ∇ ϕ {\displaystyle \nabla \phi \,}

ist für die unerwünschte elektrische Feldkopplung zwischen Primär und Sekundär verantwortlich. Transformatordesigner versuchen, die elektrische Feldkopplung zu minimieren. Für den Rest dieses Abschnitts wird ∇ ϕ {\displaystyle \nabla \phi \,}

als Null angenommen, sofern nicht anders angegeben.

Es gilt der Stokes-Satz, so dass das Pfadintegral von A gleich dem eingeschlossenen B-Fluss ist, so wie das Pfadintegral B gleich a konstant mal dem eingeschlossenen Strom ist

Das Pfadintegral von E entlang der Sekundärwicklung ergibt die induzierte EMK (Elektromotivkraft) der Sekundärwicklung.

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

was besagt, dass die EMK gleich die zeitliche Änderungsrate des von der Wicklung eingeschlossenen B-Flusses, was das übliche Ergebnis ist.

Ringkerntransformator Poynting Vektorkopplung von Primär zu Sekundär in Gegenwart von insgesamt B Feldbegrenzungbearbeiten

In dieser Abbildung zeigen blaue Punkte an, wo B vom Primärfeld zum Sekundärfeld fließt strom kommt aus dem Bild und Pluszeichen zeigen an, wo es ins Bild geht.

Erläuterung der figureEdit

Diese Abbildung zeigt den Halbschnitt eines Ringkerntransformators. Es werden quasistatische Bedingungen angenommen, so dass die Phase jedes Feldes überall gleich ist. Der Transformator, seine Wicklungen und alle Dinge sind symmetrisch um die Symmetrieachse verteilt. Die Wicklungen sind so, dass kein Umfangsstrom vorhanden ist. Die Anforderungen für eine vollständige interne Begrenzung des B-Feldes aufgrund des Primärstroms sind erfüllt. Der Kern und die Primärwicklung werden durch den graubraunen Torus dargestellt. Die Primärwicklung ist nicht dargestellt, aber der Strom in der Wicklung an der Querschnittsfläche ist als goldene (oder orange) Ellipsen dargestellt. Das durch den Primärstrom verursachte B-Feld ist vollständig auf den von der Primärwicklung umschlossenen Bereich (d. H. den Kern) beschränkt. Blaue Punkte auf dem linken Querschnitt zeigen an, dass Linien des B-Flusses im Kern aus dem linken Querschnitt herauskommen. Auf dem anderen Querschnitt zeigen blaue Pluszeichen an, dass der B-Fluss dort eintritt. Das E-Feld, das von den Primärströmen stammt, ist als grüne Ellipsen dargestellt. Die Sekundärwicklung ist als braune Linie dargestellt, die direkt entlang der Symmetrieachse verläuft. In der normalen Praxis sind die beiden Enden des Sekundärdrahtes mit einem langen Draht verbunden, der weit vom Torus entfernt ist, aber um die absolute axiale Symmetrie aufrechtzuerhalten, wird die gesamte Vorrichtung als innerhalb einer perfekt leitenden Kugel mit dem Sekundärdraht „geerdet“ an jedem Ende zur Innenseite der Kugel. Die Sekundärseite besteht aus Widerstandsdraht, sodass keine separate Last vorhanden ist. Das E-Feld entlang der Sekundärseite verursacht Strom in der Sekundärseite (gelbe Pfeile), der ein B-Feld um die Sekundärseite herum verursacht (als blaue Ellipsen dargestellt). Dieses B-Feld füllt den Raum, einschließlich innerhalb des Transformatorkerns, so dass am Ende ein kontinuierliches B-Feld ungleich Null von der Primär- zur Sekundärseite vorhanden ist, wenn die Sekundärseite nicht kurzgeschlossen ist. Das Kreuzprodukt des E-Feldes (aus Primärströmen) und des B-Feldes (aus Sekundärströmen) bildet den Poynting-Vektor, der vom Primär zum Sekundärvektor zeigt.