Todas las técnicas de regresión contienen una única variable de salida (respuesta) y una o más variables de entrada (predictor). La variable de salida es numérica. La metodología de construcción de árboles de regresión general permite que las variables de entrada sean una mezcla de variables continuas y categóricas. Se genera un árbol de decisiones cuando cada nodo de decisión del árbol contiene una prueba sobre el valor de alguna variable de entrada. Los nodos terminales del árbol contienen los valores de las variables de salida previstas.

Un árbol de regresión puede ser considerado como una variante de árboles de decisión, diseñado para aproximar funciones de valor real, en lugar de ser utilizado para métodos de clasificación.

Metodología

Un árbol de regresión se construye a través de un proceso conocido como particionamiento recursivo binario, que es un proceso iterativo que divide los datos en particiones o ramas, y luego continúa dividiendo cada partición en grupos más pequeños a medida que el método se mueve hacia arriba en cada rama.

Inicialmente, todos los registros del Conjunto de entrenamiento (registros preclasificados que se utilizan para determinar la estructura del árbol) se agrupan en la misma partición. El algoritmo comienza a asignar los datos en las dos primeras particiones o ramas, utilizando cada división binaria posible en cada campo. El algoritmo selecciona la división que minimiza la suma de las desviaciones cuadradas de la media en las dos particiones separadas. Esta regla de división se aplica a cada una de las ramas nuevas. Este proceso continúa hasta que cada nodo alcanza un tamaño de nodo mínimo especificado por el usuario y se convierte en un nodo terminal. (Si la suma de desviaciones cuadradas de la media en un nodo es cero, entonces ese nodo se considera un nodo terminal incluso si no ha alcanzado el tamaño mínimo.)

Poda del Árbol

Dado que el árbol se cultiva a partir del Conjunto de Entrenamiento, un árbol completamente desarrollado generalmente sufre de sobrecoste (es decir, está explicando elementos aleatorios del Conjunto de Entrenamiento que probablemente no sean características de la población más grande). Este ajuste excesivo da como resultado un rendimiento deficiente en los datos de la vida real. Por lo tanto, el árbol debe podarse utilizando el Conjunto de validación. XLMiner calcula el factor de complejidad de costos en cada paso durante el crecimiento del árbol y decide el número de nodos de decisión en el árbol podado. El factor de complejidad de costos es el factor multiplicativo que se aplica al tamaño del árbol (medido por el número de nodos terminales).

El árbol se poda para minimizar la suma de: 1) la varianza de la variable de salida en los datos de validación, tomados de un nodo terminal a la vez; y 2) el producto del factor de complejidad de costos y el número de nodos terminales. Si el factor de complejidad de costos se especifica como cero, entonces la poda es simplemente encontrar el árbol que funciona mejor en los datos de validación en términos de varianza total del nodo terminal. Los valores más grandes del factor de complejidad de costos dan como resultado árboles más pequeños. La poda se realiza sobre la base de la última entrada, la primera salida, lo que significa que el último nodo cultivado es el primero en ser eliminado.

Métodos de ensamble

XLMiner V2015 ofrece tres potentes métodos de ensamble para usar con árboles de regresión: embolsado (agregación de arranque), refuerzo y árboles aleatorios. El algoritmo de Árbol de Regresión se puede utilizar para encontrar un modelo que resulte en buenas predicciones para los nuevos datos. Podemos ver las estadísticas y matrices de confusión del predictor actual para ver si nuestro modelo se ajusta bien a los datos; pero ¿cómo sabremos si hay un mejor predictor esperando a ser encontrado? La respuesta es que no sabemos si existe un mejor predictor. Sin embargo, los métodos de conjunto nos permiten combinar múltiples modelos de árbol de regresión débiles, que cuando se toman juntos forman un nuevo modelo de árbol de regresión fuerte y preciso. Estos métodos funcionan creando múltiples modelos de regresión diversos, tomando diferentes muestras del conjunto de datos original y luego combinando sus resultados. (Los resultados pueden combinarse mediante varias técnicas, por ejemplo, el voto mayoritario para la clasificación y el promedio para la regresión) Esta combinación de modelos reduce efectivamente la varianza en el modelo fuerte. Los tres tipos de métodos de ensamble ofrecidos en XLMiner (embolsado, refuerzo y árboles aleatorios) difieren en tres elementos: 1) la selección del conjunto de entrenamiento para cada predictor o modelo débil; 2) cómo se generan los modelos débiles; y 3) cómo se combinan las salidas. En los tres métodos, cada modelo débil es entrenado en todo el Conjunto de Entrenamiento para ser competente en alguna parte del conjunto de datos.

Embolsado (agregación de bootstrap) fue uno de los primeros algoritmos de ensamble que se escribieron. Es un algoritmo simple, pero muy efectivo. El ensacado genera varios Conjuntos de entrenamiento mediante el uso de muestreo aleatorio con reemplazo (muestreo de arranque), aplica el algoritmo de árbol de regresión a cada conjunto de datos, luego toma el promedio entre los modelos para calcular las predicciones para los nuevos datos. La mayor ventaja de embolsar es la relativa facilidad con la que el algoritmo puede ser paralelizado, lo que lo convierte en una mejor selección para conjuntos de datos muy grandes.

Boosting construye un modelo sólido entrenando sucesivamente modelos para concentrarse en registros que reciben valores predichos inexactos en modelos anteriores. Una vez completados, todos los predictores se combinan por mayoría ponderada de votos. XLMiner ofrece tres variaciones de impulso implementadas por el algoritmo AdaBoost (uno de los algoritmos de conjunto más populares en uso hoy en día): M1 (Freund), M1 (Breiman) y SAMME (Modelado Aditivo por etapas utilizando un Exponencial de Múltiples clases).

Adaboost.M1 asigna primero un peso [wb (i)] a cada registro u observación. Este peso se establece originalmente en 1 / n, y se actualizará en cada iteración del algoritmo. Se crea un árbol de regresión original utilizando este primer Conjunto de entrenamiento (Tb) y se calcula un error como

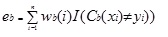
donde, la función I () devuelve 1 si es verdadero y 0 si no.

El error del árbol de regresión en la iteración bth se utiliza para calcular la constante ?b. Esta constante se utiliza para actualizar el peso (wb (i). En AdaBoost.M1 (Freund), la constante se calcula como

ab= ln((1-eb)/eb)

En AdaBoost.M1 (Breiman), la constante se calcula como

ab= 1/2ln((1-eb)/eb)

En SAMME, la constante se calcula como

ab= 1/2ln((1-eb)/eb + ln(k-1) donde k es el número de clases

donde, el número de categorías es igual a 2, SAMME se comporta de la misma como AdaBoost Breiman.

En cualquiera de las tres implementaciones (Freund, Breiman o SAMME), el nuevo peso para la iteración (b + 1)será

Después, todos los pesos se reajustan a la suma de 1. Como resultado, se aumentan las ponderaciones asignadas a las observaciones a las que se asignaron valores predichos inexactos y se disminuyen las ponderaciones asignadas a las observaciones a las que se asignaron valores predichos precisos. Este ajuste obliga al siguiente modelo de regresión a poner más énfasis en los registros a los que se asignaron predicciones inexactas. (¿Esto ? la constante también se usa en el cálculo final, lo que le dará al modelo de regresión con el error más bajo más influencia.) Este proceso se repite hasta que b = Número de alumnos débiles. A continuación, el algoritmo calcula el promedio ponderado entre todos los alumnos débiles y asigna ese valor al registro. El impulso generalmente produce mejores modelos que el ensacado; sin embargo, tiene una desventaja, ya que no es paralelizable. Como resultado, si el número de estudiantes débiles es grande, el impulso no sería adecuado.

El método de árboles aleatorios (bosques aleatorios) es una variación del ensacado. Este método funciona entrenando múltiples árboles de regresión débiles utilizando un número fijo de entidades seleccionadas aleatoriamente (sqrt para la clasificación y número de entidades/3 para la predicción), luego toma el valor promedio para los estudiantes débiles y asigna ese valor al predictor fuerte. Por lo general, el número de árboles débiles generados podría variar de varios cientos a varios miles, dependiendo del tamaño y la dificultad del conjunto de entrenamiento. Los árboles aleatorios son paralelizables, ya que son una variante de ensacado. Sin embargo, dado que tandom trees selecciona una cantidad limitada de características en cada iteración, el rendimiento de los árboles aleatorios es más rápido que el embolsado.

Los métodos de conjuntos de árboles de regresión son métodos muy poderosos, y típicamente dan como resultado un mejor rendimiento que un solo árbol. Esta adición de características en XLMiner V2015 proporciona modelos de predicción más precisos, y debe considerarse sobre el método de árbol único.