8.2: Aaltofunktiot
vetyatomin Schrödingerin yhtälön ratkaisut ovat funktioita, jotka ovat pallomaisen harmonisen funktion ja säteittäisen funktion tuotteita.
\
vetyatomin aaltoluvut riippuvat kolmesta muuttujasta r, \(\theta\) ja \(\varphi \) sekä kolmesta kvanttiluvusta n, \(l\) ja \(m_l\). Muuttujat antavat elektronin sijainnin suhteessa protoniin pallokoordinaateissa. Aaltofunktion \(| \psi (r, \theta, \varphi )|^2\) absoluuttinen neliö, jota arvioidaan pisteissä \(r\), \(\theta\) ja \(\varphi\), antaa todennäköisyystiheyden elektronin löytymiselle differentiaalitilavuuden \(d \tau\) sisällä, jonka keskipisteenä on R, \(\theta\) ja \(\varphi\).
harjoitus \(\PageIndex{1}\)
mikä on integraalin arvo
\
kvanttiluvuilla on nimet: \(n\) kutsutaan pääkvanttiluvuksi, \(l\) kulmamomenttikvanttiluvuksi ja \(m_l\) magneettiseksi kvanttiluvuksi, koska (kuten kohdassa 8.4 nähdään) magneettikentän energia riippuu \(m_l\). Usein \(l\) kutsutaan atsimutaalikvanttiluvuksi, koska se on seurausta \(\theta\)-yhtälöstä, johon liittyy atsimutaalikulma \(\Theta\) viitaten kulmaan zeniitissä.
näillä kvanttiluvuilla on erityisiä arvoja, jotka määräytyvät Schrödingerin yhtälölle asetettujen fysikaalisten rajoitteiden tai reunaehtojen mukaan: \(n\) on oltava kokonaisluku suurempi kuin 0, \(l\) voi olla arvot 0‑n-1, ja \(m_l\) voi olla \(2L + 1\) arvot vaihtelevat \(‑l\) – \(+l\) yksikkö-tai kokonaislukuasteilla. Kvanttiluvun \(l\) arvot koodataan yleensä kirjaimella: s tarkoittaa 0, p tarkoittaa 1, d tarkoittaa 2, f tarkoittaa 3; seuraavat koodit jatkuvat aakkosjärjestyksessä(esim. g tarkoittaa \(l = 4\)). Kvanttiluvut määrittelevät fysikaalisten suureiden kvantisoinnin. Vetyatomin eri tilojen diskreetit energiat ilmoitetaan \(n\), kulmamomentin suuruus \(l\), ja yksi kulmamomentin komponentti(kemistit valitsevat yleensä Z‑komponentiksi) saadaan \(m_l\). Niiden orbitaalien kokonaismäärä, joiden arvo on \(n\), on \(n^2\).
Exercise \(\PageIndex{2}\)
harkitse useita arvoja n: lle ja osoita, että orbitaalien lukumäärä kutakin n: ää kohti on \(n^2\).
harjoitus \(\PageIndex{3}\)
muodosta taulukko, jossa on yhteenveto kvanttilukujen n, \(l\) ja \(m_l\) sallituista arvoista. vedyn energiatasoille 1-7.
harjoitus \(\PageIndex{4}\)
notaatio 3D määrittää vetyatomin elektronin kvanttiluvut. Mitkä ovat arvot n ja \(l\)? Mitkä ovat energian ja kulmamomentin arvot? Mitkä ovat magneettisen kvanttiluvun mahdolliset arvot? Mitkä ovat mahdolliset suuntaukset kulmamomenttivektorille?
vetyatomin aaltofunktioita, \(\psi (r, \theta , \varphi )\), kutsutaan atomiorbitaaleiksi. Atomiorbitaali on funktio, joka kuvaa yhtä elektronia atomissa. Aaltofunktiota, jossa N = 1, \(l=1\) ja \(m_l\) = 0 kutsutaan 1s-orbitaaliksi, ja tämän funktion kuvaaman elektronin sanotaan olevan ”in” LS-orbitaalilla, eli sillä on 1s-orbitaali. Rajoitteet \(n\), \(l)\), ja \(m_l\), jotka on asetettu ratkaisun aikana vetyatomin Schrödingerin yhtälö selittää, miksi on olemassa yksi 1s orbitaali, miksi on kolme 2p orbitaalit, viisi 3d orbitaalit, jne. Kun tarkastelemme luvun 9 monielektroniatomeja, huomaamme, että nämä rajoitteet selittävät jaksollisen järjestelmän ominaisuudet. Toisin sanoen Jaksollinen järjestelmä on ilmentymä Schrödingerin mallista ja fysikaalisista rajoitteista, jotka on asetettu Schrödingerin yhtälön ratkaisujen saamiseksi vetyatomille.
elektronisen aaltofunktion vaihtelun visualisointi \(r\), \(\theta\) ja \(\varphi\) on tärkeää, koska aaltofunktion absoluuttinen neliö kuvaa atomin tai molekyylin varausjakaumaa (elektronitodennäköisyystiheys). Varausjakauma on kemiassa keskeinen, koska se liittyy kemialliseen reaktiivisuuteen. Esimerkiksi yhden molekyylin elektronipuutteinen osa vetää puoleensa toisen molekyylin elektronirikasta aluetta, ja tällaisilla vuorovaikutuksilla on suuri merkitys kemiallisissa vuorovaikutuksissa, jotka vaihtelevat substituutio-ja additioreaktioista proteiinin laskostumiseen ja substraattien vuorovaikutukseen entsyymien kanssa.
aaltofunktioiden ja varausjakaumien visualisointi on haastavaa, koska se vaatii kolmen muuttujan funktion käyttäytymisen tutkimista kolmiulotteisessa avaruudessa. Tätä visualisointia helpottaa se, että tarkastellaan säteittäisiä ja kulmikkaita osia erikseen, mutta säteittäisten ja kulmikkaiden osien piirtäminen erikseen ei paljasta orbitaalin muotoa kovin hyvin. Muoto voidaan paljastaa paremmin todennäköisyystiheysjuonessa. Jos haluat tehdä tällaisen kolmiulotteisen kuvaajan, Jaa tila pieniin tilavuuselementteihin, laske \(\psi^* \psi\) jokaisen tilavuuselementin keskellä ja sitten varjosta, stippaa tai väritä tämä tilavuuselementti suhteessa \(\psi^* \psi\) suuruuteen. Älä sekoita tällaisia tontteja polaarisiin tontteihin, jotka näyttävät samanlaisilta.
Todennäköisyystiheydet voidaan esittää myös ääriviivakarttojen avulla, kuten kuvassa \(\PageIndex{1}\).
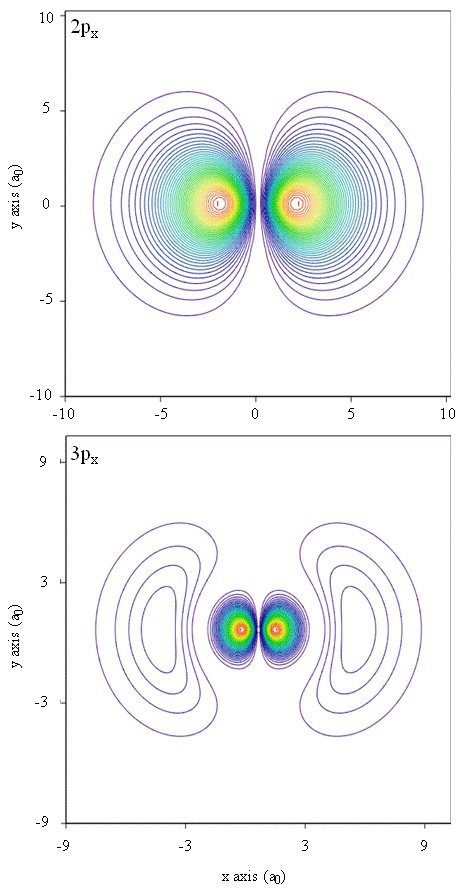
toinen esitystekniikka, virtuaalitodellisuuden mallinnus, pitää elektronitiheyksien esittämistä lupaavana. Kuvittele esimerkiksi, että pystyt kokemaan elektronitiheyden voimana tai vastuksena taikasauvalla, jolla liikut kolmiulotteisessa avaruudessa. Tällaisia haptisiksi kutsuttuja laitteita on jo olemassa ja niitä käytetään tieteellisen tiedon esittämiseen. Eikö samoin olisi kiinnostavaa ”lentää” atomiorbitaalin läpi ja kokea elektronitiheyden muutoksia värimuutoksina tai sameuden muuttumisina? Parhaillaan kehitetään erityisesti suunniteltuja huoneita, joissa on 3D-näytöt ja ”älykkäät” lasit, jotka antavat palautetta katsojan katseen suunnasta, jotta voimme kokea tällaisia tuntemuksia.
menetelmät atomiorbitaalien säteittäisten osien erilliseksi tutkimiseksi antavat hyödyllistä tietoa varaustiheyden jakautumisesta orbitaalien sisällä. Radiaalifunktioiden \(r(r)\) kaaviot kuviossa \(\PageIndex{2}\) piirretyille 1s -, 2s-ja 2p-orbitaaleille.
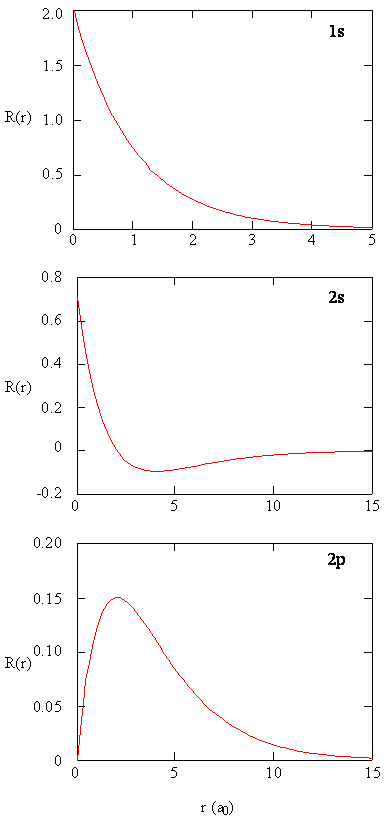
Kuvan \(\PageIndex{2}\) 1s-funktio alkaa suurella positiivisella arvolla tumassa ja hajoaa eksponentiaalisesti olemattomaksi 5 Bohr-säteen jälkeen. Suuri arvo ytimessä voi olla yllättävää, mutta kuten tulemme myöhemmin näkemään, todennäköisyys löytää elektroni ydin on häviävän pieni.
huomaa seuraavaksi, miten 2S-orbitaalin säteisfunktio, luku \(\PageIndex{2}\), menee nollaan ja muuttuu negatiiviseksi. Tämä käyttäytyminen paljastaa, että funktiossa on säteittäinen solmu. Säteittäissolmu syntyy, kun säteisfunktio on nolla muutoin kuin pisteessä \(r = 0\) tai \(R = ∞\). Atomiorbitaalien solmut ja rajoittava käyttäytyminen ovat molemmat hyödyllisiä tunnistettaessa, mikä orbitaali on kuvattu millä aaltofunktiolla. Esimerkiksi kaikilla s-funktioilla on nollasta poikkeavia aaltofunktioarvoja pisteessä \(r = 0\), mutta p, d, f ja kaikki muut funktiot menevät origossa nollaan. On hyvä muistaa, että aaltofunktiossa on \(n-1-l\) säteittäisiä solmuja, mikä tarkoittaa, että 1s-orbitaalilla ei ole säteittäisiä solmuja, 2s: llä on yksi säteittäinen solmu ja niin edelleen.
harjoitus \(\PageIndex{5}\)
tutkii säteittäisten aaltojen matemaattisia muotoja. Mikä ominaisuus funktioissa saa osan niistä menemään nollaan origossa, kun taas S-funktiot eivät mene nollaan origossa?
harjoitus \(\PageIndex{6}\)
mikä matemaattinen ominaisuus kussakin säteisfunktiossa ohjaa säteittäisten solmujen määrää?
harjoitus \(\PageIndex{7}\)
millä r: n arvolla 2s-säteissolmu esiintyy?
harjoitus \(\PageIndex{8}\)
tee taulukko, josta saadaan energia, säteittäisten solmujen lukumäärä sekä kulmasolmujen lukumäärä ja solmujen kokonaismäärä kullekin funktiolle siten, että N = 1, 2 ja 3. Tunnista suhde energian ja solmujen määrä. Tunnista suhde määrä säteittäisiä solmuja ja määrä kulmasolmuja.
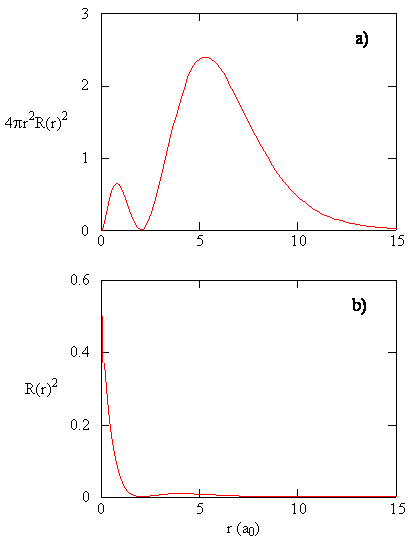
Suure \(R (r) ^* R(r)\) antaa säteittäisen todennäköisyystiheyden eli todennäköisyystiheyden sille, että elektroni on pisteessä, joka sijaitsee etäisyydellä \(r\) protonista. Kolmentyyppisten atomiorbitaalien säteittäiset todennäköisyystiheydet piirretään kuvioon (\PageIndex{3}\).
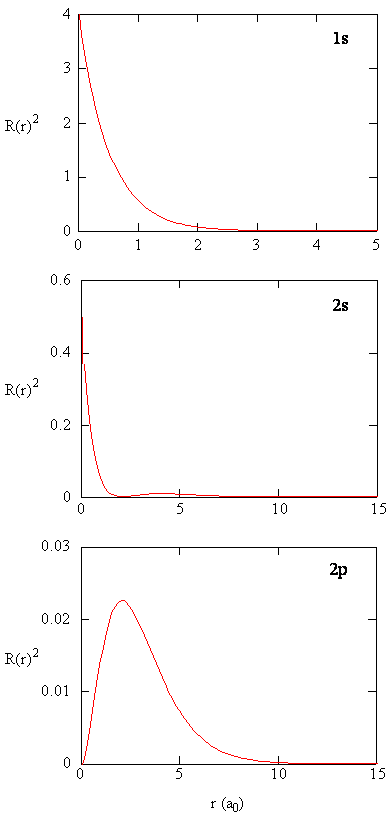
kun jokaisen r: n arvon säteittäinen todennäköisyystiheys kerrotaan kyseisen r: n arvon edustamalla pallopinnan alueella, saadaan säteittäinen jakaumafunktio. Säteittäinen jakaumafunktio antaa todennäköisyystiheyden sille, että elektroni löytyy mistä tahansa sellaisen pallon pinnalta, joka sijaitsee etäisyydellä R protonista. Koska pallopinnan pinta-ala on \(4 \pi r^2\), säteittäisen jakauman funktio on \(4 \pi r^2 R(r) ^* R(r)\).
säteittäiset jakaumafunktiot on esitetty kuvassa \(\PageIndex{4}\). Pienillä R-arvoilla säteittäinen jakaumafunktio on pieni, koska pienten säteiden pieni pinta-ala moduloi säteittäisen todennäköisyystiheysfunktion suurta arvoa ytimen lähellä. Kun lisäämme \(r\), pinta-ala, joka liittyy tiettyyn r: n arvoon, kasvaa, ja \(R^2\) termi aiheuttaa säteittäisen jakaumafunktion kasvamisen, vaikka säteittäisen todennäköisyystiheyden pieneneminen alkaa. Suurilla arvoilla \(r\) säteittäisen funktion eksponentiaalinen hajoaminen on suurempi kuin \(R^2\) termin aiheuttama kasvu ja säteittäinen jakaumafunktio pienenee.
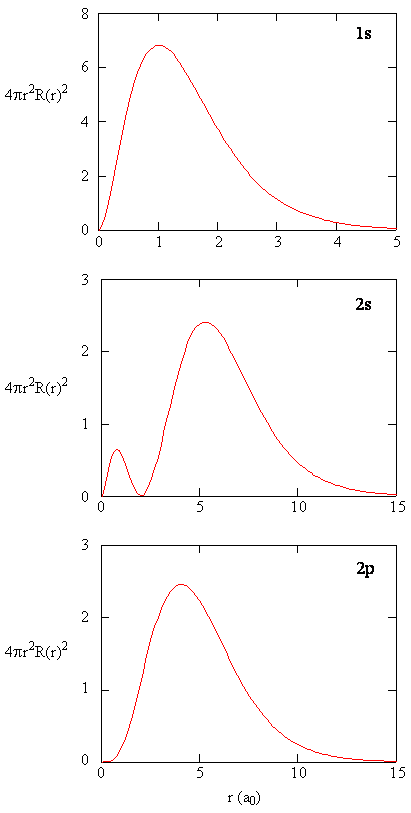
Exercise \(\PageIndex{9}\)
Kirjoita laatuvertailu säteittäisestä funktiosta ja säteittäisestä jakaumafunktiosta 2s-orbitaalille. Katso kuva (\PageIndex{5}\)
avustajat ja attribuutit
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (”atomien ja molekyylien Kvanttitilat”)