Antennit säteilevät sähkömagneettista energiaa tiedon lähettämiseen tai vastaanottamiseen. Siksi termit Energia ja voima liittyvät näihin sähkömagneettisiin aaltoihin, ja meidän on keskusteltava niistä. Sähkömagneettisella Aallolla on sekä sähkö-että magneettikenttiä.

tarkastellaan aaltoa millä tahansa hetkellä, jota voidaan tarkastella molemmilla vektoreilla. Seuraavassa kuvassa esitetään sähkö-ja magneettikentän komponenttien esitys sähkömagneettisessa aallossa.

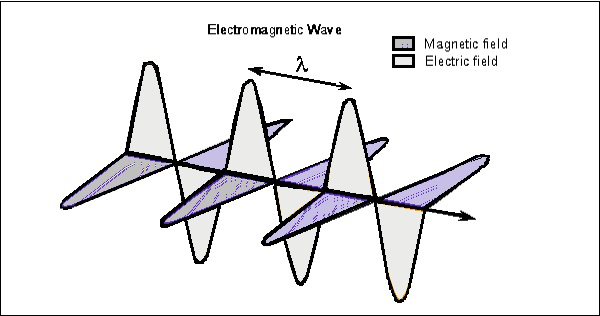
SÄHKÖAALTO esiintyy pystysuorana EM-aallon etenemiselle, kun taas magneettinen Aalto sijaitsee vaakasuorassa. Molemmat kentät ovat suorassa kulmassa toisiinsa nähden.

Poynting-vektori

Poynting-vektori kuvaa em-Aallon energiaa aikayksikköä kohti pinta-alayksikköä kohti tiettynä hetkenä. John Henry Poynting johti tämän vektorin ensimmäisen kerran vuonna 1884, ja siksi se nimettiin hänen mukaansa.

määritelmä − ”Poynting vektori antaa energian siirtonopeuden pinta-alayksikköä kohti”

tai

”energia, jonka aalto kuljettaa aikayksikköä pinta-alayksikköä kohti, saadaan Poynting-vektorista.”

Poynting-vektoria esittää Ŝ.

yksiköt

Poynting-vektorin SI-yksikkö on W / m2.

matemaattinen lauseke

Suure, jota käytetään kuvaamaan sähkömagneettisiin aaltoihin liittyvää voimaa, on hetkellinen Poynting-vektori, joka määritellään seuraavasti:

$$\hat{s} = \hat{E} \times \hat{h}$$

missä

• $\hat{s}$ on hetkellinen Poynting-vektori (W / m2).

$\hat{E}$ on hetkellinen Sähkökentän voimakkuus (V / m).

$\hat{h}$ on hetkellinen magneettikentän voimakkuus (A / m).

tärkeä tässä huomioitava seikka on se, että E: n magnitudi on suurempi kuin H em-aallossa. Molemmat tuottavat kuitenkin saman verran energiaa. Ŝ on vektori, jolla on sekä suunta että suuruus. Ŝ: n suunta on sama kuin aallon nopeus. Sen suuruus riippuu E: stä ja H: sta.

Poynting-vektorin derivointi

jotta Poynting-vektorista olisi selkeä käsitys, käykäämme läpi tämän Poynting-vektorin derivointi vaiheittaisessa prosessissa.

kuvitellaanpa, että EM-Aalto läpäisee alueen (A), joka on kohtisuorassa x-akseliin nähden, jota pitkin aalto kulkee. Kulkiessaan A: n läpi äärettömän pienessä ajassa (dt) aalto kulkee matkan (dx).

$$dx = C\ DT$$

Where

$$c = velocity\ of\ light = 3\kertaa 10^{8}m/s$$$$tilavuus, dv = Adx = AC\ dt$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ DT)$$$= \epsilon_{0} AC \ E^{2}\ DT p>näin ollen ajassa (DT) siirretyn energian pinta −ala (A) on – $$ s = \frac{energia}{time\times area} = \frac{DW}{DT\ a} = \frac{\epsilon_{0}Ace^{2}\ dt}{dt\ a} = \epsilon_{0}C\:E^{2}$$

koska

$ $ \frac{E}{h} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \ then\ s= \frac{CB^{2}}{\mu_{0}}$$

koska

$$c = \frac{E}{H} \ then \ s = \frac{EB}{\mu_{0}}$$$$= \hat{s} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Ŝ merkitsee Poynting-vektoria.

yllä oleva yhtälö antaa meille energian aikayksikköä kohti, pinta-alayksikköä kohti minä tahansa ajan hetkenä, jota kutsutaan Poynting-vektoriksi.