Kalman suodattimet

tietojen yhdistämiseen käytettävää algoritmia kutsutaan Kalman-suodattimeksi.

Kalman-suodatin on yksi suosituimmista algoritmeista datafuusiossa. Rudolph Kalman keksi sen vuonna 1960, ja sitä käytetään nykyään puhelimissamme tai satelliiteissamme navigointiin ja seurantaan. Tunnetuin suodattimen käyttö oli Apollo 11: n lennon aikana, jolloin miehistö lähetettiin ja tuotiin takaisin kuuhun.

milloin Kalman-suodatinta käytetään ?

tiedon fuusiossa voidaan käyttää Kalman-suodatinta, jolla voidaan arvioida dynaamisen järjestelmän (kehittyy ajan mukana) tilaa nykyhetkessä (suodatus), menneisyydessä (tasoitus) tai tulevaisuudessa (ennustaminen). Autonomisiin ajoneuvoihin upotetut sensorit lähettävät toimenpiteitä, jotka ovat joskus puutteellisia ja meluisia. Antureiden epätarkkuus (melu) on erittäin tärkeä ongelma ja se voidaan hoitaa Kalman-suodattimilla.

systeemin tilan estimointiin käytetään Kalman-suodatinta, jota merkitään X. Tämä vektori koostuu asemasta p ja nopeudesta v.

jokaiseen estimaattiin liitetään epävarmuuden mitta P.

suorittamalla antureiden fuusio otamme huomioon eri tiedot samasta kohteesta. Tutka voi arvioida jalankulkijan olevan 10 metrin päässä, kun taas Lidar arvioi sen olevan 12 metriä. Kalman-suodattimien käyttö antaa tarkan käsityksen siitä, kuinka monta metriä jalankulkija todella on, poistamalla kahden anturin melun.

Kalman-suodatin voi tuottaa arvioita ympärillään olevien kappaleiden tilasta. Arvioon tarvitaan vain nykyiset havainnot ja aiempi ennuste. Mittaushistoriaa ei tarvita. Tämä työkalu on siis kevyt ja paranee ajan myötä.

miltä se näyttää

tilaa ja epävarmuutta edustavat Gaussilaiset.

Gaussin on jatkuva funktio, jonka alla pinta-ala on 1. Näin voimme esittää todennäköisyyksiä. Olemme normaalijakauman todennäköisyydellä. Kalman-suodattimien yksimodaalisuus tarkoittaa, että meillä on joka kerta yksi piikki, jonka avulla voimme arvioida järjestelmän tilaa.

meillä on keskiarvo μ, joka edustaa tilaa, ja varianssi σ2, joka edustaa epävarmuutta. Mitä suurempi varianssi, sitä suurempi epävarmuus.

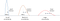
Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Käytämme sensoreidemme havaintoja korjataksemme ennustetun tilan ja saadaksemme tarkemman arvion.

arvioon Kalman-suodatin tarvitsee vain nykyiset havainnot ja aiemman ennusteen. Mittaushistoriaa ei tarvita.

matematiikka

Kalman-suodattimien taustalla oleva matematiikka koostuu matriisien lisäyksistä ja kertolaskuista. Meillä on kaksi vaihetta: ennustaminen ja päivitys.

ennustus
ennusteemme koostuu tilan x’ ja epävarmuuden P’ estimoinnista hetkellä t edellisistä tiloista x ja P ajasta t-1.

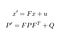
• F: siirtymämatriisi T-1: stä t: iin
• ν: kohina lisätty
• Q: Kovarianssimatriisi mukaan lukien kohina

Update
päivitysvaiheessa käytetään anturin z-mittausta ennusteen korjaamiseksi ja siten ennustamiseksi x ja P.

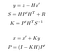
• y: todellisen mittauksen ja ennustuksen ero, eli virhe.
• S: Estimated system error
• H: matrix of transition between the marker of the sensor and ours.
• R: Kovarianssimatriisi, joka liittyy anturimeluun (anturin valmistajan antama).
• K: Kalman voitto. Kerroin 0: n ja 1: n välillä kuvastaa tarvetta korjata ennustettamme.

päivitysvaiheessa on mahdollista arvioida X ja P lähempänä todellisuutta kuin mitä mittaukset antavat.

Kalman-suodatin mahdollistaa ennustamisen reaaliaikaisesti, ilman ennakkotietoja. Käytämme matemaattista mallia, joka perustuu matriisien kertolaskuun kullekin ajalle, jossa määritellään tila x (sijainti, nopeus) ja epävarmuus P.

Représentation Prior/Posterior

Tämä kaavio näyttää, mitä Kalman-suodattimessa tapahtuu.

• ennustettu tila-arvio edustaa ensimmäistä arviotamme, ennustusvaihettamme. Puhumme priorista.
• mittaus on mittaus yhdeltä antureistamme. Meillä on parempi epävarmuus, mutta antureiden melu tekee siitä mittauksen, jota on aina vaikea arvioida. Puhumme todennäköisyydestä.
• optimaalinen tila-arvio on meidän päivitysvaihe. Epävarmuus on tällä kertaa heikointa, keräsimme tietoa ja saimme luoda varmemman arvon kuin pelkällä sensorillamme. Tämä arvo on paras arvauksemme. Puhumme posteriorista.

se, mitä Kalman suodatin toteuttaa, on todellisuudessa Bayesin sääntö.

Kalman-suodattimessa silmukoidaan ennusteita mittauksista. Ennusteemme ovat aina tarkempia, koska pidämme tietyn määrän epävarmuutta ja laskemme säännöllisesti ennusteemme ja todellisuutemme välisen virheen. Pystymme matriisikertoimista ja todennäköisyyskaavoista arvioimaan ympärillämme olevien ajoneuvojen nopeuksia ja asemia.

”Extended/Unscented” suodattimet ja epälineaarisuus

syntyy olennainen ongelma. Kaikki matemaattiset kaavamme toteutetaan lineaarisilla funktioilla, joiden tyyppi on y = ax + b.
Kalman-suodatin toimii aina lineaaristen funktioiden kanssa. Toisaalta, kun käytämme tutkaa, data ei ole lineaarista.

tutka näkee maailman kolmella mittarilla:

nämä kolme arvoa tekevät mittauksestamme epälineaarisen, koska mukaan otetaan kulma φ.

tavoitteenamme on muuntaa data ρ, φ, ρ Karteesiseksi dataksi (px, py, vx, vy).

Jos syötämme epälineaarista dataa Kalman-suodattimeen, tuloksemme ei ole enää uni-modaalisessa Gaussin muodossa, emmekä voi enää arvioida sijaintia ja nopeutta.

joten käytämme approksimaatioita, minkä vuoksi työstämme kahta menetelmää:
-laajennetut Kalman – suodattimet käyttävät mallin linearisointiin jacobian-ja taylorinsarjoja.
– Unscented Kalman-suodattimet käyttävät tarkempaa approksimaatiota mallin linearisointiin.

on olemassa tekniikoita, joiden avulla suodattimemme voivat arvioida niiden kohteiden sijainnin ja nopeuden, joita haluamme seurata.