Blog
edellisessä blogikirjoituksessa keskustelimme siitä, miten supermarketit käyttävät tietoja ymmärtääkseen paremmin kuluttajien tarpeita ja viime kädessä kasvattaakseen kokonaiskulutustaan. Yksi suurten vähittäiskauppiaiden käyttämistä keskeisistä tekniikoista on Market Basket Analysis (MBA), jossa selvitetään tuotteiden välisiä assosiaatioita etsimällä tuotteiden yhdistelmiä, jotka usein esiintyvät samanaikaisesti liiketoimissa. Toisin sanoen sen avulla supermarketit voivat tunnistaa ihmisten ostamien tuotteiden väliset suhteet. Esimerkiksi kynää ja paperia ostavat asiakkaat ostavat todennäköisesti kumin tai viivoittimen.
”Markkinakorianalyysin avulla vähittäiskauppiaat voivat tunnistaa ihmisten ostamien tuotteiden väliset suhteet.”
vähittäiskauppiaat voivat käyttää MBA: sta saatuja oivalluksia monin tavoin, mukaan lukien:
- ryhmittelemällä tuotteita, jotka esiintyvät yhdessä kaupan ulkoasun suunnittelussa ristiinmyynnin mahdollisuuden lisäämiseksi;
- ajaa online-suositusmoottoreita (”asiakkaat, jotka ostivat tämän tuotteen, katsoivat myös tätä tuotetta”); ja
- kohdentamalla markkinointikampanjoita lähettämällä asiakkaille tarjouskuponkeja, jotka koskevat heidän äskettäin ostamiinsa tuotteisiin liittyviä tuotteita.
ottaen huomioon, kuinka suosittu ja arvokas MBA on, ajattelimme laatia seuraavan vaiheittaisen oppaan, jossa kuvaillaan, miten se toimii ja miten voit tehdä oman Markkinakorianalyysin.
miten Markkinakorianalyysi toimii?
MBA: n suorittamiseen tarvitaan ensin tietokokonaisuus transaktioista. Kukin tapahtuma edustaa ryhmää kohteita tai tuotteita, jotka on ostettu yhdessä ja usein kutsutaan ”itemset”. Esimerkiksi yksi itemsetti voi olla: {lyijykynä, paperi, niitit, kumi}, jolloin kaikki nämä tuotteet on ostettu yhdellä kaupalla.
MATERIAALITASEALUEELLA taloustoimet analysoidaan yhdistymissääntöjen määrittämiseksi. Yksi sääntö voisi olla esimerkiksi: {pencil, paper} => {rubber}. Tämä tarkoittaa sitä, että jos asiakkaalla on kauppa, jossa on kynä ja paperia, niin he ovat todennäköisesti kiinnostuneita ostamaan myös kumin.
ennen kuin kauppias toimii säännön mukaan, hänen on tiedettävä, onko riittävästi näyttöä siitä, että se johtaa hyödylliseen lopputulokseen. Mittaamme siis säännön vahvuutta laskemalla seuraavat kolme mittaria (huomaa, että muita mittareita on saatavilla, mutta nämä ovat kolme yleisimmin käytettyä):
tuki: niiden tapahtumien prosenttiosuus, jotka sisältävät kaikki itemsetin erät (esim.lyijykynä, paperi ja kumi). Mitä korkeampi tuki, sitä useammin itemset esiintyvät. Sääntöjä, joilla on suuri tuki, pidetään parempina, koska niitä voidaan todennäköisesti soveltaa moniin tuleviin liiketoimiin.
luottamus: todennäköisyys sille, että liiketoimi, joka sisältää säännön vasemmalla puolella olevat kohteet (esimerkissämme kynä ja paperi), sisältää myös oikeanpuoleisen esineen (kumi). Mitä suurempi luottamus, sitä suurempi todennäköisyys, että kohde oikealla puolella on ostettu tai, toisin sanoen, suurempi tuotto korko voit odottaa tietyn säännön.
Hissi: todennäköisyys kaikkien erien sääntö esiintyy yhdessä (tunnetaan myös nimellä tuki) jaettuna tuotteen todennäköisyydet kohteita vasemmalla ja oikealla puolella esiintyy ikään kuin ei olisi yhteyttä niiden välillä. Jos esimerkiksi lyijykynä, paperi ja kumi esiintyisivät yhdessä 2,5 prosentissa kaikista liiketoimista, lyijykynä ja paperi 10 prosentissa liiketoimista ja kumi 8 prosentissa liiketoimista, hissi olisi: 0.025/(0.1*0.08) = 3.125. Yli 1: n nosto viittaa siihen, että kynän ja paperin läsnäolo lisää todennäköisyyttä, että kaupassa esiintyy myös kumia. Yleisesti ottaen lift tiivistää säännön vasemmalla ja oikealla puolella olevien tuotteiden välisen yhteyden lujuuden; mitä suurempi hissi, sitä suurempi on näiden kahden tuotteen välinen yhteys.
Markkinakorianalyysin suorittamiseksi ja mahdollisten sääntöjen tunnistamiseksi käytetään yleisesti ”Apriori-algoritmiksi” kutsuttua tiedonlouhinta-algoritmia, joka toimii kahdessa vaiheessa:
- tunnistaa järjestelmällisesti tietojoukossa usein esiintyvät tietoryhmät, joiden tuki ylittää ennalta määritetyn kynnysarvon.
- laskee kaikkien mahdollisten sääntöjen varmuuden ottaen huomioon toistuvat erittelyt ja pitää vain ne, joiden luottamus ylittää ennalta määrätyn kynnysarvon.
kynnysarvot tuen ja luottamuksen asettamiseksi ovat käyttäjän määrittämiä ja ne todennäköisesti vaihtelevat tapahtumatietoaineistojen välillä. R: llä on oletusarvot, mutta suosittelemme, että kokeilet näitä nähdäksesi, miten ne vaikuttavat palautettujen sääntöjen määrään (lisää tästä alla). Lopuksi, vaikka Apriori-algoritmi ei käytä liftiä sääntöjen laatimiseen, näet seuraavasta, että käytämme liftiä tutkiessamme sääntöjä, jotka algoritmi palauttaa.
Markkinakorianalyysin suorittaminen R
osoittaaksemme, miten MBA suoritetaan, olemme päättäneet käyttää R: ää ja erityisesti arules-pakettia. Niille, jotka ovat kiinnostuneita olemme sisällyttäneet R-koodi, jota käytimme lopussa tämän blogin.
tässä seuraamme samaa arulesvizin Vinjetissä käytettyä esimerkkiä ja käytämme päivittäistavaramyynnin tietokokonaisuutta, joka sisältää 9 835 yksittäistä kauppaa 169 kappaleella. Ensimmäinen asia, jonka teemme, on tarkastella liiketoimien kohteita ja erityisesti piirtää kuvan 1 25 yleisimmän kohteen suhteellinen esiintymistiheys. Tämä vastaa näiden erien tukea, jos kukin erä sisältää vain yhden erän. Tämä baari tontti kuvaa päivittäistavaroita, joita usein ostetaan tässä kaupassa, ja on huomattava, että tuki jopa yleisin kohteita on suhteellisen alhainen (esimerkiksi yleisin erä esiintyy vain noin 2,5% liiketoimista). Käytämme näitä oivalluksia ilmoittaaksemme vähimmäisrajan ajettaessa Apriori-algoritmia; tiedämme esimerkiksi, että jotta algoritmi voi palauttaa kohtuullisen määrän sääntöjä, meidän on asetettava tukikynnys selvästi alle 0,025: n.
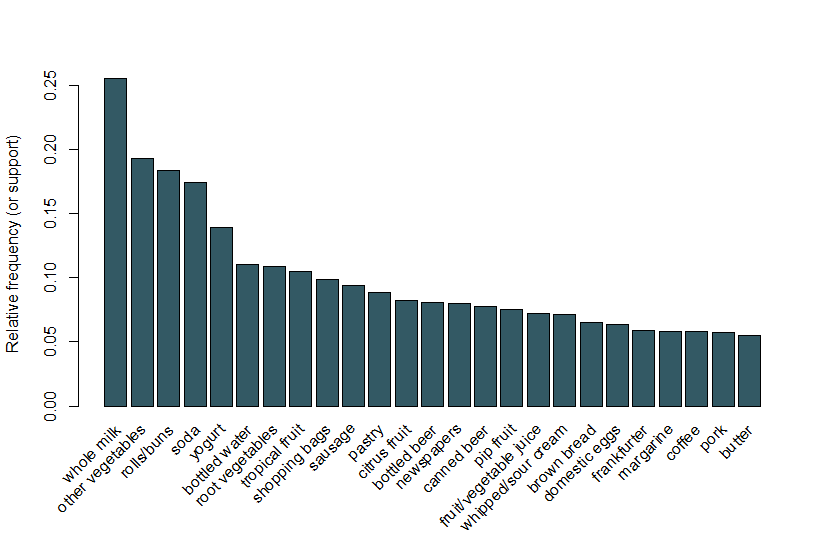
kuva 1 a bar plot of the support of the 25 Most Frequently subject.
asettamalla kannattajakynnykseksi 0,001 ja luottamuskynnykseksi 0,5 voimme suorittaa Apriori-algoritmin ja saada joukon 5,668 tulosta. Nämä raja-arvot on valittu niin, että palautettujen sääntöjen määrä on suuri, mutta määrä vähenisi, jos nostaisimme jompaakumpaa kynnystä. Suosittelemme kokeilemaan näitä raja-arvoja sopivimpien arvojen saamiseksi. Vaikka sääntöjä on liian monta, jotta niitä kaikkia voisi katsoa yksitellen,voidaan katsoa viittä sääntöä, joilla on suurin hissi:
| sääntö | tuki | luottamus | Lift | {instant food products, Soda}=>{jauheliha} | 0, 001 | 0, 632 | 19, 00 | {soda, popcorn}=>{suolaiset välipalat} | 0, 001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. Esimerkiksi ensimmäinen sääntö voisi edustaa sellaista tavaraa, joka on ostettu BBQ: ta varten, toinen elokuvailtaa varten ja kolmas leipomista varten.
sen sijaan, että raja-arvoja käytettäisiin sääntöjen pienentämiseen pienempään sarjaan, on tavallista, että suurempi sääntökokonaisuus palautetaan, jotta on suurempi mahdollisuus laatia asiaa koskevia sääntöjä. Vaihtoehtoisesti voimme käyttää visualisointitekniikoita tarkastaaksemme palautetut säännöt ja tunnistaaksemme ne, jotka ovat todennäköisesti hyödyllisiä.
arulesviz-pakettia käyttäen piirrämme säännöt luottamusta, tukea ja nostetta käyttäen kuvioon 2. Tämä juoni havainnollistaa eri mittareiden välistä suhdetta. On osoitettu, että optimaaliset säännöt ovat ne, jotka ovat niin sanotulla ”tuki-luottamus-rajalla”. Pohjimmiltaan nämä ovat sääntöjä, jotka sijaitsevat tontin oikealla rajalla, jossa joko tuki, luottamus tai molemmat on maksimoitu. Arulesviz-paketin juonifunktiolla on hyödyllinen interaktiivinen funktio, jonka avulla voit valita yksittäisiä sääntöjä (klikkaamalla niihin liittyvää datapistettä), mikä tarkoittaa, että säännöt rajalla voidaan helposti tunnistaa.
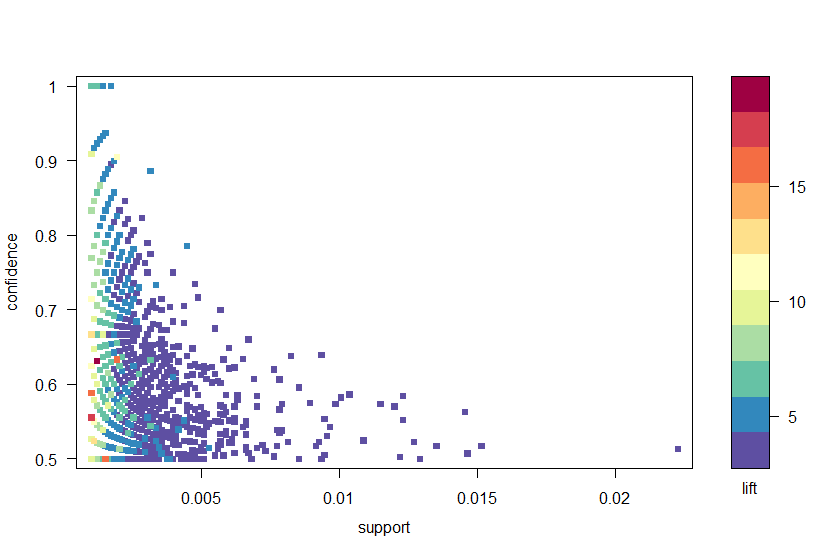
kuva 2: luottamus -, tuki-ja nostomittareiden hajontakaavio.
on olemassa paljon muitakin tontteja, joiden avulla sääntöjä voidaan visualisoida, mutta yksi luku, jota suosittelemme tutkimaan, on kymmenen suurimman säännön kuviopohjainen visualisointi (KS.kuva 3) hissin suhteen (voit sisällyttää enemmän kuin kymmenen, mutta tämäntyyppiset kaaviot voivat helposti sekoittua). Tässä kaaviossa ympyrän ympärille ryhmitellyt kohteet edustavat itemsarjaa ja nuolet osoittavat sääntöjen suhteen. Yksi sääntö on esimerkiksi se, että sokerin ostaminen liittyy jauhojen ja leivinjauheen ostamiseen. Ympyrän koko kuvaa sääntöön liittyvää luottamustasoa ja väri nostotasoa (mitä suurempi ympyrä ja mitä tummempi harmaa, sen parempi).
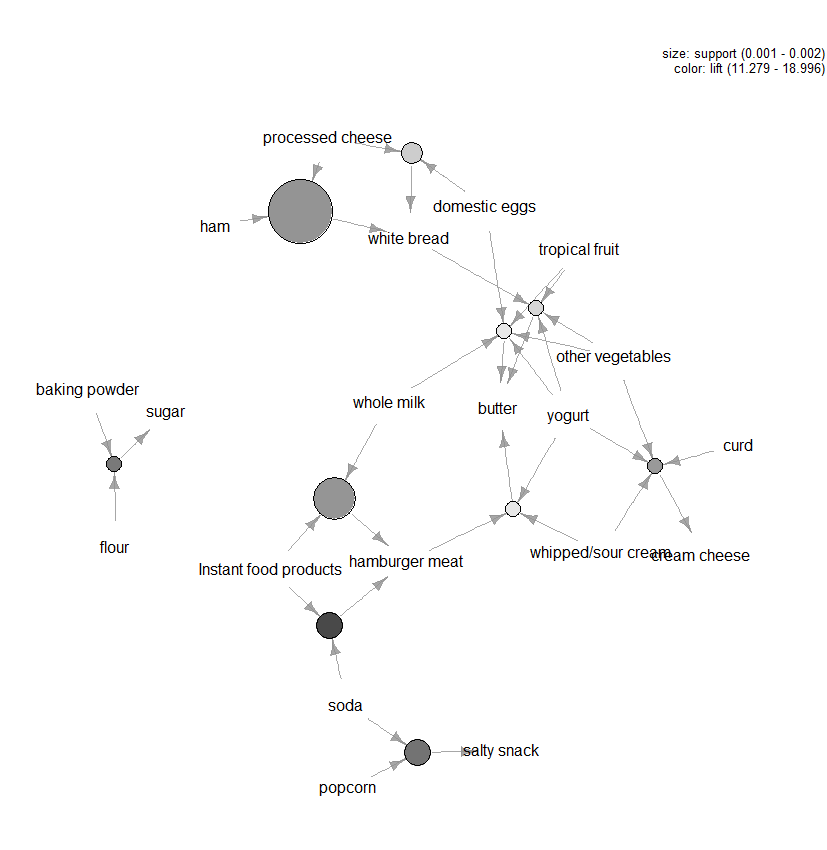
kuva 3: kymmenen ylimmän säännön visualisointi nostovoiman suhteen.
Markkinakorianalyysi on hyödyllinen työkalu kauppiaille, jotka haluavat ymmärtää paremmin ihmisten ostamien tuotteiden välisiä suhteita. On olemassa monia työkaluja, joita voidaan soveltaa suoritettaessa MBA ja hankalimpia näkökohtia analyysi on asettaa luottamusta ja tukea kynnysarvot Apriori algoritmi ja tunnistaa, mitkä säännöt ovat syytä jatkaa. Tyypillisesti jälkimmäinen tehdään mittaamalla sääntöjä niiden kiinnostavuudesta kertovilla mittareilla, käyttäen visualisointitekniikoita ja myös muodollisempia monimuuttujatilastoja. Viime kädessä avain MBA on poimia arvo transaktiotiedot rakentamalla ymmärrystä kuluttajien tarpeisiin. Tällaiset tiedot ovat korvaamattomia, jos olet kiinnostunut markkinointitoimista, kuten ristiinmyynnistä tai kohdennetuista kampanjoista.
Jos haluat tietää lisää siitä, miten voit analysoida tapahtumatietojasi, ota meihin yhteyttä ja autamme mielellämme.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.