31.toukokuuta 1832 Ranskalainen tasavaltalainen vallankumouksellinen Évariste Galois kuoli laukaukseen. Hän oli 20-vuotias. Edellisenä iltana, peläten omaa kuolemaansa, Galois oli kirjoittanut monia kirjeitä, kiihkeästi scribbling ”minulla ei ole aikaa; minulla ei ole aikaa”. Yksi kirjain on erityisen arvokas historiallisista syistä. Kirjeessä Galois väittää itse asiassa käynnistäneensä vallankumouksen. Ei poliittinen. Mutta matemaattinen sellainen.

Galois ’ n aloittama vallankumous osoittautui suuremmaksi ja syvällisemmäksi kuin hän olisi voinut kuvitella! Galois’ n visio on vaikuttanut suuresti matematiikan maisemaan, sillä sen jälkeläiset ovat nousseet ja ottaneet matemaattisen maailman haltuunsa. Tämä jälkeläinen on nyt kaikkialla läsnä ja hallitsee rajatonta maata. Se kulkee nimellä puhdas algebra.

romantisoidakseni edes hieman enemmän Galois’ n dramaattisen elämän tarinaa, tässä tiivistelmä algebrasta tekemästäni dokumentista:

hän ehdottomasti on! Hänen matemaattinen vallankumouksensa ei kuitenkaan sujunut ongelmitta. Kuten muillakin vallankumousjohtajilla, hänellä oli aluksi mitä suurimmat vaikeudet. En kuvitellakseni vallankumousta. Mutta vakuuttaa muut liittymään hänen peli-muuttuva lähestymistapa matematiikkaan. Kun Galois oli vielä elossa, hänen vallankumouksellinen ideoita sai hylättiin useita kertoja, jonka Ranskan tiedeakatemia … koska paras Ranska matemaatikot, että aika kuten Siméon Denis Poisson vain voinut saada sitä! Osittain siksi, että Galois ’lukukelvoton käsiala näkyy oikealla …

vuonna 1843, 10 vuotta Galois’ n kuoleman jälkeen, nerokas ranskalainen matemaatikko Joseph Liouville onnistui lopulta käsittämään joitakin Galois’ n ajatuksia. Kun 3 vuotta työtä, Liouville julkaisi artikkelin selittää niitä. Mutta Liouville artikkeli oli vielä liian kaukaa haettu muiden matemaatikot nauttia ja ymmärtää. Kesti vielä 24 vuotta löytää ranskalainen matemaatikko jäljellä tarpeeksi paremmin ymmärtää Galois ja tehdä hänen ajatuksiaan ontuva. Tämä erinomainen matemaatikko on Camille Jordania. Jordanin vuonna 1870 julkaisema kirja Galois ’ n teoriasta oli niin hyvin kirjoitettu, että saksalainen matemaatikko Felix Klein piti sitä yhtä luettavana kuin saksalaista kirjaa!

se oli ehdottomasti valtava piristysruiske. Mutta se veisi vielä 82 vuotta, että suuri itävaltalainen matemaatikko Emil Artin vihdoin antaa Galois teoria sen moderni muoto, vuonna 1942. Artin ansaitsee paljon kiitosta. Vaikka Galois oli visionary jotka ennakoida tämän vallankumouksen, Artin, monissa aisteissa, on yksi, jotka todella sitoutui vallankumouksen ja kumottiin matematiikka. Kiitos Artin, ja muutama muu, tänään, Galois teoria on tullut väistämätön kulmakivi tutkimuksen matematiikan, runsaasti yllättäviä ja uskomattomia saavutuksia (kuten Wiles ”todiste Fermat’ n suuri lause), sekä valtava säiliö avoimia kysymyksiä ja mysteereitä!

kentät puhtaassa algebrassa

Galois ’ n teoria käsittelee lukujen symmetrioita. Mutta ennen kuin pääsen sinne, minun täytyy esitellä, että saan sinut aseistettua kertomalla sinulle salaisuuden numeroista. Olet varmasti kuullut siitä! Lukiossa sinua luultavasti opetettiin olemaan jättämättä juuria nimittäjiin.

tarkoitan, että $1 / (\sqrt{2}-1)$ ei ollut oikea vastaus. Voitteko auttaa pääsemään eroon neliöjuuri 2 nimittäjä?

Hehe … meitä opetettiin moninkertaistamaan ylös ja alas, jonka konjugaatti, nimittäjä. Tämä konjugaatti saadaan korvaamalla $ – $ nimittäjässä $ + $ (tai päinvastoin):

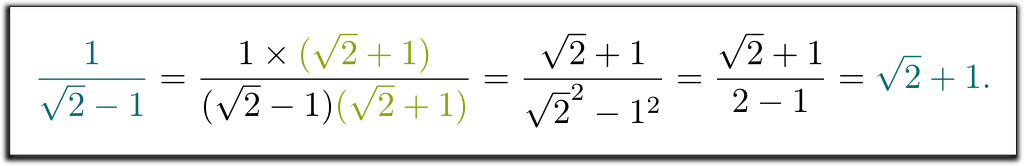
tiedän! Monimutkainen lauseke $1 / (\sqrt{2}-1)$ edustaa samaa lukua kuin $\sqrt{2}+1$. Ja tämä selittää sen, miksi opettajamme halusivat meidän kirjoittavan tulokset tavalla eikä toisella: kun kaikki on kirjoitettu samalla tavalla, kokeet on paljon helpompi korjata!

mutta entä $1 / (\sqrt{2}-1)$? Pääsetkö eroon nimittäjän juuresta? Voiko sitä edes tehdä?

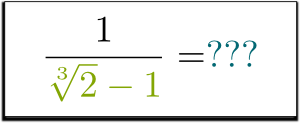
tiedän!

kerro minulle!

Any luck?

Hehe… mielenkiintoista on, että mikä tahansa potenssi $\sqrt{2}-1$ voidaan kirjoittaa potenssien summana $\sqrt{2}$. Itse asiassa sinun tarvitsee vain jakaa tuotteet:

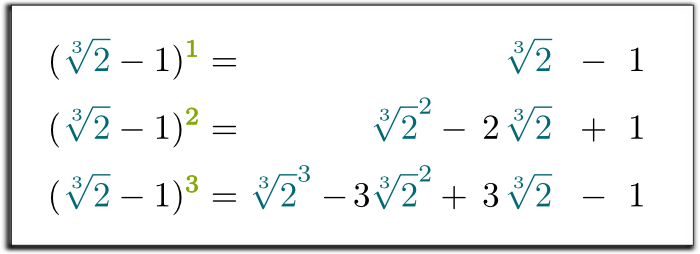
kyllä se on! Tekemällä tämän korvaamisen kolmannessa yhtälössä, olemme osoittaneet, että kolme ensimmäistä potenssia $\sqrt{2}-1$ voidaan kirjoittaa summa Rationaaliluku, $\sqrt{2}$ ja $\sqrt{2}^2$!

joten meillä on nyt 3 yhtälöä, joissa on 2 juurilauseketta haluamme päästä eroon! Näin voimme yhdistää yhtälöt poistaa kaikki root lausekkeet oikealla!

kerrotaan 2 ensimmäistä riviä 3: lla ja lasketaan yhteen kaikki 3 yhtälöä:

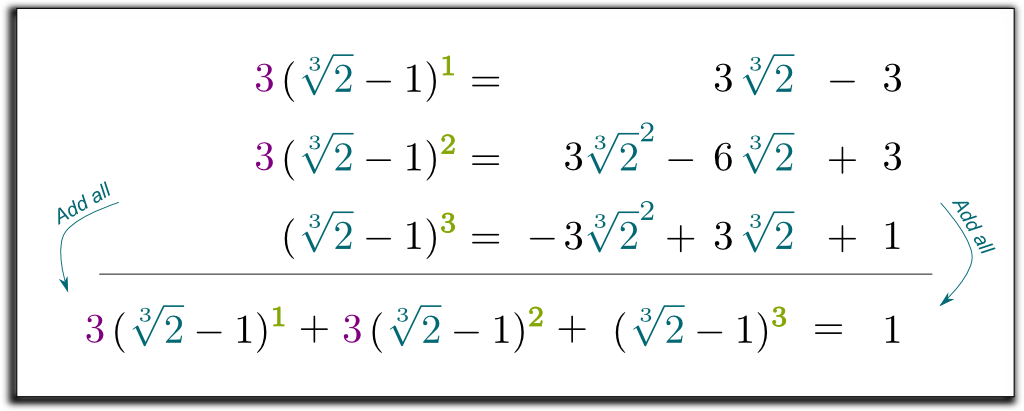
Hehe… siistiä on, että saamamme vasen termi voidaan nyt factorized by $\sqrt{2}-1$! Anna minun ohittaa joitakin tylsiä laskelmia… ja päästä tulokseen $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Joten, päästä eroon juuret nimittäjä, voimme kertoa ylös ja alas $\sqrt{2}^2 + \sqrt{2} + 1$! Lopuksi saadaan seuraava yllättävä ja kaunis kaava:

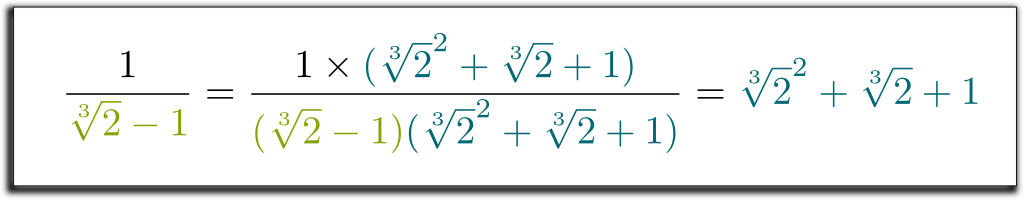
tiedän! Mutta vielä siistimpää on se, että käyttämämme menetelmä on hyvin yleinen! Samanlaisilla tekniikoilla voimme nyt poistaa kaikki radikaalit nimittäjistä!

nyt Galois ’ ta kiinnosti erityisesti se, että menetelmä mahdollisti radikaalien poistamisen nimittäjistä. Vaan, että mikä tahansa määrä radikaaleja nimittäjät vastasi useita radikaaleja päälle. Tämä tarkoitti, että numerot radikaalit päällä olivat stabiileja jako.

on tavallista merkitä $\mathbb Q{2}]$ lukujoukkoa, joka voidaan kirjoittaa potenssien summana $\sqrt{2}$. Koska $\sqrt{2}^3 = 2$ on Rationaaliluku, mikä tahansa potenssien summa $\sqrt{2}$ voidaan itse asiassa kirjoittaa vakiomuodossa $a\sqrt{2}^2 + b\sqrt{2} + c$. Nyt, jos lisäät, vähennät tai kerrot mitkä tahansa kaksi tällaista numeroa, niin ei ole vaikea nähdä, että saamme numeroita, jotka voidaan silti laittaa vakiomuotoon $a\sqrt{2}^2 + b\sqrt{2} + c$. Lisäksi olemme juuri osoittaneet, että kaikkien lukujen käänteisarvo $a\sqrt{2}^2 + b\sqrt{2} + C$ voidaan kirjoittaa myös vakiomuodossa. Tämä osoittaa, että mikä tahansa yhteen -, vähennys -, kerto-ja jakolasku luvuissa $\mathbb Q{2}]$ tuottaa luvun, joka voidaan kirjoittaa vakiomuodossa… ja siten kuuluu $\mathbb Q{2}]$. Puhtaan algebran termein ilmaistuna $\mathbb Q{2}]$ on siis stabiili neljällä klassisella aritmeettisella operaatiolla. Tästä syystä kutsumme sitä pelloksi.

Kenttälaajennusten geometria

kenttä, jonka tunnet parhaiten, on luultavasti rationaalilukujen joukko $\mathbb Q$. Muita esimerkkejä kentistä ovat reaalilukujen joukko $\mathbb R$ ja kompleksilukujen joukko $\mathbb C$. Ja nyt meillä on myös $ \mathbb Q{2}]$. Koska $\mathbb Q{2}]$ on kenttä, joka sisältää kentän $\mathbb Q$, sanomme, että $\mathbb Q{2}] / \mathbb Q$ on kentän laajennus.

se, että $\mathbb Q{2}] / \mathbb Q$ on kentän laajennus, tuottaa hyvin luonnollisen yhteyden kahden kentän välille. Nimittäin $\mathbb Q{2}]$ voidaan nähdä vektoriavaruutena, jossa $\mathbb Q$ on skalaarikenttä. Erityisesti se, että mikä tahansa luku $\mathbb Q{2}]$ voidaan kirjoittaa $\sqrt{2}^2 + b\sqrt{2} + c$ tarkoittaa, että $(1, \sqrt{2}, \sqrt{2}^2)$ muodostaa perustan $\mathbb Q{2}]$: lle $\mathbb Q$-vektoriavaruutena. Ja tämä tarkoittaa, että voimme esittää sen geometrisesti 3-ulottuvuuden avaruutena!

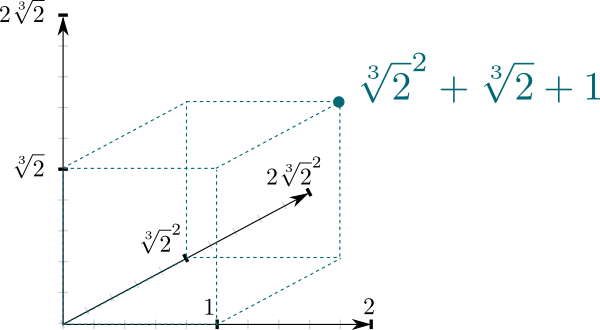
yllä olevan vektoriavaruuden dimensio on kiinnostava kenttälaajennusten ominaisuus. Se tunnetaan aste, ja se on yleisesti merkitty $\big{2}] : \mathbb Q\big] = 3$ esimerkiksi.

Yes! Tähän on itse asiassa melko helppo luoda kenttälaajennus: lisää vain jokin radikaali luku, joka ei kuulu $\mathbb Q{2}]$!

Yes! Tämä loisi kentän $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$. Tämä kenttä sisältää kaikki numerot, jotka ovat tuotteita ja summia $\sqrt{2}$ ja $\sqrt{2}$. Nämä ovat muotoa $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. Mikä on aste $\big{2}, \sqrt{2}]: \mathbb Q{2}]\big]$?

Yes! Meillä on todellakin $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}^2+b\sqrt{2}+c) $ + $ (d\sqrt{2}^2 + e\sqrt{2} ^ 2 + e \sqrt{2} + F) \sqrt{2}$. Täten mikä tahansa luku $\mathbb Q{2},\sqrt{2}]$ voidaan kirjoittaa $A+B\sqrt{2}$, Missä $A$ ja $b$ kuuluvat $\mathbb Q{2}]$. Siten 2 skalaaria $\mathbb Q{2}]$ määrittää luvun $\mathbb Q{2},\sqrt{2}]$. Tämä tarkoittaa, että kentän laajennuksen $\mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ aste on 2. Itse asiassa meillä on Chaslesin suhde $\big{2}, \sqrt{2}]: \mathbb Q \big] $ = $ \big{2}, \sqrt{2}] : \mathbb Q{2}] \big] \big{2}]: \mathbb Q \big] $ = $ 2 \times 3 = 6$.

It ’ s better than that! Jokainen äärellisen asteen kenttälaajennus, jota kutsutaan äärelliseksi kenttälaajennukseksi, ulottuu yhdellä numerolla. Esimerkiksi $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, mikä tarkoittaa, että kaikki numerot, jotka ovat summia potensseista $\sqrt{2}$ ja $\sqrt{2}$, ovat myös summia potensseista $\sqrt{2} + \sqrt{2}$. Eikö ole yllättävän mahtavaa?

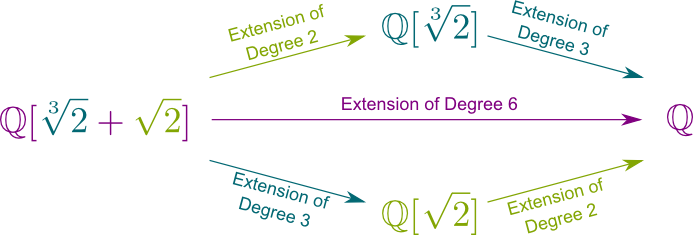
yleisemmin mikä tahansa rajallinen kenttälaajennus $\mathbb Q$ voidaan kirjoittaa $\mathbb Q$ jollakin $x$, joka lisätään $\mathbb Q$.

Kyllä. Kyseessä on kentän laajennus $\mathbb R / \mathbb Q$. Ja, niin on tärkein alan laajennus Galois teoriassa! Tämä kentän laajennus on $\bar {\mathbb Q} / \mathbb Q$, jossa $\bar {\mathbb Q}$ on algebrallisten lukujen joukko. Nämä ovat kaikki ratkaisuja polynomiyhtälöille, jotka ovat muotoa $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $+$ a_0 = 0$. Esimerkiksi $\sqrt{2}$ on algebrallinen luku, koska se on ratkaisu $x^4 – 2x = 0$. Täten $\bar {\mathbb Q}$ on kenttälaajennus kaikille $\mathbb Q$: n äärellisille kenttälaajennuksille.

Konjugaattiluvut

olemme melkein perillä! Tarvitsemme lopullisen kiertotien polynomiyhtälöiden avulla.

täsmälleen! Galois huomasi, että joitakin yhtälöitä voitiin yksinkertaistaa. Esimerkiksi $x^4-2x=0$ voidaan factorized as $x(x^3-2)=0$, joka vastaa $x=0$ tai $X^3-2=0$. Yhtälö $x^4-2x=0$ voidaan siis pienentää yhtälöihin $x=0$ ja $X^3-2=0$. Ja itse asiassa, tämä vähennys on hyvin samanlainen kuin miten numerot kuten 35 voidaan vähentää 5 ja 7, koska $5 \kertaa 7 = 35$. Yhtälöiden ja kokonaislukujen yhtäläisyys on niin vahva, että voimme tehdä jopa Euklidisia jakoja polynomeista, aivan kuten sinä olet oppinut tekemään sen luvuille! Oikealla on esimerkki tällaisesta jaosta (älä huoli, jos et ymmärrä sitä, se ei ole tärkeää jatko-osalle).

täsmälleen! Näitä kutsutaan irreduktiivisiksi polynomiyhtälöiksi. Yhtälö $x^3-2=0$ on esimerkki irreducible polynomiyhtälöstä.

Yes! Mutta ratkaisevasti, Galois halusi keskittyä yhtälöt järkevä kertoimia. Tai pikemminkin polynomit, joiden kertoimet kuuluvat peruskenttään. Niin, mitä tarkoitin, että $\mathbb Q$ peruskenttänä, $X^3-2=0$ on irreducible.

tarkastellaan $x^2 – 2x -1=0$, jotta saadaan joitakin vihjeitä. Tämä yhtälö voidaan todistaa irreducible. Muistatko, miten se ratkaistaan?

Jos $B^2-4ac \geq 0$, Kyllä.

täsmälleen! Joten, irreducible polynomi yhtälö $x^2 + 2x -1 = 0$ on kaksi ratkaisua: $1 + \sqrt{2}$ ja $1 – \sqrt{2}$ … mitään kommenttia?

Bingo! Se on Galois ’ n avainlöytö. Yleisemmin, Galois kutsutaan konjugates kaikki ratkaisut irreducible polynomi yhtälö. Ja kuten voitte kuvitella, nämä ovat välttämättömiä radikaalien poistamiseksi nimittäjistä!

ensimmäinen asia on huomata, että jos $x_1$, $x_2$,…, $x_n$ ovat kaikki ratkaisut polynomin irreducible yhtälö $a_n X^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ rationaalisilla kertoimilla, niin tämä polynomin irreducible yhtälö voidaan kirjoittaa uudelleen $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. Vakioehtojen tunnistaminen tuottaa tällöin $x_1 x_2 … x_n $ = $ (-1)^n a_0 / a_n$. Niinpä, ratkaisevasti, konjugaattilukujen tulo on Rationaaliluku $(-1)^n a_0/a_n$, joka on ei-nolla (todista se!).

tässä pieni vitsi pitää mielessä konjugaattien vahva yhteys:

tarkastellaan murtolukua $1 / x_1$, jossa $x_1$ on monimutkainen lauseke radikaaleilla. Kertomalla ylös ja alas konjugaatit $x_2$,…, $x_n$ of $x_1$ sitten tuottaa $1/x_1 $=$ (-1)^n a_n x_2…x_n / a_0$, joka ei ole radikaali nimittäjä, koska olemme vahvistaneet $a_0$ olla ei-nolla numero peruskentän!

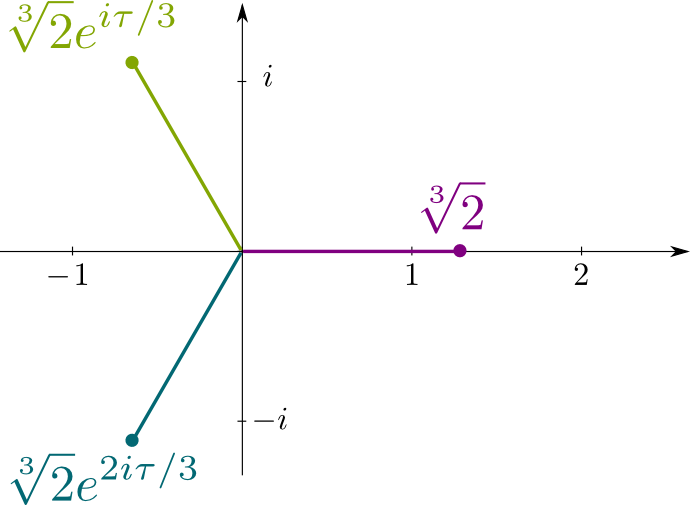
muista, että $X^3-2 = 0$ on irreducible polynomiyhtälö $\sqrt{2}$ on ratkaisu. Sen konjugaatit ovat siis muita ratkaisuja tähän yhtälöön, jotka ovat kompleksiluvut $\sqrt{2}j$ ja $\sqrt{2}J^2$, Missä $j= e^{i\tau/3}$, jossa $\tau = 2\pi$ on ympyrän kehän suhde sen säteellä. Seuraavassa kuvassa on esitetty konjugaattiliuosten sijainnit tässä kompleksitasossa:

Galois’ n monitulkintaisuus

vihdoin päästään Galois ’ n keskeiseen oivallukseen!

konjugaatit ovat täysin permisiä. Tämä tarkoittaa sitä, että jos systemaattisesti muuttaa $\sqrt{2}$ sen konjugaatilla $ – \sqrt{2}$, niin equalities pitää edelleen. Esimerkiksi, koska meillä oli $1/(\sqrt{2}-1) = \sqrt{2}+1$, voin suoraan sanoa, että $1 / (- \sqrt{2}-1)=-\sqrt{2}+1$! Vastaavasti meillä on seuraava tyrmäävä seuraus:

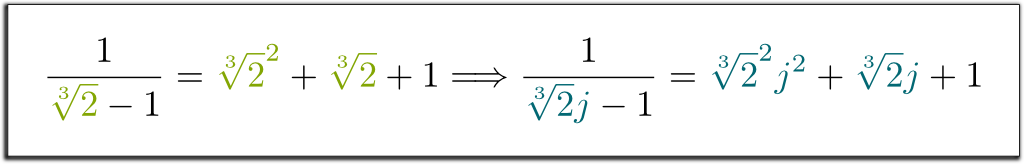
Hehe… haluan ensin muistuttaa, että äärelliset kentät ovat yhden elementin ulottamia. Joten, jos peruskenttä on $\mathbb Q$, Mikä tahansa äärellinen kenttä voidaan kirjoittaa $\mathbb Q$ jollekin oikealle $x_1$. Nyt, harkitse $X^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ irreducible polynomiyhtälö $x_1$ on ratkaisu. Sitten, mikä määrittelee $\mathbb Q$ on $\mathbb Q$ – vektoriavaruus, jota käytetään $ x_1$, $x_1^2$,…, $x_1^{n-1}$, yksinkertaistaen suurempia voimia $x_1$ vastaavasti algebrallinen sääntö $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

täsmälleen! Ratkaisevaa on, että nämä algebralliset säännöt $\mathbb Q$ eivät oikeastaan riipu luonteesta $x_1$; ne riippuvat vain irreducible polynomi $x_1$ on ratkaisu! Siksi $\mathbb Q$: n säännöt ovat samat kuin $\mathbb Q$, …, $\mathbb Q$, jossa $x_1$ korvataan jollakin sen konjugaateista $x_2$, …, $x_n$. Erityisesti kentät $\mathbb Q{2}]$ ja $\mathbb Q{2} j]$ toimivat täsmälleen samojen sääntöjen mukaisesti. Siksi konjugaatit ovat täysin permitoituvia! Sanomme, että kentät $\mathbb Q{2}]$ ja $\mathbb Q{2} j]$ ovat isomorfisia, ja että $\sqrt{2}$: n korvaaminen $\sqrt{2}$: lla on isomorfismi $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

hyvin samanlaisella (mutta voimakkaammalla) tavalla, että kaksi ulottuvuuden 2 vektoriavaruutta ovat kutakuinkin samat! Tällä on hirvittävät seuraukset. Se tarkoittaa, että algebrallisesta näkökulmasta on merkityksetöntä tehdä ero numeron ja minkä tahansa sen konjugaatin välillä (kunhan järjestelmällisesti korvaa luvun sen konjugaatilla)! Esimerkiksi $\sqrt{2}$ ja $ – \sqrt{2}$ ovat algebrallisesti erottamattomia! Pitääkseni tämän mielessä, tässä on toinen vitsi olen keksinyt:

Ei ollenkaan! Näiden kahden luvun väliseen eroon on liityttävä jokin muu matematiikka kuin algebra, kuten järjestyssuhteet tai topologia. Tarkoitan, että esimerkiksi relaatio $\sqrt{2} > 0$ tekee eron $\sqrt{2}$ by $-\sqrt{2}$, mutta se johtuu siitä, että siihen liittyy järjestysrelaatio. Mutta jos rajoitumme polynomifunktioihin, ei ole mitään eroa $\sqrt{2}$: n ja $-\sqrt{2}$: n välillä. Vastaavasti $i$ ja $ – I$, irreducible polynomiyhtälön $x^2+1=0$ ratkaisut ovat myös algebrallisesti erottamattomia. Silti me sanomme mielivaltaisesti $i$ yksi niistä. Tämän vuoksi Galois kutsui teoriaansa monitulkintaisuuden teoriaksi. Tänään, epäselvyyttä valinta perinteisen neliöjuuri $-1$ joukossa $i$ ja $ – I$ kutsutaan symmetria välillä $i$ ja $ – I$.

Galois ’ n ryhmät

Galois keskittyi erityisesti kenttälaajennuksiin, jotka ovat vakaita konjugaatiolla. Tällaisia vakaita kenttälaajennuksia kutsutaan nykyään Galois ’ n laajennuksiksi. Joten, jos $x_1$ kuuluu Galois laajennus, niin tämä Galois laajennus sisältää kaikki sen konjugaatit $x_2$,…, $x_n$.

yksinkertainen tapa konstruoida Galois ’ n laajennukset on ottaa kenttä, joka ulottuu irreduktiivisen polynomiyhtälön ratkaisuilla. Esimerkiksi jos $x_1$,…, $x_n$ ovat konjugaatteja peruskentälle $\mathbb Q$, niin $\mathbb Q / \mathbb Q$ on Galois ’ n laajennus. Näin rakennettuja kenttiä kutsutaan halkaisukentiksi.

esimerkiksi yhtälön $x^3-2=0$ jakokenttä on Galois ’ n laajennus $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} J^2] / \mathbb Q$, jota sen ratkaisut ulottuvat.

Jos $x_1$ ulottuu Galois ’ n laajennukseen, niin tekevät myös sen konjugaatit. Niinpä $\mathbb Q = \mathbb Q = $ … $ = \mathbb Q$ = $\mathbb Q$. Näin ollen isomorfismi $\mathbb Q$: n ja $\mathbb Q$: n välillä, joka koostuu aina $x_1$: n korvaamisesta $x_2$: lla, on itse asiassa isomorfismi $\mathbb Q$: n ja itsensä välillä! Kutsumme sitä automorfismiksi. Galois ’n laajennuksen automorfismit $\mathbb Q/\mathbb Q$ muodostavat Galois’ n ryhmän $Gal(\mathbb Q/\mathbb Q)$.

nyt ratkaisevasti, jos $\mathbb Q = \mathbb Q$, niin kaikki Galois ’ n laajennuksen automorfismit $\mathbb Q / \mathbb Q$ ovat permutaatioita $x_1$ yhdellä sen konjugaateista! Erityisesti näemme tässä, että cardinality, Galois ryhmä on yhtä suuri kuin aste, Galois laajennus.

varma! Voit huomata, että $\mathbb Q = \mathbb Q$ ja $\mathbb Q = \mathbb Q$, mikä tarkoittaa, että $i$ ja $\sqrt{2}$ kumpikin ulottuu sen irreducible polynomiyhtälön halkaisukentille, jonka ne ovat ratkaisu. Täten $\mathbb Q / \mathbb Q$ ja $\mathbb Q / \mathbb Q$ ovat molemmat Galois ’ n laajennuksia. Siksi niiden automorfismit koostuvat $i$: n korvaamisesta jollakin sen konjugaateista, $i$: lla tai $-I$: lla, ja $\sqrt{2}$: n korvaamisesta $\sqrt{2}$: lla tai $-\sqrt{2}$: lla. Ensimmäisissä tapauksissa emme muuta mitään luvuiksi, mikä vastaa nollasymmetriaa. Jälkimmäiset tapaukset voidaan visualisoida aksiaalisina symmetrioina, kuten alla olevasta kuvasta näkyy:

eikö ole hämmästyttävää?

varma! Siirrytään jakokenttään $\mathbb Q{2},\sqrt{2}j, \sqrt{2}J^2]$ of $x^3-2=0$. Mutta ennen kuin jatkamme pidemmälle, huomatkaamme, että $\mathbb Q{2},\sqrt{2}j, \sqrt{2}J^2] = \mathbb Q{2}, j]$.

kaikki mitä meidän tarvitsee todistaa on, että kaikki generaattorit yhden kentän kuuluu muille. Aloitetaan osoittamalla, että jälkimmäisen generaattorit $\sqrt{2}$ ja $j$ kuuluvat edelliseen. Se on ilmeistä $ \sqrt{2}$. Nyt $j = (\sqrt{2} j) / \sqrt{2}$, jolloin $j$ kuuluvat myös entiseen kenttään. Tämä todistaa,että kaikki elementit $\mathbb Q{2}, j]$ kuuluvat $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} J^2]$. Vastavuoroisesti on selvää, että kaikki edellisen kentän generaattorit, $\sqrt{2}$, $\sqrt{2}j$ ja $\sqrt{2}J^2$, ovat jälkimmäisen generaattorin tuotteita. Näin ollen molemmat kentät ovat yhtä suuret. Ja erityisesti $\mathbb Q{2}, j] / \mathbb Q$ on Galois ’ n laajennus.

Hehe… ymmärtääksemme $\mathbb Q{2}]$: n symmetrioita, meidän on mentävä pidemmälle Galois’ n tutkimuksessa Galois ’n ryhmistä…

Galois’ n kirjeenvaihdosta

Galois ’ n ryhmien ongelmana on, että niistä voi tulla äärimmäisen suuria ja monimutkaisia. Tämä koskee erityisesti ääretöntä ryhmää $Gal (\bar{\mathbb Q}/\mathbb Q)$. Saadakseen kiinni niin valtavia ja monimutkaisia ryhmiä, Galois oli loistava idea rikkoa nämä pienemmiksi paloiksi.

hämmästyttävästi Galois sai selville, että Galois ’ n ryhmät voitiin jakaa symmetrioiden alaryhmiksi tarkastelemalla vain niitä, jotka jättävät jonkin alikentän ennalleen. Esimerkiksi $\mathbb Q$ on $\mathbb Q{2},j]$: n alikenttä, koska mikä tahansa edellisen luku kuuluu jälkimmäiseen. Täten symmetriat $\mathbb Q{2},j]$, jotka eivät muuta mitään $\mathbb Q$, muodostavat Galois ’ n ryhmän aliryhmän $\mathbb Q{2}, j]/\mathbb Q$. Nämä symmetriat muodostavat Galois ’ n ryhmän $Gal(\mathbb Q{2},j]/\mathbb Q)$.

tiedän! Haluan visualisoida nämä symmetriat tapoina kytkeä $\mathbb Q{2}, j]$ päälle $\mathbb Q$. Tässä on imagoitu kuva ”plugging on”:

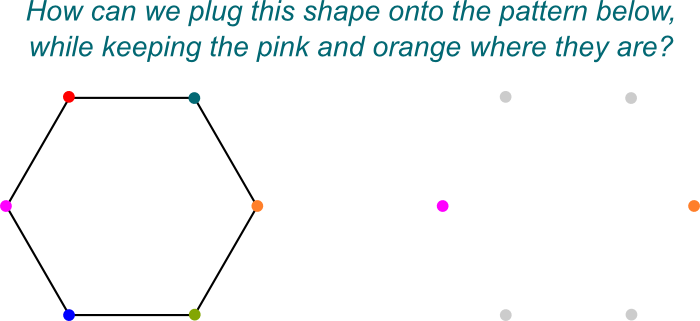
täsmälleen! Ja se johtuu yksinkertaisesti siitä, että $\mathbb Q{2}, j]$ on Galois ’ n laajennus $\mathbb Q$, joka itsessään on kentän laajennus $\mathbb Q$.

And there ’ s more! Galois osoitti, että kaikki alaryhmiä, Galois laajennukset saadaan tällä tavalla! Tarkemmin sanottuna minkä tahansa kentän $k$ yhdistäminen Galois ’n laajennuksen $\mathbb Q{2},j]$ ja peruskentän $\mathbb Q$ väliin Galois’ n ryhmään $Gal(\mathbb Q{2},j] / K)$ on bijektiivinen. Tämä tosiasia on nimeltään Galois kirjeenvaihto! Tämä kirjeenvaihto näytetään kaavamaisesti alla Galois-laajennukselle $\mathbb Q / \mathbb Q$.

sen sijaan, että yrittäisimme kuvata tätä ryhmää suoraan, keskitytään sen alaryhmään $Gal(\mathbb Q{2}, j] / \mathbb Q)$. On selvää,että $\sqrt{2}$ ulottuu $\mathbb Q{2}, j]$ kun lisätään $\mathbb Q$. Näin ollen $\mathbb Q{2},j]/\mathbb Q$ on Galois ’ n laajennus, joka ulottuu $\sqrt{2}$. Tämän vuoksi, käyttämällä aiemmin näkemäämme teoreemaa, tiedämme, että kaikki tämän Galois ’ n laajennuksen automorfismit korvaavat $\sqrt{2}$ yhdellä sen 3 konjugaatista (itse $\sqrt{2} j$ ja $\sqrt{2} J^2$)!

nyt voisin jatkaa muiden $Gal(\mathbb Q{2}, j]/\mathbb Q)$: n kappaleiden tutkimista, kuten Galois ’ n alaryhmä $Gal(\mathbb Q{2}, j] / \mathbb Q{2}])$. Mutta aion mieluummin käyttää toinen Galois ’ voimakas teoreemojen. Nimittäin, hän osoitti, että jos $\mathbb Q / \mathbb Q$ oli lisäksi Galois laajennus itse, niin aliryhmä $Gal (\mathbb Q{2}, j] / \mathbb Q)$ on normaali.

näin Galois ’ n ryhmä $\mathbb Q{2}, j]/\mathbb Q$ voidaan osittaa tällä alaryhmällä,ja osamäärä ryhmä on tällöin $Gal(\mathbb Q / \mathbb Q)$. Silti $\mathbb Q / \mathbb Q$ On todellakin Galois ’ n laajennus, jota ulottuu $j$, jonka konjugaatti on $J^2$. Täten $Gal (\mathbb Q/\mathbb Q)$ tarkoittaa joko $j$: n jättämistä $j$: ksi tai sen korvaamista $J^2$: lla.

voimme nyt päätellä kaikki symmetriat $Gal(\mathbb Q{2},j] / \mathbb Q)$ yhdistämällä nämä $Gal(\mathbb Q{2},j]/\mathbb Q)$ ja $Gal(\mathbb Q / \mathbb Q)$. Voimme näyttää nämä symmetriat piirtämällä, miten ne vaikuttavat kolmeen konjugaattiimme $\sqrt{2}$, $\sqrt{2}j$ ja $\sqrt{2}J^2$:

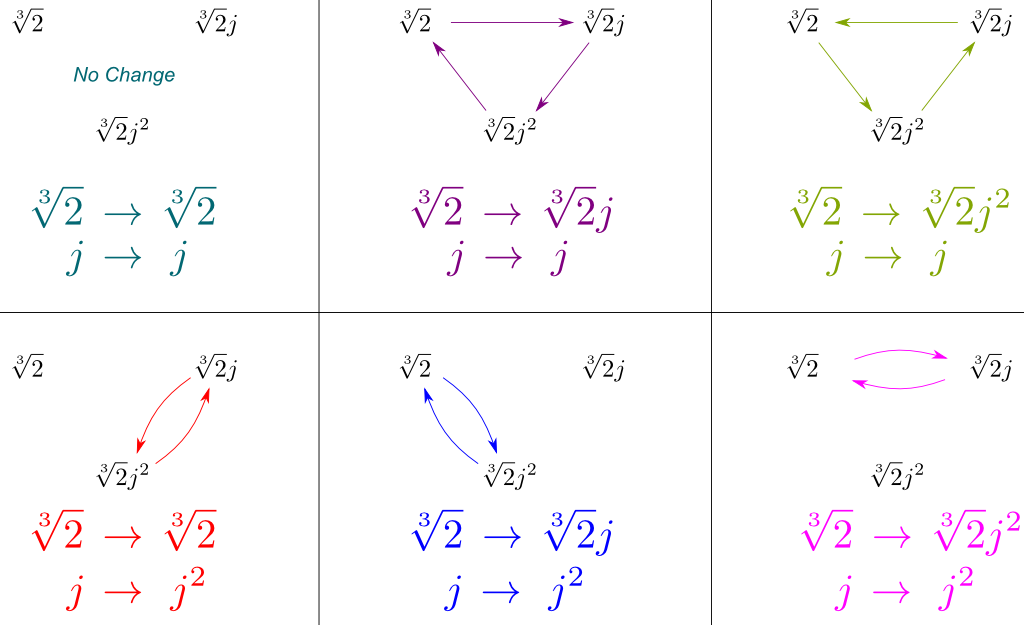
yllä oleva luku sisältää kaikki symmetriat $Gal(\mathbb Q{2}, j] / \mathbb Q)$. Ja hämmästyttävää kyllä, nämä symmetriat vastaavat tunnettua symmetriaryhmää.

i ’ ll let Marcus du Sautoy present it to you:

ovatko symmetriat tässä kuin meritähti vai kolmio?

kyllä, todellakin! Tätä kolmion symmetrioiden ryhmää kutsutaan nimellä $D_3$, ja se on sama kuin 3 elementin permutaatioiden ryhmää $S_3$. Tämä johtaa meidät seuraavaan kaavaan, joka oli mielestäni niin kaunis, että olen päättänyt kehystää sen!

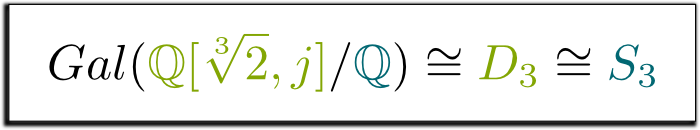
voidaan päätellä

monin tavoin, että Galois’ ta on pidettävä modernin algebran isänä. Hänen keskeinen oivallus oli tarkastella matematiikan kautta kulma sääntöjen toimintaa, ja tämä johti hänet paljastaa yllättäviä ja oivaltava epäselvyyksiä, tai symmetries, välillä numerot. Algebrallisesta näkökulmasta luvut kuten $\sqrt{2}$, $\sqrt{2}j$ ja $\sqrt{2}J^2$ ovat todellakin täysin symmetrisiä ja täysin vaihdettavissa.

näiden symmetrioiden ymmärtämisellä on ollut hämmästyttäviä sovelluksia muun muassa algebrallisessa geometriassa ja algebrallisessa topologiassa. Teorian varhaisiin menestyksiin kuuluvat erityisesti konstruoitavien säännöllisten monikulmioiden luokittelu ja lause, jonka mukaan korkean asteen polynomiyhtälöitä ei voitu ratkaista radikaaleilla.

Viimeaikaiset onnistumiset näkyvät kryptografiassa ja Andrew Wilesin todisteena Fermat’ n suuresta lauseesta. Tämä todiste edellyttää Galois ’ n ryhmän $Gal(\bar{\mathbb Q} /\mathbb Q)$ tutkimista ryhmäesityksellä. Mutta sanoisin, että teoria on jotenkin vielä nuori,ja paljon on vielä selvitettävää. Onhan se yksi aktiivisimmista tutkimusalueista nykypäivän puhtaan matematiikan tutkimuksessa.

tämän pitäisi johtaa meidät maksamaan paljon enemmän kunnianosoituksia Galois’ unbelievable genius… Let me include one by SocraticaStudios.