joissakin olosuhteissa toroidaalisen Kelan käämityksessä oleva virta vaikuttaa vain käämien sisällä olevaan B-kenttään eikä vaikuta käämien ulkopuolella olevaan magneettiseen B-kenttään. Tämä on seurausta symmetriasta ja Ampèren ympyrälaista.

riittävät edellytykset B-fieldeditin täydelliselle sisäsäilytykselle

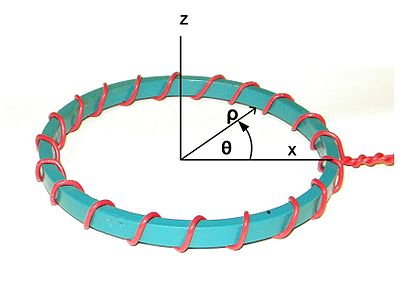
kuva. 1. Koordinaattijärjestelmä. Z-akseli on symmetrian nimellinen akseli. X-akseli valitaan mielivaltaisesti riviin käämityksen alkupisteen kanssa. ρ kutsutaan säteittäinen suunta. θ: tä kutsutaan kehäsuunnaksi.

Fig. 2. Aksiaalisesti symmetrinen toroidaalinen induktori, jossa ei ole kehävirtaa.

kehävirran puuttuminen (kehävirran kulkureitti on merkitty punaisella nuolella tämän jakson kuvassa 3) ja johtimien ja magneettisten materiaalien aksiaalisesti symmetrinen sijoittelu ovat riittävät edellytykset B-kentän täydelliselle sisäiselle vangitsemiselle. (Jotkut kirjoittajat käyttävät mieluummin h-kenttää). Symmetrian vuoksi B-vuon viivojen on muodostettava symmetria-akselille keskitettyjä vakionvoimakkuuden ympyröitä. Ainoat B-vuon linjat, jotka ympäröivät mitään virtaa, ovat ne, jotka ovat toroidisen käämin sisällä. Siksi Amperen circuital laista B-kentän voimakkuuden on oltava nolla käämien ulkopuolella.

Fig. 3. Toroidaalinen induktori, jonka kehävirta on

tämän osan Kuvassa 3 on yleisin toroidinen käämi. Se ei täytä kaikkia B-kenttäsäilytystä koskevia vaatimuksia. Akselilta katsottuna käämi on joskus ytimen sisäpuolella ja joskus ytimen ulkopuolella. Se ei ole aksiaalisesti symmetrinen Lähialueella. Kuitenkin pisteissä etäisyys useita kertoja käämien väli, toroid ei näytä symmetrinen. Kehävirran ongelma on edelleen olemassa. Ei ole väliä kuinka monta kertaa käämitys ympäröi ydin ja riippumatta siitä, kuinka ohut lanka, tämä toroidinen induktori sisältää edelleen yhden kelan silmukan toroidin tasossa. Tämä käämitys tuottaa myös ja ovat alttiita e-kentän tasolla Kelan.

luvut 4-6 esittävät erilaisia tapoja neutraloida kehävirtaa. Kuva 4 on yksinkertaisin ja on se etu, että return wire voidaan lisätä sen jälkeen, kun induktori on ostettu tai rakennettu.

Fig. 4. Kehävirta torjutaan paluujohdolla. Lanka on valkoinen ja kulkee Kelan ulkoreunan ja Kelan ulomman osan välillä.

Fig. 5. Kehävirta torjutaan paluukäämityksellä.

Fig. 6. Kehävirta kumoutui halkaistulla paluukäämityksellä.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

potentiaali jakaantuu pitkin käämiä. Tämä voi johtaa e-kenttään tasolla toroid ja myös alttius e-kenttään tasolla toroid kuten kuvassa 7. Tätä voidaan vähentää käyttämällä paluukäämitys kuten kuvassa 8. Tämän käämityksen, jokainen paikka käämitys ylittää itsensä, kaksi osaa on yhtä ja vastakkainen napaisuus, joka vähentää merkittävästi e-kentän syntyy tasossa.

toroidinen induktori/muuntaja ja magneettinen vektoripotentiaali

osoittaa magneettisen vektoripotentiaalin kehittymisen symmetrisen toroidisen induktorin ympärille.

Katso Feynmanin luvuista 14 ja 15 Yleinen keskustelu magneettisesta vektoripotentiaalista. Katso Feynmanin sivuilta 15-11 kaavio pitkän ohuen solenoidin ympärillä olevasta magneettisesta vektoripotentiaalista, jossa esiintyy myös B-kentän täydellinen sisäinen koppi, ainakin äärettömässä rajassa.

a-kenttä on tarkka käytettäessä oletusta B f A = 0 {\displaystyle bf{a}=0}

. Näin olisi seuraavien oletusten mukaan:

• 1. Coulombin mittaria käytetään
• 2. Lorenzin mittaria käytetään, eikä varausjakaumaa ole, ρ = 0 {\displaystyle \rho =0\,}
  
• 3. käytetään Lorenzin mittaria ja nollataajuudeksi oletetaan
• 4. käytetään Lorenz-mittaria ja oletetaan, että nollataajuus on niin alhainen, että 1 C 2 ∂ ϕ ∂ T {\displaystyle {\frac {1}{C^{2}}}{\frac {\partial \Phi }{\partial t}}}
  

  .

luvun 4 oletetaan olevan tämän osan loppuosassa ja siihen voidaan viitata ”kvasistaattisessa tilassa”.

vaikka aksiaalisesti symmetrinen toroidinen induktori, jossa ei ole kehävirtaa, rajoittaa B-kentän kokonaan käämien sisälle, A-kenttä (magneettinen vektoripotentiaali) ei ole rajoitettu. Nuoli #1 kuvaa vektoripotentiaalia symmetria-akselilla. Säteittäiset virtaosat a ja b ovat yhtä kaukana akselista, mutta osoittavat vastakkaisiin suuntiin, joten ne kumoavat. Samoin segmentit c ja d peruuttavat. Itse asiassa kaikki säteittäiset nykyiset segmentit peruuttavat. Aksiaalivirtausten tilanne on toinen. Toroidin ulkopinnan aksiaalivirta osoittaa alaspäin ja sisäpuolen aksiaalivirta ylöspäin. Jokainen aksiaalinen virtasegmentti toroidin ulkopuolella voidaan sovittaa yhtä suureen mutta vastakkaisesti suunnattuun janaan toroidin sisäpuolella. Segmentit sisäpuolella ovat lähempänä kuin segmentit ulkopuolella akseliin, joten on olemassa net ylöspäin komponentti a-kentän pitkin akselin symmetria.

edustavat magneettista vektoripotentiaalia (A), magneettivuo (B) ja virrantiheyttä (j) ympäröiviä kenttiä poikkileikkaukseltaan ympyrän muotoisen toroidisen Kelan ympärillä. Paksummat viivat osoittavat kenttäviivoja, joiden keskimääräinen voimakkuus on suurempi. Ytimen poikkileikkauksessa olevat ympyrät edustavat kuvasta poistuvaa B-vuota. Plusmerkit ytimen toisessa poikkileikkauksessa kuvaavat kuvaan menevää B-vuota. Div A = 0 on oletettu.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ T → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

(kuten olisi tuotettu toroidinen induktori ) on laadullisesti sama kuin B kentän ympärillä silmukka nykyisen. Kuvassa vasemmalla on taiteilijan kuvaus toroidisen Kelan ympärillä olevasta a-kentästä. Paksummat viivat ilmaisevat polkuja, joiden keskimääräinen voimakkuus on suurempi (lyhyemmillä poluilla on suurempi intensiteetti niin, että polkuintegraali on sama). Viivat on vain piirretty näyttämään hyvältä ja antamaan a-kentän yleisilmettä.

Toroidimuuntajan toiminta B: n kokonaispotentiaalin läsnä ollessa

e-ja B-kentät voidaan laskea A: sta ja ϕ {\displaystyle \phi \,}

(skalaarisähköpotentiaali) kentistä B = ∇ × A . {\displaystyle \mathbf {b} = \nabla \times \mathbf {a} .}

and : e = − ∇ ϕ − ∂ A ∂ T {\displaystyle \mathbf {e} =-\nabla \Phi -{\frac {\partial \mathbf {A} }{\partial t}}}

ja niinpä vaikka käämien ulkopuolisella alueella ei olisi b-kenttää, se täytetään ei-nolla-e-kentällä. Suure ∂ a ∂ t {\displaystyle {\frac {\partial \mathbf {a} }{\partial t}}}

on vastuussa toivottavasta magneettikentän kytkemisestä primäärin ja sekundäärin välillä, kun taas Suure ∇ ϕ {\displaystyle \nabla \Phi\,}

on vastuussa ei-toivotusta sähkökenttäkytkennästä primäärisen ja sekundäärisen välillä. Muuntajan suunnittelijat pyrkivät minimoimaan Sähkökentän kytkennän. Loppuosan osalta ∇ ϕ {\displaystyle \ nabla \ Phi\,}

oletetaan olevan nolla, ellei toisin mainita.

Stokesin lause pätee siten, että A: n polkuintegraali on yhtä suuri kuin suljettu B vuo, samoin kuin polkuintegraali B on yhtä suuri kuin Vakio kertaa suljettu virta

E: n polkuintegraali toisiokäämiä pitkin antaa toision indusoiman EMF: n (Elektro-Motive Force).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

which sanoo EMF on yhtä suuri kuin aikanopeus muutoksen b Flux suljettu käämi, joka on tavanomainen tulos.

Toroidimuuntajan Poynting-vektorikytkentä primääristä sekundaariin B-kentän kokonaiskontaminaation läsnä ollessa

tässä kuvassa, siniset pisteet osoittavat, missä b-vuo primaarivirrasta tulee ulos kuvasta ja plus-merkit osoittavat, missä se menee kuvaan.

Kuvan selitys

tässä kuvassa näkyy toroidimuuntajan puolisko. Kvasistaattiset olosuhteet oletetaan, joten jokaisen kentän vaihe on kaikkialla sama. Muuntaja, sen käämit ja kaikki asiat jakautuvat symmetrisesti symmetria-akselin suhteen. Käämit ovat sellaiset, ettei kehävirtaa ole. Vaatimukset täyttyvät B-kentän täydelliselle sisäiselle vangitsemiselle primäärivirran vuoksi. Ydin-ja ensiökäämiä edustaa harmaanruskea torus. Ensiökäämiä ei näytetä, mutta poikkileikkauspinnan käämin virta esitetään kultaisina (tai oransseina) ellipseinä. Primäärivirran aiheuttama B-kenttä rajoittuu kokonaan ensiökäämin rajaamaan alueeseen (eli ytimeen). Siniset pisteet vasemmassa poikkileikkauksessa osoittavat, että ytimen B-vuon viivat tulevat ulos vasemman käden poikkileikkauksesta. Toisessa poikkileikkauksessa siniset plus-merkit osoittavat, että B-vuo tulee sinne. Primaarivirtauksista peräisin oleva e-kenttä näkyy vihreinä ellipseinä. Toisiokäämi näkyy ruskeana viivana, joka tulee suoraan symmetria-akselia alaspäin. Normaalissa käytännössä sekundäärisen kaksi päätä on kytketty yhteen pitkällä langalla, joka pysyy hyvin kaukana toruksesta, mutta absoluuttisen aksiaalisen symmetrian säilyttämiseksi koko laitteen kuvitellaan olevan täysin johtavan pallon sisällä, jossa toissijainen johto on ”maadoitettu” pallon sisäpuolelle kummassakin päässä. Toissijainen on valmistettu vastuslangasta, joten erillistä kuormaa ei ole. E-kenttä sekundäärissä aiheuttaa virran sekundäärissä (keltaiset nuolet), joka aiheuttaa B-kentän sekundäärin ympärille (näytetään sinisinä ellipseinä). Tämä B-kenttä täyttää tilan, myös muuntajan ytimen sisällä, joten lopulta on jatkuva nollasta poikkeava B-kenttä primaarista sekundaariin, jos toisio ei ole avoin piiri. E-kentän (johdettu primäärivirtauksista) ja B-kentän (saatu sekundäärivirtauksista) ristitulo muodostaa Poynting-vektorin, joka osoittaa primaarista kohti sekundääristä.