olennainen osa fluididynamiikkaa on vortiittisuus. Heuristisesti se mittaa nestelohkon paikallista kiertoa. Kiinteiden esineiden emme puhu vorticity, esine, vaan viittaamme sen kulmanopeus. Nämä kaksi käsitettä liittyvät toisiinsa, mutta vortiittisuus on hyödyllisempää puhuttaessa pyörivistä kappaleista, jotka muuttavat muotoaan, kuten fluidi tekee.

tietyn nopeuskentän vortiittisuus tietyllä tasolla lasketaan valitsemalla mikä tahansa kyseisen tason kaksi ortogonaalista akselia ja lisäämällä kunkin akselin kulmanopeus. Kiinteässä kappaleessa, tai fluidissa, joka pyörii kuin kiinteä kappale (osuvasti nimetty kiinteän kappaleen kierto), pyörimisnopeus on kaksi kertaa kulmanopeus, koska jokainen akseli pyörii samalla nopeudella. Kuitenkin nesteen kaksi akselia voi pyöriä hyvin eri nopeudella ja jopa eri suuntiin! On jopa mahdollista, että jokainen akseli voi pyöriä, mutta netto vorticity on nolla (KS.irrotational vortex).

Jos fluidin liike rajoittuu tiukasti tasoon, niin vortiittivektorin katsotaan olevan tason ortogonaalinen eikä se voi muuttaa suuntaa (tai kallistaa). Ainoa osa vortiittisuutta, joka voi muuttua, on sen suuruus. Uskotaan, että tämä energian siirto suurempiin mittakaavoihin liittyy suuren punaisen täplän muodostumiseen Jupiteriin.

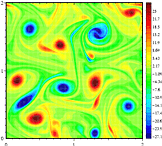
kolmiulotteisessa fluidiliikkeessä vortiittivektori on kolmiulotteinen siinä mielessä, että siinä on kunkin akselin, x: n, y: n ja z: n suuntaiset komponentit: Z-komponentti on Z-akselin suuntainen ja kuvaa pyörimisnopeutta xy-tasossa. Juuri tämän kahtiajaon vuoksi kaksiulotteisen turbulenssin ja kolmiulotteisen turbulenssin välillä on laadullinen ero käyttäytymisessä. Edellisessä on taipumus vortices paakkuuntua yhteen ja muodostaa suurempia vortices, kun taas jälkimmäisessä vortical liikkeet ovat repeytyneet ja energia cascades alas pienin asteikot, jossa se on sitten hajonnut pois.

matemaattisesti tietyn nopeuskentän vortiittisuus,

määritellään nopeuskentän kaareksi, ja sitä merkitään yleensä kreikkalaisella kirjaimella omega,

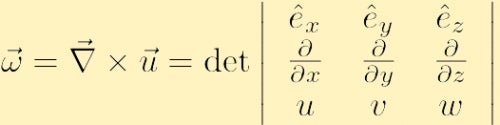
missä olemme käyttäneet perinteistä Nabla-symbolia Gradientille:

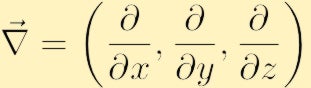
komponenttimuodossa vortiittisuus havaitaan yllä olevaa determinanttia laajentamalla,

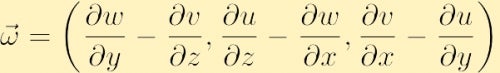
toinen vortiittisuuteen liittyvä tärkeä fluididynamiikan osa-alue on verenkierto. Toisin kuin vortiittisuus, joka on avaruuden jokaisessa pisteessä määritelty paikallinen ominaisuus, kierto on globaali ominaisuus, joka määritellään integroimalla fluidin ominaisuus käyrän yli. Erityisesti, jos valitaan jokin suljettu ääriviiva ja merkitään se kirjaimella C(t), kiertokulku C(t): n ympärillä vastapäivään, on skalaarisuure merkittynä,

määritellään seuraavasti:

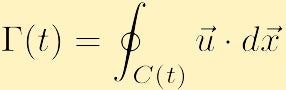
joka voi olla ajan funktio, kuten myös suljettu ääriviiva.

selitetäänpä hetki, mitä tämä fyysisesti sanoo. Jokaisessa pisteessä contourC (t) löydämme komponentin nopeus, joka on tangentti käyrä ja kerrotaan tämä skalaari on äärettömän pieni pituus; projisoimalla nopeus tangentti välttämättä antaa magnitudi välillä nopeus kyseisessä asennossa ja nolla. Jos nopeus on tangentti käyrä sitten saamme plus tai miinus nopeus, Jos nopeus on ortogonaalinen käyrä, saamme nolla. Sitten me integroida tämä määrä, eri tapa sanoa yhteen ääretön määrä asioita, ympäri ääriviivat niin, että lisäämme panoksen jokaisesta pisteestä. Tästä voimme päätellä, että kierto pitkin ääriviivat C (t) on määrä virtauksen ympäri contourC (t); positiivinen tai negatiivinen tulos vastaa ääriviivoja myötäpäivään tai myötäpäivään. Yksi ääritapaus on, jos nopeus kenttä on kaikkialla kohtisuorassa käyrä C (t) ja näin ollen ei ole liikkeeseen, koska virtaus on aina ylittää ääriviivat eikä koskaan virtaa pitkin ääriviivat. Saadakseen nonzero liikkeeseen on oltava jokin osa käyrä, jossa virtaus on pitkin suljettua ääriviivat.

Jos nopeuskenttä on sileä eikä C(t): n sisällä ole singulariteetteja, Voimme käyttää Stokesin Integraalilausetta vektorilaskennasta kierron uudelleenkirjoittamiseen,

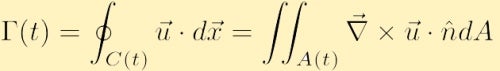
missä A on ympärysmitan C sisältämä pinta-ala ja µ on yksikön normaali vektori areaA.

ennen kuin mietitään tätä uutta liikkeeseen liittyvää yhtälöä, on hyödyllistä ymmärtää Stokesin lauseen fysikaalinen merkitys, Jossa vektorikenttä on nopeus. Vuonna kaksinkertainen integraali edellä me laskea vorticity jokaisessa pisteessä ääriviivat ja sitten tiivistää vorticity yli kaikki nämä kohdat (t). Vuonna yhden integraalin yli suljetun ääriviivat olemme computing virtaus pitkin rajaa alueella. Stokes lause sitten todetaan, että nämä suureet ovat yhtä, ja siten, että jos on olemassa keskiarvo vorticity sisällä alueella, joka on sitten tarkoita, että alue on nonzero pyörimisnopeus, on näin ollen oltava nettokiertoa pitkin kokoisen, että rajan.

calculuksen Keskiarvolauseesta voidaan korvata kaksoisintegraali integrand keskiarvolla, joka vastaa vortiittisuuden ortogonaalista keskiarvokomponenttia sille tasolle, jossa C(t) sijaitsee. Siten toinen tulkinta verenkierrosta on, että se on keskimääräinen vortiittisuus kertaa C(t): n sisältämä alue. Sen sijaan computing liikkeeseen suljetun ääriviivat C (t) voimme laskea keskimääräinen vorticity normaali(t) ja kerrotaan, että alueen sisällä. Jos ajatellaan erikoistapausta, jossa vortiittisuus on kaikkialla vakio, kierto olisi vortiittisuuden suuruus kertaa sen sisältämä alue.

pistepyörre on pyörre, jolla ei ole pinta-alaa, eli vortiittisuus esiintyy vain yhdessä pisteessä. Tutkia kohta vortices me ensin olettaa, että meillä on 2D incompressible virtaus. (Point vortices ovat myös joskus kutsutaan line vortices kun tarkastellaan 3D.)

joidenkin laskelmien jälkeen päätämme, että nopeuskenttä, joka syntyy kompleksisessa muodossa olevasta pistepyörteestä, joka sijaitsee Z0: ssä, on annettu (jossa Gamma nolla on pistepyörteen ympärillä oleva kierto, jota usein kutsutaan pistepyörteen vahvuudeksi):

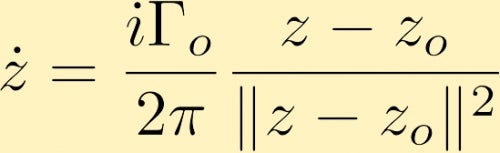
yhden pisteen pyörteen synnyttämä nopeuskenttä voi aiheuttaa toisen pistepyörteen liikkumisen. Tässä muutamia esimerkkejä tästä: Kahden pisteen vortices, molemmat positiivisia ja yhtä suuria, kahden pisteen vortices, molemmat positiivisia, mutta yksi on kolminkertainen vahvuus muiden ja yksi kohta vortex on negatiivinen kanssa kaksi kertaa suuruus muut, joka on positiivinen . Toinen mahdollisuus on tarkastella kahta samaa suuruusluokkaa olevaa, mutta vastakkaista merkkiä.

Tämä voidaan laajentaa mihin tahansa pistepyörteen määrään, N. kompleksimuodossa olevan liikkeen yhtälö pistepyörteen Alfalle saadaan:

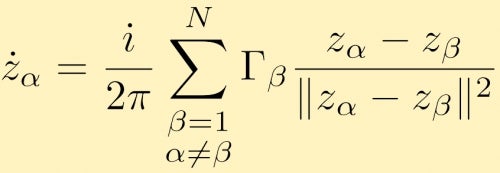
pisteiden pyörteiden vuorovaikutusten tarkasteleminen on hyvin mielenkiintoinen ongelma, jota on vaikea tehdä analyyttisesti varsinkin pisteiden pyörteitten lukumäärän kasvaessa. Numeeriset simulaatiot pistepyörteen vuorovaikutuksista ovat siis hyvin yleisiä. Yksi hyödyllinen sovellus suuri kohta vortex simulaatiot on, jos tarkastellaan suuria klustereita kohta vortices joka simuloi vortices rajallinen alue. Tässä on kuvauksia ja tuloksia useiden suurten pistepyörre simulaatioita. Tässä tapauksessa meillä on kaksi suurta klustereita kohta vortices yhtä vahva yhdistäminen. Seuraavassa tapauksessa aloitamme kanssa rengas klusteroitu kohta veracities.

löytääksemme yhtälön vortiittisuuden evoluutiolle aloitamme momenttiyhtälöllä. Momenttiyhtälössä advektiivinen termi voidaan kirjoittaa uudelleen seuraavasti:

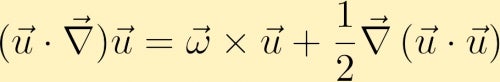
seuraavaksi lasketaan momenttiyhtälön käyrä ja joidenkin vektoriyhtälöiden kautta saadaan vortiittiyhtälö:

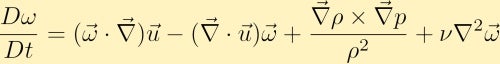
vortiittiyhtälö osoittaa, miten vortiittisuus voi syntyä fluidissa. Ilman yleisyyden menetystä oletamme, että aluksi meillä on vain vortiittisuus z-suunnassa. Tästä voimme nähdä, miten kukin neljästä eri termistä voi muuttaa vortiittisuutta.

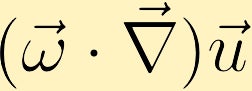
Jos tapahtuu nopeuden muutos olemassa olevan vortiittisuuden suuntaan, vortiittisuus voi syntyä.

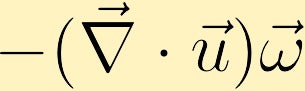
Jos fluidipaketti laajenee ja vortiittisuus on positiivinen, fluidipaketin vortiittisuus vähenee ja jos paketti supistuu, vortiittisuus lisääntyy.

Nestekerrokset, joiden tiheys on vakio (isopyknaalit), haluavat yhtyä vakiopainekerroksiin (isobaarit). Jos nämä kerrokset eivät ole yhtäpitäviä, fluidi alkaa pyöriä, jotta ne asettuisivat riviin, mikä aiheuttaa pyörteisyyttä. (Esimerkissä aloitamme nollalla vortiittisuudella.)

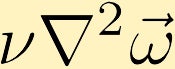
viskoosit voimat aiheuttavat pyörteisyyden diffuusion. (Esimerkissä aloitamme äärettömän vortiittisuuden pisteestä keskipisteessä.)