Toutes les techniques de régression contiennent une seule variable de sortie (réponse) et une ou plusieurs variables d’entrée (prédicteur). La variable de sortie est numérique. La méthodologie de construction d’arbres de régression générale permet aux variables d’entrée d’être un mélange de variables continues et catégorielles. Un arbre de décision est généré lorsque chaque nœud de décision de l’arbre contient un test sur la valeur d’une variable d’entrée. Les nœuds terminaux de l’arborescence contiennent les valeurs de variables de sortie prédites.

Un arbre de régression peut être considéré comme une variante des arbres de décision, conçus pour approximer des fonctions à valeurs réelles, au lieu d’être utilisés pour des méthodes de classification.

Méthodologie

Un arbre de régression est construit par un processus connu sous le nom de partitionnement récursif binaire, qui est un processus itératif qui divise les données en partitions ou branches, puis continue de diviser chaque partition en groupes plus petits à mesure que la méthode remonte chaque branche.

Initialement, tous les enregistrements de l’ensemble d’entraînement (enregistrements pré-classifiés utilisés pour déterminer la structure de l’arbre) sont regroupés dans la même partition. L’algorithme commence alors à allouer les données dans les deux premières partitions ou branches, en utilisant toutes les divisions binaires possibles sur chaque champ. L’algorithme sélectionne la division qui minimise la somme des écarts au carré par rapport à la moyenne dans les deux partitions séparées. Cette règle de division est ensuite appliquée à chacune des nouvelles branches. Ce processus se poursuit jusqu’à ce que chaque nœud atteigne une taille de nœud minimale spécifiée par l’utilisateur et devienne un nœud terminal. (Si la somme des écarts au carré par rapport à la moyenne dans un nœud est nulle, alors ce nœud est considéré comme un nœud terminal même s’il n’a pas atteint la taille minimale.)

Élagage de l’arbre

Comme l’arbre provient de l’Ensemble d’entraînement, un arbre complètement développé souffre généralement d’un ajustement excessif (c’est-à-dire qu’il explique des éléments aléatoires de l’Ensemble d’entraînement qui ne sont pas susceptibles d’être des caractéristiques de la population plus importante). Ce surajustement entraîne de mauvaises performances sur les données réelles. Par conséquent, l’arbre doit être élagué à l’aide de l’ensemble de validation. XLMiner calcule le facteur de complexité des coûts à chaque étape de la croissance de l’arbre et décide du nombre de nœuds de décision dans l’arbre taillé. Le facteur de complexité des coûts est le facteur multiplicatif appliqué à la taille de l’arbre (mesuré par le nombre de nœuds terminaux).

L’arbre est élagué pour minimiser la somme de :1) la variance de la variable de sortie dans les données de validation, prise un nœud terminal à la fois ; et 2) le produit du facteur de complexité des coûts et du nombre de nœuds terminaux. Si le facteur de complexité des coûts est spécifié comme zéro, l’élagage consiste simplement à trouver l’arbre qui fonctionne le mieux sur les données de validation en termes de variance totale du nœud terminal. Des valeurs plus élevées du facteur de complexité des coûts entraînent des arbres plus petits. L’élagage est effectué sur la base du dernier entré, premier sorti, ce qui signifie que le dernier nœud cultivé est le premier à être éliminé.

Méthodes d’ensemble

XLMiner V2015 propose trois méthodes d’ensemble puissantes pour une utilisation avec des arbres de régression : ensachage (agrégation bootstrap), boosting et arbres aléatoires. L’algorithme de l’arbre de régression peut être utilisé pour trouver un modèle qui donne de bonnes prédictions pour les nouvelles données. Nous pouvons voir les statistiques et les matrices de confusion du prédicteur actuel pour voir si notre modèle correspond bien aux données; mais comment saurions-nous s’il existe un meilleur prédicteur qui n’attend que d’être trouvé? La réponse est que nous ne savons pas s’il existe un meilleur prédicteur. Cependant, les méthodes d’ensemble nous permettent de combiner plusieurs modèles d’arbres de régression faibles, qui, pris ensemble, forment un nouveau modèle d’arbre de régression précis et fort. Ces méthodes fonctionnent en créant plusieurs modèles de régression divers, en prélevant différents échantillons de l’ensemble de données d’origine, puis en combinant leurs résultats. (Les résultats peuvent être combinés par plusieurs techniques, par exemple, le vote majoritaire pour la classification et la moyenne pour la régression) Cette combinaison de modèles réduit efficacement la variance dans le modèle fort. Les trois types de méthodes d’ensemble proposées dans XLMiner (ensachage, amplification et arbres aléatoires) diffèrent sur trois éléments: 1) la sélection de l’ensemble d’entraînement pour chaque prédicteur ou modèle faible; 2) comment les modèles faibles sont générés; et 3) comment les sorties sont combinées. Dans les trois méthodes, chaque modèle faible est formé sur l’ensemble de l’ensemble de formation pour devenir compétent dans une partie de l’ensemble de données.

L’ensachage (bootstrap aggregating) a été l’un des premiers algorithmes d’ensemble jamais écrits. C’est un algorithme simple, mais très efficace. L’ensachage génère plusieurs ensembles d’entraînement en utilisant un échantillonnage aléatoire avec remplacement (échantillonnage bootstrap), applique l’algorithme de l’arbre de régression à chaque ensemble de données, puis prend la moyenne parmi les modèles pour calculer les prédictions pour les nouvelles données. Le plus grand avantage de l’ensachage est la facilité relative de parallélisation de l’algorithme, ce qui en fait une meilleure sélection pour de très grands ensembles de données.

Boosting construit un modèle solide en entraînant successivement des modèles pour se concentrer sur les enregistrements recevant des valeurs prédites inexactes dans les modèles précédents. Une fois terminé, tous les prédicteurs sont combinés par un vote majoritaire pondéré. XLMiner propose trois variantes de boosting implémentées par l’algorithme AdaBoost (l’un des algorithmes d’ensemble les plus populaires utilisés aujourd’hui): M1 (Freund), M1 (Breiman) et SAMME (Modélisation additive par étapes utilisant une Exponentielle Multi-classes).

Adaboost.M1 attribue d’abord une pondération (wb(i)) à chaque enregistrement ou observation. Ce poids est initialement fixé à 1/n, et sera mis à jour à chaque itération de l’algorithme. Un arbre de régression original est créé à l’aide de ce premier ensemble d’entraînement (Tb) et une erreur est calculée comme

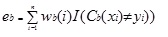
où, la fonction I() renvoie 1 si true et 0 si non.

L’erreur de l’arbre de régression dans la bème itération est utilisée pour calculer la constante ?b. Cette constante est utilisée pour mettre à jour le poids (wb(i). À AdaBoost.M1(Freund), la constante est calculée comme

ab= ln((1-eb)/eb)

Dans AdaBoost.M1(Breiman), la constante est calculée comme

ab = 1 / 2ln((1-eb)/eb)

Dans SAMME, la constante est calculée comme

ab = 1/2ln((1-eb)/eb +ln(k-1) où k est le nombre de classes

où, le nombre de catégories est égal à 2, SAMME se comporte de la même manière qu’AdaBoost Breiman.

Dans l’une des trois implémentations (Freund, Breiman ou SAMME), le nouveau poids pour la (b+1)th itération sera

Ensuite, les poids sont tous réajustés à la somme de 1. En conséquence, les poids attribués aux observations auxquelles des valeurs prédites inexactes ont été attribuées sont augmentés et les poids attribués aux observations auxquelles des valeurs prédites précises ont été attribuées sont diminués. Cet ajustement force le modèle de régression suivant à mettre davantage l’accent sur les enregistrements auxquels des prédictions inexactes ont été attribuées. (Ceci? la constante est également utilisée dans le calcul final, ce qui donnera plus d’influence au modèle de régression avec l’erreur la plus faible.) Ce processus se répète jusqu’à b = Nombre d’apprenants faibles. L’algorithme calcule ensuite la moyenne pondérée parmi tous les apprenants faibles et attribue cette valeur à l’enregistrement. L’amplification donne généralement de meilleurs modèles que l’ensachage; cependant, elle présente un inconvénient car elle n’est pas parallélisable. Par conséquent, si le nombre d’apprenants faibles est important, le renforcement ne conviendrait pas.

La méthode des arbres aléatoires (forêts aléatoires) est une variante de l’ensachage. Cette méthode fonctionne en entraînant plusieurs arbres de régression faibles en utilisant un nombre fixe d’entités sélectionnées au hasard (sqrt pour la classification et le nombre d’entités / 3 pour la prédiction), puis prend la valeur moyenne pour les apprenants faibles et attribue cette valeur au prédicteur fort. Typiquement, le nombre d’arbres faibles générés peut varier de plusieurs centaines à plusieurs milliers selon la taille et la difficulté de l’ensemble d’entraînement. Les arbres aléatoires sont parallélisables, car ils sont une variante de l’ensachage. Cependant, comme les arbres tandom sélectionnent un nombre limité de fonctionnalités à chaque itération, les performances des arbres aléatoires sont plus rapides que l’ensachage.

Les méthodes d’ensemble d’arbres de régression sont des méthodes très puissantes, et entraînent généralement de meilleures performances qu’un seul arbre. Cet ajout de fonctionnalité dans XLMiner V2015 fournit des modèles de prédiction plus précis et doit être pris en compte sur la méthode de l’arbre unique.