Dans certaines circonstances, le courant dans l’enroulement d’un inducteur toroïdal ne contribue qu’au champ B à l’intérieur des enroulements et ne contribue pas au champ magnétique B à l’extérieur des enroulements. Ceci est une conséquence de la symétrie et de la loi circuitale d’Ampère.

Conditions suffisantes pour le confinement interne total du champ B

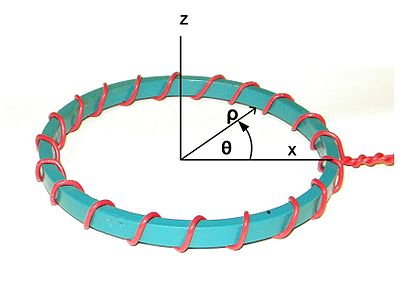Fig. 1. Système de coordonnées. L’axe Z est l’axe de symétrie nominal. L’axe des abscisses choisi arbitrairement pour s’aligner avec le point de départ de l’enroulement. ρ est appelée la direction radiale. θ est appelée direction circonférentielle.

Fig. 2. Un inducteur toroïdal à symétrie axiale sans courant circonférentiel.

L’absence de courant circonférentiel (le trajet du courant circonférentiel est indiqué par la flèche rouge sur la figure 3 de cette section) et la disposition axialement symétrique des conducteurs et des matériaux magnétiques sont des conditions suffisantes pour un confinement interne total du champ B. (Certains auteurs préfèrent utiliser le champ H). Du fait de la symétrie, les lignes de flux B doivent former des cercles d’intensité constante centrés sur l’axe de symétrie. Les seules lignes de flux B qui encerclent un courant sont celles qui se trouvent à l’intérieur de l’enroulement toroïdal. Par conséquent, d’après la loi de circuit d’Ampère, l’intensité du champ B doit être nulle en dehors des enroulements.

Fig. 3. Inducteur toroïdal à courant circonférentiel

La figure 3 de cette section montre l’enroulement toroïdal le plus courant. Il ne satisfait pas aux deux exigences pour le confinement total sur le terrain B. En regardant de l’axe, parfois l’enroulement est à l’intérieur du noyau et parfois à l’extérieur du noyau. Il n’est pas symétrique axialement dans la région proche. Cependant, à des points distants de plusieurs fois l’espacement de l’enroulement, le tore semble symétrique. Il reste le problème du courant circonférentiel. Peu importe combien de fois l’enroulement entoure le noyau et quelle que soit la finesse du fil, cet inducteur toroïdal comprendra toujours une boucle à une bobine dans le plan du tore. Cet enroulement va également produire et être sensible à un champ E dans le plan de l’inducteur.

Les figures 4 à 6 montrent différentes façons de neutraliser le courant circonférentiel. La figure 4 est la plus simple et présente l’avantage que le fil de retour peut être ajouté après l’achat ou la construction de l’inducteur.

Fig. 4. Courant circonférentiel contré par un fil de retour. Le fil est blanc et passe entre le bord extérieur de l’inducteur et la partie extérieure de l’enroulement.

Fig. 5. Courant circonférentiel contré par un enroulement de retour.

Fig. 6. Courant circonférentiel contré par un enroulement de retour fendu.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

Il y aura une distribution du potentiel le long de l’enroulement. Cela peut conduire à un champ E dans le plan du tore et également à une susceptibilité à un champ E dans le plan du tore comme le montre la figure 7. Cela peut être atténué en utilisant un enroulement de retour comme indiqué sur la figure 8. Avec cet enroulement, à chaque endroit que l’enroulement se croise, les deux parties seront à polarité égale et opposée ce qui réduit sensiblement le champ E généré dans le plan.

Inducteur / transformateur toroïdal et potentiel vectoriel magnétiquEdit

Montrant le développement du potentiel vectoriel magnétique autour d’un inducteur toroïdal symétrique.

Voir les chapitres 14 et 15 de Feynman pour une discussion générale sur le potentiel de vecteur magnétique. Voir page 15-11 de Feynman pour un diagramme du potentiel de vecteur magnétique autour d’un solénoïde long et mince qui présente également un confinement interne total du champ B, au moins dans la limite infinie.

Le champ A est précis lorsque l’on utilise l’hypothèse b f A = 0 {\displaystyle bf {A}=0}

. Cela serait vrai sous les hypothèses suivantes:

• 1. la jauge de Coulomb est utilisée
• 2. la jauge de Lorenz est utilisée et il n’y a pas de distribution de charge, ρ = 0 {\displaystyle\rho= 0\,}
  
• 3. la jauge de Lorenz est utilisée et la fréquence zéro est supposée
• 4. la jauge de Lorenz est utilisée et une fréquence non nulle suffisamment faible pour négliger 1 c 2 tt {\displaystyle {\frac{1}{c^{2}}}{\frac{\partial\phi}{\partial t}}}
  

  est supposée.

Le numéro 4 sera présumé pour le reste de cette section et peut être référé à la « condition quasi statique ».

Bien que l’inducteur toroïdal à symétrie axiale sans courant circonférentiel confine totalement le champ B à l’intérieur des enroulements, le champ A (potentiel vectoriel magnétique) n’est pas confiné. La flèche #1 de l’image représente le potentiel vectoriel sur l’axe de symétrie. Les sections de courant radial a et b sont à égale distance de l’axe mais pointées dans des directions opposées, elles s’annuleront donc. De même, les segments c et d s’annulent. En effet, tous les segments de courant radial s’annulent. La situation pour les courants axiaux est différente. Le courant axial à l’extérieur du tore est pointé vers le bas et le courant axial à l’intérieur du tore est pointé vers le haut. Chaque segment de courant axial à l’extérieur du tore peut être mis en correspondance avec un segment de direction égale mais opposée à l’intérieur du tore. Les segments à l’intérieur sont plus proches que les segments à l’extérieur de l’axe, il y a donc une composante ascendante nette du champ A le long de l’axe de symétrie.

Représentant les champs de potentiel de vecteur magnétique (A), de flux magnétique (B) et de densité de courant (j) autour d’un inducteur toroïdal de section circulaire. Des lignes plus épaisses indiquent des lignes de champ d’intensité moyenne plus élevée. Les cercles en coupe transversale du noyau représentent le flux B sortant de l’image. Les signes Plus sur l’autre section transversale du noyau représentent le flux B entrant dans l’image. Div A = 0 a été supposé.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂E tt → 0 {\displaystyle {\frac {\partial E} {\partial t}} \rightarrow 0}

) ont la même forme, alors les lignes et les contours de A se rapportent à B comme les lignes et les contours de B se rapportent à j. Ainsi, une représentation du champ A autour d’une boucle de flux B ( comme on le ferait dans un inducteur toroïdal) est qualitativement le même que le champ B autour d’une boucle de courant. La figure à gauche est une représentation d’artiste du champ A autour d’un inducteur toroïdal. Les lignes plus épaisses indiquent des chemins d’intensité moyenne plus élevée (les chemins plus courts ont une intensité plus élevée, de sorte que l’intégrale du chemin est la même). Les lignes sont juste dessinées pour bien paraître et donner un aspect général du champ A.

Action du transformateur toroïdal en présence du confinement total du champ B

Les champs E et B peuvent être calculés à partir des champs A et {{\displaystyle\phi\,}

(potentiel électrique scalaire) B = ××A. {\displaystyle\mathbf{B} = \nabla\times\mathbf{A}.}

et : E =−displ− A A tt {\displaystyle\mathbf{E}= -\nabla\phi-{\frac{\partial\mathbf{A}}{\partial t}}}

et donc même si la région en dehors des enroulements est dépourvue de champ B, elle est remplie de champ E non nul. La quantité AA tt {\displaystyle{\frac{\partial\mathbf{A}}{\partial t}}}

est responsable du couplage de champ magnétique souhaitable entre primaire et secondaire tandis que la quantité ∇ ϕ{\displaystyle\nabla\phi\,}

est responsable du couplage de champ électrique indésirable entre primaire et secondaire. Les concepteurs de transformateurs tentent de minimiser le couplage du champ électrique. Pour le reste de cette section, ∇ ϕ{\displaystyle\nabla\phi\,}

sera supposé être nul, sauf indication contraire.

Le théorème de Stokes s’applique, de sorte que l’intégrale de chemin de A est égale au flux B fermé, tout comme l’intégrale de chemin B est égale à une constante fois le courant fermé

L’intégrale de chemin de E le long de l’enroulement secondaire donne la force électromagnétique induite du secondaire (Force électro-motrice).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

qui indique que la FEM est égale à la vitesse temporelle de changement du flux B enfermé par l’enroulement, ce qui est le résultat habituel.

Couplage vectoriel de Poynting de transformateur toroïdal du primaire au secondaire en présence d’un confinement total du champ B

Dans ce figure, les points bleus indiquent où le flux B du courant primaire sort de l’image et les signes plus indiquent où il entre dans l’image.

Explication de la figuredit

Cette figure montre la demi-section d’un transformateur toroïdal. Les conditions quasi statiques sont supposées, de sorte que la phase de chaque champ est partout la même. Le transformateur, ses enroulements et toutes choses sont répartis symétriquement autour de l’axe de symétrie. Les enroulements sont tels qu’il n’y a pas de courant circonférentiel. Les exigences sont remplies pour le confinement interne complet du champ B en raison du courant primaire. Le noyau et l’enroulement primaire sont représentés par le tore gris-brun. L’enroulement primaire n’est pas représenté, mais le courant dans l’enroulement à la surface de la section transversale est représenté sous forme d’ellipses dorées (ou orange). Le champ B provoqué par le courant primaire est entièrement confiné à la région enfermée par l’enroulement primaire (c’est-à-dire le noyau). Des points bleus sur la section transversale de la main gauche indiquent que des lignes de flux B dans le noyau sortent de la section transversale de la main gauche. Sur l’autre section transversale, des signes plus bleus indiquent que le flux B y pénètre. Le champ E provenant des courants primaires est représenté sous forme d’ellipses vertes. L’enroulement secondaire est représenté sous la forme d’une ligne brune descendant directement sur l’axe de symétrie. En pratique normale, les deux extrémités du secondaire sont reliées entre elles par un long fil qui reste bien éloigné du tore, mais pour maintenir la symétrie axiale absolue, l’ensemble de l’appareil est envisagé comme étant à l’intérieur d’une sphère parfaitement conductrice avec le fil secondaire « mis à la terre » à l’intérieur de la sphère à chaque extrémité. Le secondaire est fait de fil de résistance, il n’y a donc pas de charge séparée. Le champ E le long du secondaire provoque un courant dans le secondaire (flèches jaunes) qui provoque un champ B autour du secondaire (représenté par des ellipses bleues). Ce champ B remplit l’espace, y compris à l’intérieur du noyau du transformateur, de sorte qu’à la fin, il y a un champ B continu non nul du primaire au secondaire, si le secondaire n’est pas en circuit ouvert. Le produit croisé du champ E (provenant des courants primaires) et du champ B (provenant des courants secondaires) forme le vecteur de Poynting qui pointe du primaire vers le secondaire.