Introduction

effectieve populatiegrootte (Ne) is een belangrijke genetische parameter die de hoeveelheid genetische drift in een populatie schat, en is beschreven als de grootte van een geïdealiseerde Wright–Fisher-populatie die naar verwachting dezelfde waarde van een bepaalde genetische parameter zal opleveren als in de bestudeerde populatie (Crow en Kimura, 1970). Ne maten kunnen worden beïnvloed door schommelingen in de census population size (Nc), door de geslachtsverhouding van de voortplanting en de variantie in reproductief succes.

ne schatting kan worden bereikt met benaderingen die vallen in drie methodologische categorieën: demografisch, stamboom-gebaseerd, of marker-gebaseerd (Flury et al., 2010). Van oudsher worden stamboomgegevens gebruikt om Ne-schattingen voor vee te verkrijgen. Betrouwbare schattingen van Ne hangen echter af van de volledige stamboom. Deze stand van kennis is haalbaar in sommige huishoudens, waarvan de demografische parameters nauwkeurig zijn gecontroleerd voor een voldoende groot aantal generaties. In de praktijk blijft de toepasbaarheid van deze aanpak echter beperkt tot enkele gevallen waarbij sterk beheerde rassen betrokken zijn (Flury et al., 2010; Uimari en Tapio, 2011).

een oplossing om de beperking van een onvolledige stamboom te overwinnen is het schatten van de recente trend in Ne met behulp van genomische gegevens. Verschillende auteurs hebben erkend dat Ne kan worden geschat aan de hand van informatie over het gebrek aan evenwicht in de koppeling (LD) (Sved, 1971; Hill, 1981). LD beschrijft de niet-willekeurige Vereniging van allelen in verschillende loci als functie van het recombinatietarief tussen de fysische posities van loci in het genoom. Echter, LD handtekeningen kunnen ook het gevolg zijn van demografische processen zoals vermenging en genetische drift (Wright, 1943; Wang, 2005), of door processen zoals “liften” tijdens selectieve sweeps (Smith en Haigh, 1974) of achtergrond selectie (Charlesworth et al., 1997). In dergelijke scenario ‘ s worden allelen bij verschillende plaatsen onafhankelijk van hun nabijheid in het genoom geassocieerd. Aangenomen dat een populatie gesloten en panmictisch is, hangt de LD-waarde berekend tussen neutrale niet-verbonden loci uitsluitend af van genetische drift (Sved, 1971; Hill, 1981). Dit voorkomen kan worden gebruikt om Ne te voorspellen vanwege het bekende verband tussen de variantie in LD (berekend aan de hand van allelfrequenties) en de effectieve populatiegrootte (Hill, 1981).

recente ontwikkelingen in genotyperingstechnologie (bijv., met behulp van SNP parel arrays met tienduizenden DNA-sondes) hebben de verzameling van enorme hoeveelheden genoom-brede koppeling gegevens ideaal voor het schatten van Ne in vee en mensen onder anderen (bijv., tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2010; Uimari and Tapio, 2011; Kijas et al., 2012). Echter, een software tool die het mogelijk maakt schatting van Ne van LD ontbreekt, en onderzoekers vertrouwen momenteel op een combinatie van tools om gegevens te manipuleren, af te leiden LD, en de neiging om op maat gemaakte scripts gebruiken om de juiste berekeningen uit te voeren en schatting Ne.

Hier beschrijven we SNeP, een software tool die het mogelijk maakt de schatting van Ne trends over generatie met behulp van SNP data die corrigeert voor steekproefgrootte, phasing en recombinatie snelheid.

materialen en methoden

De methode die SNeP gebruikt om LD te berekenen, hangt af van de beschikbaarheid van gefaseerde gegevens. Wanneer de fase bekend is kan de gebruiker Hill en Robertson (1968) kwadraat correlatiecoëfficiënt selecteren die gebruik maakt van haplotypefrequenties om LD te definiëren tussen elk paar loci (vergelijking 1). Echter, bij afwezigheid van een bekende fase, squared Pearson ‘ s product-moment correlatiecoëfficiënt tussen paren van loci kan worden geselecteerd. Hoewel deze twee benaderingen niet hetzelfde zijn, zijn ze zeer vergelijkbaar (McEvoy et al., 2011):

waar pA en pB zijn respectievelijk de frequenties van de allelen A en B op twee afzonderlijke loci (X, Y) gemeten voor n individuen, pAB is de frequentie van het haplotype met de allelen A en B in de bestudeerde populatie, X en Y het gemiddelde van de genotype frequenties voor de eerste en tweede plaats, respectievelijk, Xi is het genotype van individu i op de eerste plaats en Yi is het genotype van individu i op de tweede plaats. Vergelijking (2) correleert de genotypische alleltellingen in plaats van de haplotypefrequenties en wordt niet beïnvloed door dubbele heterozygotes (deze benadering resulteert in dezelfde schattingen als de –r2 optie in PLINK).

SNeP schat de historische effectieve populatiegrootte op basis van het verband tussen r2, Ne en c (recombinatiesnelheid), (vergelijking 3—Sved, 1971), en stelt gebruikers in staat correcties op te nemen voor steekproefgrootte en onzekerheid van de gametische fase (vergelijking 4-Weir en Hill, 1980):

radj2=r2−(ßn)-1 (4)

waarbij n het aantal individuele monsters is, β = 2 Wanneer de gametische fase bekend is en β = 1 indien de fase niet bekend is.

verschillende benaderingen worden gebruikt om de recombinatiesnelheid af te leiden met behulp van de fysieke afstand (δ) tussen twee loci als referentie en deze om te zetten in koppelingsafstand (d), die gewoonlijk wordt beschreven als Mb(δ) ≈ cM(d). Voor kleine waarden van d is deze laatste benadering geldig, maar voor grotere waarden van d neemt de kans op meervoudige recombinatiegebeurtenissen en interferentie toe, bovendien is de relatie tussen kaartafstand en recombinatiesnelheid niet lineair, aangezien de maximale recombinatiesnelheid mogelijk 0,5 is. Dus, tenzij het gebruik van zeer korte δ, de benadering d ≈ c is niet ideaal (Corbin et al., 2012). Daarom implementeerden we mapping functies om de geschatte d te vertalen naar c, volgend op Haldane (1919), Kosambi (1943), Sved (1971), en Sved and Feldman (1973). Aanvankelijk leidt SNeP D voor elk paar SNP ‘ s af als recht evenredig met δ volgens d = kδ waarbij k een door de gebruiker gedefinieerde recombinatiesnelheid is (standaardwaarde is 10-8 zoals in Mb = cM). De afgeleide waarde δ kan dan worden onderworpen aan een van de beschikbare mapping functies indien vereist door de gebruiker.

Oplossingsvergelijking (3) voor Ne en met inbegrip van alle beschreven correcties, maakt de voorspelling van Ne uit LD-gegevens met behulp van (Corbin et al., 2012):

NT (t) = (4f(ct)) -1(E −1−α) (5)

waarbij Nt de effectieve populatiegrootte t generaties geleden is, berekend als t = (2f(ct)) -1 (Hayes et al., 2003), ct is de recombinatiesnelheid gedefinieerd voor een specifieke fysieke afstand tussen markers en optioneel aangepast met de mapping functies hierboven vermeld, r2adj is de LD-waarde aangepast voor steekproefgrootte en α:= {1, 2, 2.2} is een correctie voor het voorkomen van mutaties (Ohta en Kimura, 1971). Daarom is LD over Grotere recombinante afstanden informatief over recente Ne, terwijl kortere afstanden informatie verschaffen over verder verwijderde tijden in het verleden. Er wordt een binningssysteem geïmplementeerd om gemiddelde r2-waarden te verkrijgen die LD weergeven voor specifieke interlokale afstanden. Het ingevoerde binning-systeem gebruikt de volgende formule om de minimum-en maximumwaarden voor elke bin te definiëren:

bimin=geest+(maxD−minD) (bi−1totBins)x (6a)

bimax=geest+(maxD−minD) (bitotBins)x (6b)

Waar bi (ℕ1) is de i-de bin van het totale aantal bakken (totBins), de geest, en maxD zijn respectievelijk de minimum en de maximum afstand tussen SNPs en x is een positief reëel getal (ℝ0) Wanneer x gelijk is aan 1, is de verdeling van de afstanden tussen de bakken is lineair en elke bak heeft dezelfde afstand. Voor grotere waarden van x verandert de verdeling van afstanden waardoor een groter bereik op de laatste bakken en een kleiner bereik op de eerste bakken. Door deze parameter te variëren kan de gebruiker een voldoende aantal paarsgewijze vergelijkingen hebben om bij te dragen aan de uiteindelijke ne schatting voor elke bin.

voorbeeldtoepassing

We hebben SNeP Getest met twee gepubliceerde datasets die eerder waren gebruikt om trends in Ne in de loop van de tijd te beschrijven met behulp van LD, Bos indicus en Ovis aries . De R2 schattingen voor de vee datasets werden verkregen door de auteurs met behulp van GenABLE (Aulchenko et al., 2007) met behulp van een minimum allelfrequentie (MAF) < 0,01 en de recombinatiesnelheid aanpassen met behulp van de mapping-functie van Haldane (Haldane, 1919). De R2 schattingen van de schapen gegevens werden berekend door de auteurs met behulp van PLINK-1.07 (Purcell et al., 2007), met een MAF < 0,05 en geen verdere correcties. Voor beide autosomale datasets zijn R2-schattingen gecorrigeerd voor steekproefgrootte met behulp van vergelijking (4) Met β = 2. Voor deze vergelijkende analyses bevatte de SNeP-opdrachtregel dezelfde parameters die voor de gepubliceerde gegevens werden gebruikt, afgezien van de R2-schattingen, berekend aan de hand van genotype-telling en het gebruik van SNeP ‘ s nieuwe binning-strategie.

Results

SNeP is een multithreaded applicatie ontwikkeld in C++ en binaries voor de meest voorkomende besturingssystemen (Windows, OSX en Linux) kan worden gedownload vanhttps://sourceforge.net/projects/snepnetrends/. De binaries gaan vergezeld van een handleiding die het stap-voor-stap gebruik van SNeP beschrijft om trends in Ne af te leiden zoals hier beschreven. SNeP produceert een uitvoerbestand met tab gescheiden kolommen die het volgende tonen voor elke bin die werd gebruikt om Ne te schatten: het aantal generaties in het verleden dat de bin overeenkomt met (bijv., 50 generaties geleden), de overeenkomstige ne schatting, de gemiddelde afstand tussen elk paar SNP ’s in de bak, de gemiddelde r2 en de standaardafwijking van r2 in de bak, en het aantal SNP’ s gebruikt om r2 in de bak te berekenen. Dit bestand kan eenvoudig worden geïmporteerd in Microsoft Excel, R of andere software om de resultaten te plotten. De hier getoonde plots (figuren 1, 3) komen overeen met de kolommen van generaties geleden en Ne uit het uitvoerbestand. De kolom met de standaardafwijking r2 wordt verstrekt zodat gebruikers de variantie in de ne-schatting in elke bak kunnen inspecteren, met name voor die bakken die oudere tijdschattingen weergeven en die minder betrouwbaar zijn naarmate het aantal SNP ‘ s dat wordt gebruikt om r2 te schatten kleiner wordt.

figuur 1

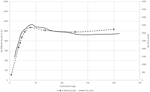
figuur 1. Vergelijking van Ne trends van zes Zwitserse schapenrassen volgens Burren et al. (2014) (gestippelde lijnen) en dit werk (vaste lijnen).

het vereiste formaat voor de invoerbestanden is het standaard PLINK formaat (ped en map bestanden) (Purcell et al., 2007). SNeP stelt de gebruikers in staat om LD te berekenen op de gegevens zoals hierboven beschreven, of een aangepaste vooraf berekende LD-matrix te gebruiken om Ne te schatten met behulp van vergelijking (5).

de software-interface stelt de gebruiker in staat om alle parameters van de analyse te controleren, bijvoorbeeld de afstand tussen SNP ‘ s in bp, en de reeks chromosomen die bij de analyse worden gebruikt (bijvoorbeeld 20-23). Daarnaast bevat SNeP de optie om een maf drempel te kiezen (standaard 0.05), aangezien is aangetoond dat de boekhouding van MAF resulteert in onbevooroordeelde R2-ramingen, ongeacht de omvang van de steekproef (Sved et al., 2008). SNeP ’s multithreaded architectuur maakt snelle berekening van grote datasets (we getest tot ~100K SNPs voor een enkele chromosoom), bijvoorbeeld de BOS-gegevens hier beschreven werd geanalyseerd met een processor in 2’43”, het gebruik van twee processors verminderde de tijd tot 1’43”, vier processors verminderde de analysetijd tot 1’05”.

Zebu voorbeeld

voor de Zebu-analyse lieten de vormen van de ne-krommen die met SNeP werden verkregen en hun gepubliceerde gegevenstrends hetzelfde traject zien met een soepele afname tot ongeveer 150 generaties geleden, gevolgd door een expansie met een piek van ongeveer 40 generaties geleden en eindigend in een sterke afname ten opzichte van de meest recente generaties (figuur 1). Hoewel de trends in beide curven hetzelfde waren, resulteerden de twee benaderingen in verschillende ne-schattingen, waarbij de SNeP-waarden ongeveer drie keer groter waren dan die in het oorspronkelijke document. Terwijl we probeerden de parameters van de auteurs te gebruiken in onze analyses, waren enkele verschillen onvermijdelijk, dat wil zeggen, de oorspronkelijke publicatie van de R2-gegevens voor runderen met een andere aanpak dan die in SNeP. Analyses met SNeP waren gebaseerd op genotypes, terwijl de oorspronkelijke analyse gebaseerd was op twee Locus haplotypes, wat resulteert in de gepubliceerde gegevens die een verwachte r2 van 0,32 op de minimale afstand tonen, terwijl onze schattingen 0,23 waren. Evenzo, Mbole-Kariuki et al. (2014) behaalde een achtergrondniveau r2 = 0,013 rond 2 Mb, terwijl onze schatting op dezelfde afstand 0 was.0035 (gegevens niet weergegeven). Bijgevolg, als onze schattingen van LD waren consequent kleiner dan Mbole-Kariuki et al. (2014) de verwachting is dat onze ne schattingen groter moeten zijn. Hoewel deze observatie het belang onderstreept van een zorgvuldige keuze van de parameters en hun drempels, is het belangrijk te benadrukken dat, hoewel de absolute grootte van de Ne-waarden verschillend is, de trends vrijwel identiek zijn.

Swiss Sheep voorbeeld

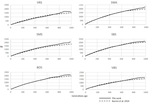
de zes Zwitserse schapenrassen geanalyseerd met SNeP leverde vergelijkbare resultaten op met die van het oorspronkelijke papier (figuur 2), Met meestal overlappende ne trendcurves (Figuur 3). De algemene trend in Ne vertoonde echter een daling in de richting van het heden. SNeP produceerde iets grotere waarden van Ne voor het verre verleden (700-800 generaties). Dit is te wijten aan het verschillende binning systeem gebruikt in SNeP, die de gebruiker in staat stelt om een meer gelijkmatige verdeling van paarsgewijze vergelijkingen binnen elke bin (d.w.z., het aantal SNP paarsgewijze vergelijkingen binnen elke bin is vergelijkbaar). Voor de tijdspanne die verder gaat dan 400 generaties geleden, Burren et al. (2014) gebruikt slechts drie bakken in hun analyse (gecentreerd op 400, 667, en 2000 generaties geleden) terwijl voor dezelfde tijdsspanne SNeP gebruikt 5 bakken met een aantal paarsgewijze vergelijkingen afhankelijk van het bereik gedefinieerd met formules 6a,b. bijgevolg, Burren en collega’ s aanpak eindigt met een hogere dichtheid van gegevens beschrijven van de meest recente generaties dan het beschrijven van de oudste generaties. Daarom heeft het gebruik van minder bakken de neiging om de aanwezigheid van kleinere waarden van Ne in elke bak te verhogen, waardoor de gemiddelde waarde van Ne voor elke bak daalt. De Ne-waarden voor het recente verleden, vergeleken bij de 29e generatie in het verleden, gaven zeer vergelijkbare resultaten. Het grootste verschil (50) werd verkregen voor het SBS ras.

figuur 2

Figuur 2. Vergelijking tussen recente Ne-waarden berekend bij de 29e generatie in dit werk en Burren et al. (2014) voor zes Zwitserse schapenrassen.

figuur 3

Figuur 3. Vergelijking van Ne trends voor de laatste 250 generaties in de SHZ gegevens verkregen door Mbole-Kariuki et al. (2014) (stippellijn) en het gebruik van SNeP (vaste lijn).

discussie

analyse van Ne met behulp van LD-gegevens werd 40 jaar geleden voor het eerst aangetoond en is sindsdien toegepast, ontwikkeld en verbeterd (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Het traditioneel kleine aantal SNP ’s geanalyseerd is niet langer een beperking, omdat SNP-Chips bestaan uit een extreem groot aantal SNP’ s, beschikbaar in een korte tijd en tegen een redelijke prijs. Dit heeft het gebruik van de methode, die is toegepast op de mens gestimuleerd (Tenesa et al., 2007; McEvoy et al., 2011) en op verschillende gedomesticeerde soorten (England et al., 2006; Uimari and Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Naast deze verbeteringen zijn methodologische beperkingen aan het licht gekomen en hier aan de orde gesteld, waarbij het merendeel van de inspanningen wijst op de juiste schatting van recente Ne. Toch is de kwantitatieve waarde van de schatting sterk afhankelijk van de steekproefgrootte, het type LD-schatting en het binningproces (Waples and Do, 2008; Corbin et al., 2012), terwijl het kwalitatieve patroon meer afhangt van de genetische informatie dan van datamanipulatie.

tot nu toe werd deze methode toegepast met behulp van een verscheidenheid aan software, Er bestaat geen gestandaardiseerde benadering om de resultaten te bineren en elke studie heeft een min of meer willekeurige benadering toegepast, bijvoorbeeld binning voor generatieklassen in het verleden (Corbin et al., 2012), binning voor afstandklassen met een constant bereik voor elke bin (Kijas et al., 2012) of binning per afstand klassen op een lineaire manier, maar met grotere bakken voor de meer recente tijdpunten (Burren et al., 2014). Voor zover wij weten is de enige beschikbare software die Ne schatten via LD NeEstimator (Do et al., 2014), een verbeterde versie van de voormalige LDNE (Waples and Do, 2008) waardoor de analyse van grote dataset (als 50k SNPChip). Belangrijk is dat, terwijl SNeP zich richt op het schatten van historische Ne-trends, NeEstimator ‘ s doel is om hedendaagse onbevooroordeelde Ne-schattingen te produceren, de laatste daarom moet worden beschouwd als een complementair instrument bij het onderzoeken van Demografie door middel van LD.

We gebruikten SNeP om twee datasets te analyseren waar de methode eerder werd toegepast. De resultaten die we verkregen voor de schapen gegevens waren zowel kwantitatief als kwalitatief vergelijkbaar met die verkregen door Burren et al. (2014), terwijl voor de Zebu gegevens verkregen we een Ne trend schatting die nauw overeenkomt met die van Mbole-Kariuki et al. (2014) hoewel onze puntschattingen van Ne waren groter dan die beschreven voor de gegevens (Mbole-Kariuki et al., 2014). De discrepantie tussen deze twee resultaten weerspiegelt dat Burren en collega ‘ s produceerde hun R2 schattingen met behulp van PLINK (de standaard software voor grootschalige SNP data manipulatie) die dezelfde benadering gebruikt om R2 schatten door SNeP gebruikt, terwijl Mbole-Kariuki et al. gevolgd door Hao et al. (2007) voor R2-schatting. Het gebruik van verschillende schattingen voor LD is van cruciaal belang voor het kwantitatieve aspect van de ne-curve, waar als gevolg van de hyperbolische correlatie tussen Ne en r2, een afname van r2 op zijn bereik dichter bij 0 kan leiden tot een zeer grote verandering in NE-schattingen, terwijl verschillen in schattingen minder significant zijn wanneer de r2-waarde hoog is, d.w.z. dichter bij 1. Hoewel in een van de datasets de Ne-waarden wezenlijk verschillend waren, overlapten de ne-curves in beide gevallen met de oorspronkelijk gepubliceerde curves.

zoals reeds door andere auteurs is gesuggereerd, moet de betrouwbaarheid van de met deze methode verkregen kwantitatieve schattingen met de nodige voorzichtigheid worden betracht, vooral voor Ne-waarden die betrekking hebben op de meest recente en de oudste generaties (Corbin et al., 2012) omdat voor recente generaties grote waarden van c betrokken zijn, niet passend bij de theoretische implicaties die Hayes voorstelde om een variabele Ne in de tijd te schatten (Hayes et al., 2003). Schattingen voor de oudste generaties kunnen ook onbetrouwbaar zijn als coalescentietheorie laat zien dat geen SNP betrouwbaar kan worden bemonsterd na 4Ne generaties in het verleden (Corbin et al., 2012). Verder worden ne-schattingen, en vooral die met betrekking tot generaties verder in het verleden, sterk beïnvloed door gegevensmanipulatiefactoren, zoals de keuze van MAF-en alfa-waarden. Bovendien kan de toegepaste binningstrategie de Algemene precisie van de methode verstoren, bijvoorbeeld wanneer er onvoldoende paarsgewijze vergelijkingen worden gebruikt om elke bin te vullen.

een van de toepassingen van de methode is het vergelijken van rasdemografieën. In dit geval zou de vorm van de ne-krommen het optimale instrument zijn om verschillende demografische geschiedenissen te onderscheiden, meer dan hun numerieke waarden, door ze te gebruiken als een potentiële demografische vingerafdruk voor dat ras of die soort, maar rekening houdend met het feit dat mutatie, migratie en selectie de ne-schatting kunnen beïnvloeden door middel van LD (Waples and Do, 2010). Bovendien, zorgvuldige overweging van de gegevens geanalyseerd met SNeP (en andere software om Ne te schatten) is zeer belangrijk, als de aanwezigheid van verstorende factoren zoals bijmenging, kan resulteren in bevooroordeelde schattingen van Ne (Orozco-terWengel and Bruford, 2014).

Het doel van SNeP is daarom een snel en betrouwbaar hulpmiddel te bieden om LD-methoden toe te passen om Ne te schatten met behulp van genotypische gegevens met een hoge doorvoer op een consistentere manier. Het maakt twee verschillende R2 schatting benaderingen plus de optie van het gebruik van R2 schattingen van externe software. Het gebruik van SNeP overwint niet de grenzen van de methode en de theorie erachter, maar het staat de gebruiker toe om de theorie toe te passen met behulp van alle correcties die tot op heden worden voorgesteld.

Auteursbijdragen

MB bedacht en schreef de software en het manuscript. MB, MT en POtW hebben de software getest en de analyses uitgevoerd. MT, POtW en MWB reviseerden het manuscript. Alle auteurs keurden het definitieve manuscript goed.

belangenconflict verklaring

De auteurs verklaren dat het onderzoek werd uitgevoerd zonder enige commerciële of financiële relatie die als een potentieel belangenconflict kon worden opgevat.

Dankbetuigingen

Wij danken Christine Flury voor het verstrekken van de schapen gegevens en voor nuttige discussie. We danken ook de twee recensenten voor nuttige suggesties om dit document te verbeteren. MB werd ondersteund door het programma Master en Back (Regione Sardegna).