a hidrogénatom oldatai a Schr Xhamdinger egyenlet olyan függvények, amelyek egy gömb harmonikus függvény és egy radiális függvény termékei.

\

a hidrogénatom hullámfunkciói az r, \(\theta\) és \(\varphi \) három változótól és az n, \(l\) és \(m_l\) három kvantumszámtól függenek. A változók megadják az elektron helyzetét a protonhoz képest gömb alakú koordinátákban. A hullámfüggvény abszolút négyzete, \ (/\psi(r, \theta , \varphi )|^2\), \(r\), \(\theta\) és \(\varphi\), megadja a valószínűségi sűrűséget az elektron megtalálására egy \(d \tau\) differenciál térfogatban, az R, \(\theta\) és \(\varphi\) által meghatározott helyzetben.

a kvantumszámoknak nevük van: \(n\) a fő kvantumszám, \(l\) a szögmomentum kvantumszám, és \(m_l\) a mágneses kvantumszám, mert (mint látni fogjuk a 8.4.szakaszban) a mágneses mező energiája függ \(m_l\). Gyakran a \(l\)-t azimutális kvantumszámnak nevezik, mert ez a \(\theta\) – egyenlet következménye, amely magában foglalja az azimutális szöget \(\Theta\), utalva a Zenit szögére.

ezeknek a kvantumszámoknak olyan specifikus értékeik vannak, amelyeket a Schr-egyenletre kivetett fizikai korlátok vagy határfeltételek szabnak meg: \(n\) 0‑nál nagyobb egész számnak kell lennie, \(l\) értéke 0-tól n ‑ 1-ig terjedhet, \(m_l\) értéke pedig \(- l\) – tól \(+l\) – ig terjedhet egység vagy egész lépésben. A \(l\) kvantumszám értékeit általában betűvel kódolják: s jelentése 0, p jelentése 1, d jelentése 2, f jelentése 3; a következő kódok ábécé sorrendben folytatódnak (például g jelentése \(l = 4\)). A kvantumszámok meghatározzák a fizikai mennyiségek kvantálását. A hidrogénatom különböző állapotainak diszkrét energiáit \(n\), a szögmomentum nagyságát \(l\), a szögmomentum egyik komponensét (amelyet a vegyészek általában z‑komponensnek választanak) \(m_l\) adja meg. A \(n\) adott értékű pályák teljes száma \(n^2\).

a hidrogénatom hullámfunkcióit, \(\psi (r, \theta , \varphi )\), atompályáknak nevezzük. Az atomi pálya olyan függvény, amely egy atom elektron leírására szolgál. Az n = 1, \(l=1\) és \(m_l\) = 0 hullámfüggvényt 1s pályának nevezzük, és az ezzel a függvénnyel leírt elektron az ls pályán “benne van”, azaz 1S pályaállapotú. Az \(n\), \(l)\) és \(m_l\) korlátok, amelyeket a hidrogénatom megoldása során szabnak meg, megmagyarázzák, miért van egyetlen 1S pálya, miért van három 2P pálya, öt 3D pálya stb. Látni fogjuk, amikor a 9.fejezetben figyelembe vesszük a többelektronos atomokat, hogy ezek a korlátok magyarázzák a periódusos rendszer jellemzőit. Más szavakkal, a periódusos rendszer a Schr-féle modell megnyilvánulása, valamint a hidrogénatomra vonatkozó Schr-féle Ohdinger-egyenlet megoldásának fizikai korlátai.

egy elektronikus hullámfüggvény variációjának megjelenítése \(r\), \(\theta\) és \(\varphi\) értékekkel azért fontos, mert a hullámfüggvény abszolút négyzete egy atom vagy molekula töltéseloszlását (elektron valószínűségi sűrűségét) ábrázolja. A töltéseloszlás központi szerepet játszik a kémiában, mert összefügg a kémiai reaktivitással. Például egy molekula elektronhiányos része vonzódik egy másik molekula elektronban gazdag régiójához, és az ilyen kölcsönhatások nagy szerepet játszanak a kémiai kölcsönhatásokban, a szubsztitúciós és addíciós reakcióktól a fehérje hajtogatásáig és a szubsztrátok enzimekkel való kölcsönhatásáig.

a hullámfunkciók és a töltéseloszlások vizualizálása kihívást jelent, mivel három változó függvényének viselkedését kell megvizsgálni a háromdimenziós térben. Ezt a vizualizációt megkönnyíti a sugárirányú és szögletes részek külön-külön történő figyelembevétele, de a sugárirányú és szögletes részek külön-külön történő ábrázolása nem tárja fel nagyon jól az orbitális alakját. Az alak jobban feltárható egy valószínűségi sűrűség-diagramban. Egy ilyen háromdimenziós rajz elkészítéséhez ossza fel a helyet kis térfogatú elemekre, számítsa ki a \(\psi^* \psi \) értéket az egyes térfogatelemek közepén, majd árnyékolja, színezze vagy színezze a térfogatelemet a \(\psi^* \psi\) nagyságával arányosan. Ne keverje össze az ilyen parcellákat a poláris parcellákkal, amelyek hasonlóak.

a valószínűségi sűrűségeket kontúrtérképek is ábrázolhatják, amint az a \(\PageIndex{1}\) ábrán látható.

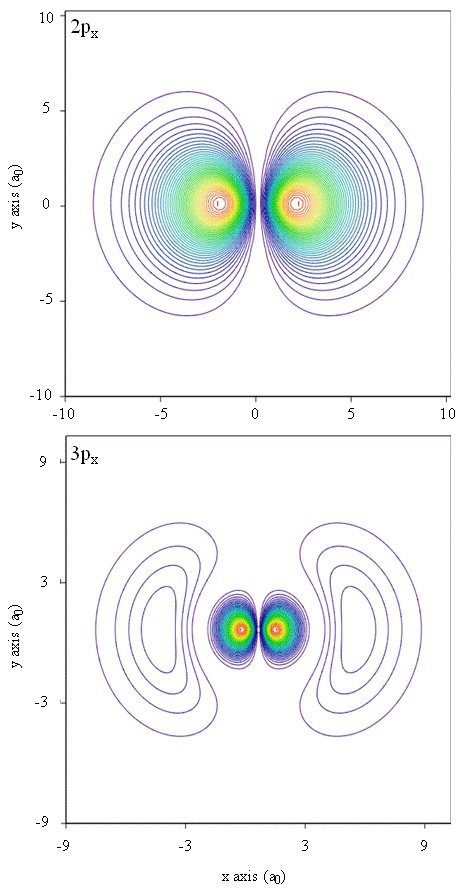
egy másik reprezentációs technika, virtuális valóság modellezés, nagy ígéretet tartogat az elektron sűrűségének ábrázolására. Képzelje el például, hogy képes megtapasztalni az elektron sűrűségét, mint erőt vagy ellenállást egy pálcán, amelyet a háromdimenziós térben mozog. Az ilyen eszközök, az úgynevezett haptikus eszközök, már léteznek, és a tudományos információk képviseletére használják őket. Hasonlóképpen, nem lenne érdekes “repülni” egy atompályán, és megtapasztalni az elektronsűrűség változását a színváltozás vagy a felhősség változásával? Speciálisan kialakított szobák 3D képernyőkkel és “intelligens” szemüveggel, amelyek visszajelzést adnak a néző tekintetének irányáról, jelenleg fejlesztésre kerülnek, hogy lehetővé tegyék számunkra az ilyen érzések megtapasztalását.

az atompályák sugárirányú részeinek külön vizsgálatára szolgáló módszerek hasznos információkat nyújtanak a töltéssűrűség eloszlásáról a pályákon belül. A \(R(r)\) radiális függvények grafikonjai az 1s, 2s és 2p pályákra a \(\PageIndex{2}\) ábrán ábrázolva.

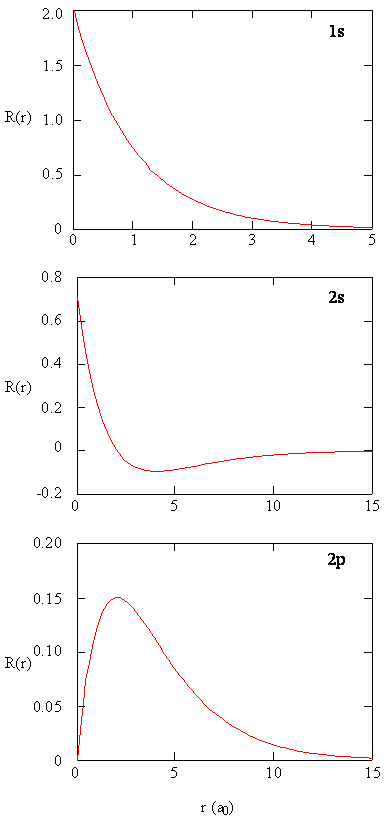
a \(\PageIndex{2}\ ábrán látható 1s függvény magas pozitív értékkel kezdődik a magnál, és exponenciálisan nullára bomlik 5 Bohr sugár után. A mag magas értéke meglepő lehet, de amint később látni fogjuk, az elektron megtalálásának valószínűsége eltűnően kicsi.

következő megjegyzés, hogy a radiális függvény a 2s orbitális, ábra \(\PageIndex{2}\), megy nullára, majd negatívvá válik. Ez a viselkedés feltárja a radiális csomópont jelenlétét a függvényben. Radiális csomópont akkor fordul elő, amikor a radiális függvény nullával egyenlő, kivéve \(r = 0\) vagy \(r = 6\). A csomópontok és az atomi orbitális függvények korlátozó viselkedése egyaránt hasznos annak azonosításában, hogy melyik orbitát melyik hullámfüggvény írja le. Például az összes s függvénynek nem nulla hullámfüggvény-értéke van \(r = 0\), de a P, d, f és az összes többi függvény nullára megy az eredetnél. Hasznos megjegyezni, hogy vannak\ (n-1-l\) radiális csomópontok egy hullámfüggvényben, ami azt jelenti, hogy az 1s orbitálnak nincs radiális csomópontja, a 2s-nek van egy radiális csomópontja stb.

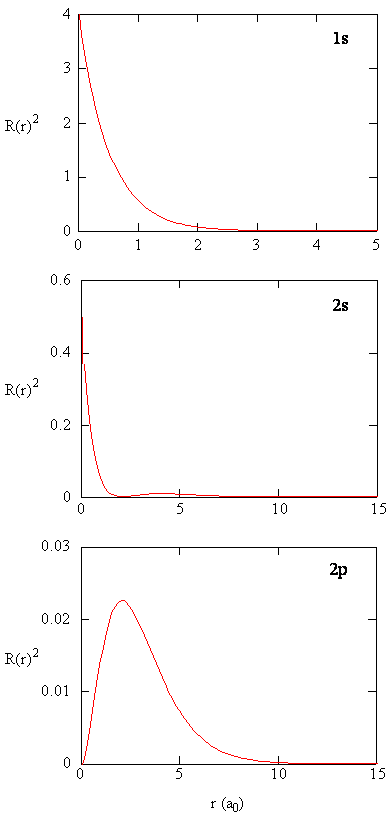
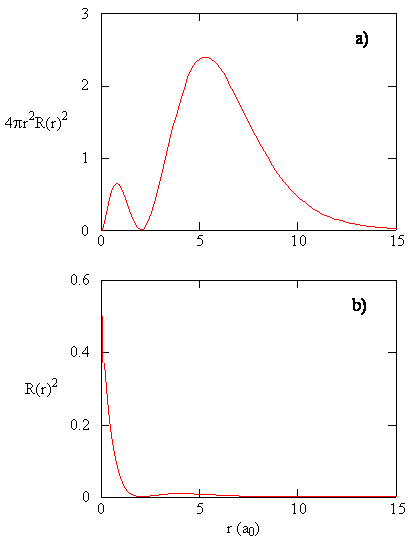
a mennyiség \(R(r) ^* R(r)\) adja meg a radiális valószínűségi sűrűséget; vagyis annak a valószínűségi sűrűségnek, hogy az elektron a protontól \(r\) távolságban helyezkedik el. Az ábrán három típusú atompálya radiális valószínűségi sűrűségét ábrázoljuk (\PageIndex{3}\).

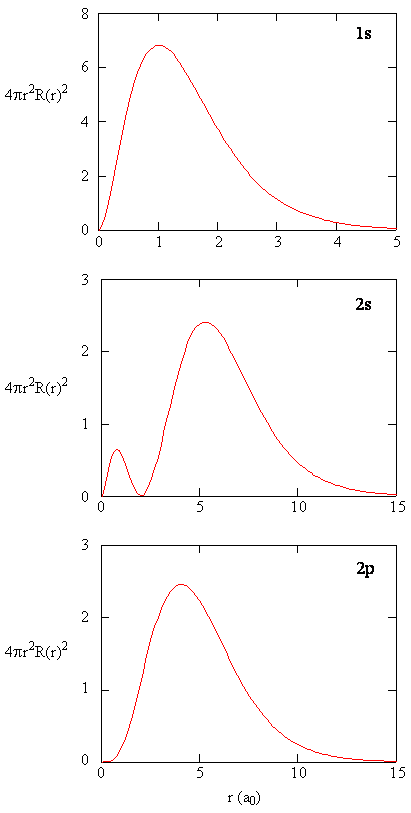
amikor az r minden értékének radiális valószínűségi sűrűségét megszorozzuk a gömbfelület azon területével, amelyet az adott R érték képvisel, megkapjuk a radiális eloszlási függvényt. A radiális eloszlási függvény megadja annak valószínűségi sűrűségét, hogy egy elektron bárhol megtalálható legyen a gömb felületén, amely távolságra van r a protontól. Mivel a gömbfelület területe \(4 \ pi r^2\), a radiális eloszlási függvényt \(4 \pi r^2 R(r) ^* R(r)\) adja meg.

a radiális eloszlási függvények A \(\PageIndex{4}\) ábrán láthatók. Kis értékeknél r, a radiális eloszlási függvény alacsony, mert a kis sugarak kis felülete modulálja a radiális valószínűségi sűrűségfüggvény magas értékét a mag közelében. Ahogy növeljük \(r\), az adott r értékhez társított felület növekszik, és az \(r^2\) kifejezés a radiális eloszlási függvény növekedését eredményezi, annak ellenére, hogy a radiális valószínűségi sűrűség csökkenni kezd. Nagy \(r\) értékeknél a radiális függvény exponenciális bomlása meghaladja a \(r^2\) kifejezés által okozott növekedést, és a radiális eloszlási függvény csökken.