minden regressziós technika egyetlen kimeneti (válasz) változót és egy vagy több input (prediktor) változót tartalmaz. A kimeneti változó numerikus. Az Általános regressziós faépítési módszertan lehetővé teszi, hogy a bemeneti változók folytonos és kategorikus változók keverékét képezzék. Döntési fa akkor jön létre, amikor a fa minden döntési csomópontja tartalmaz egy tesztet valamilyen bemeneti változó értékére. A fa terminál csomópontjai tartalmazzák az előre jelzett kimeneti változó értékeket.

a regressziós fa a döntési fák egyik változatának tekinthető, amelynek célja a valós értékű függvények közelítése, ahelyett, hogy osztályozási módszerekhez használnák.

módszertan

a regressziós fa az úgynevezett folyamaton keresztül épül fel bináris rekurzív particionálás, amely egy iteratív folyamat, amely felosztja az adatokat partíciókra vagy ágakra, majd folytatja az egyes partíció kisebb csoportokra osztását, amikor a módszer felfelé halad minden ágon.

kezdetben a képzési készlet összes rekordja (előre Osztályozott rekordok, amelyek a fa szerkezetének meghatározására szolgálnak) ugyanabba a partícióba vannak csoportosítva. Az algoritmus ezután elkezdi az adatok kiosztását az első két partícióba vagy ágba, minden lehetséges bináris felosztást felhasználva minden mezőn. Az algoritmus kiválasztja azt a felosztást, amely minimalizálja a négyzetes eltérések összegét a két különálló partíció átlagától. Ezt a felosztási szabályt ezután minden új ágra alkalmazzák. Ez a folyamat addig folytatódik, amíg minden csomópont el nem éri a felhasználó által megadott minimális csomópontméretet, és terminálcsomóponttá nem válik. (Ha egy csomópont átlagától való négyzetelt eltérések összege nulla, akkor az a csomópont akkor is terminálcsomópontnak tekinthető, ha nem érte el a minimális méretet.)

a fa metszése

mivel a fát az Edzőkészletből termesztik, egy teljesen kifejlett fa általában túlzott illeszkedéstől szenved (vagyis az Edzőkészlet véletlenszerű elemeit magyarázza, amelyek valószínűleg nem a nagyobb populáció jellemzői). Ez a túlzott illesztés A valós adatok gyenge teljesítményét eredményezi. Ezért a fát meg kell metszeni az érvényesítési készlet segítségével. XLMiner kiszámítja a költség komplexitás tényező minden lépésben a növekedés során a fa, és úgy dönt, hogy hány döntési csomópontok a metszett fa. A költség komplexitási tényező az a multiplikatív tényező, amelyet a fa méretére alkalmaznak (a terminálcsomópontok számával mérve).

a fát úgy metszjük meg, hogy minimalizáljuk a következők összegét: 1) A kimeneti változó varianciája az érvényesítési adatokban, egyszerre egy terminálcsomópontot veszünk; és 2) a költség komplexitási tényező szorzata és a terminálcsomópontok száma. Ha a költség komplexitási tényező nulla, akkor a metszés egyszerűen megtalálja azt a fát, amely a legjobban teljesít az érvényesítési adatokon a teljes terminálcsomópont-variancia szempontjából. A költség-komplexitási tényező nagyobb értékei kisebb fákat eredményeznek. A metszést utoljára először hajtják végre, vagyis az utoljára termesztett csomópont az első, amelyet el kell távolítani.

Ensemble Methods

az XLMiner V2015 három hatékony ensemble módszert kínál a regressziós fák használatához: zsákolás (bootstrap aggregálás), fellendítés és véletlenszerű fák. A regressziós fa algoritmus felhasználható egy olyan modell megtalálására, amely jó előrejelzéseket eredményez az új adatokra vonatkozóan. Megnézhetjük az aktuális prediktor statisztikáit és zavartsági mátrixait, hogy lássuk, a modellünk jól illeszkedik-e az adatokhoz; de honnan tudhatnánk, hogy van-e jobb prediktor, amely csak arra vár, hogy megtaláljuk? A válasz az, hogy nem tudjuk, létezik-e jobb előrejelző. Az együttes módszerek azonban lehetővé teszik számunkra, hogy több gyenge regressziós fa modellt kombináljunk, amelyek együttesen új, pontos, erős regressziós fa modellt alkotnak. Ezek a módszerek több különböző regressziós modell létrehozásával működnek, az eredeti adatkészlet különböző mintáinak vételével, majd a kimenetek kombinálásával. (A kimenetek több technikával kombinálhatók, például a többség az osztályozásra és a regresszió átlagolására szavaz) ez a modellkombináció hatékonyan csökkenti az erős modell varianciáját. Az xlminer-ben kínált három típusú együttes módszer (zsákolás ,növelés és véletlenszerű fák) három tételben különbözik egymástól: 1) Az egyes prediktorok vagy gyenge modellek képzési készletének kiválasztása; 2) a gyenge modellek generálása; és 3) a kimenetek kombinálása. Mindhárom módszernél minden gyenge modellt a teljes képzési készleten kiképeznek, hogy jártasak legyenek az adatkészlet bizonyos részében.

a zsákolás (bootstrap aggregálás) volt az egyik első ensemble algoritmus, amelyet valaha írtak. Ez egy egyszerű algoritmus, mégis nagyon hatékony. A zsákolás több képzési készletet generál véletlenszerű mintavételezéssel cserével (bootstrap mintavétel), alkalmazza a regressziós fa algoritmust minden adatkészletre, majd a modellek átlagát veszi figyelembe az új adatok előrejelzéseinek kiszámításához. A zsákolás legnagyobb előnye, hogy az algoritmus viszonylag könnyen párhuzamosítható, ami jobb választást jelent a nagyon nagy adatkészletek számára.

A Boosting erős modellt épít fel egymás után képzési modellekkel, hogy a korábbi modellekben pontatlan előrejelzett értékeket kapó rekordokra koncentráljon. Miután elkészült, az összes előrejelzőt súlyozott többségi szavazattal kombinálják. XLMiner kínál három változata fellendítése által megvalósított AdaBoost algoritmus (az egyik legnépszerűbb ensemble algoritmusok ma használt): M1 (Freund), M1 (Breiman), és SAMME (Stagewise additív modellezés egy Multi-osztály exponenciális).

Adaboost.Az M1 először súlyt (wb(i)) rendel minden rekordhoz vagy megfigyeléshez. Ez a súly eredetileg 1/n-re van állítva, és az algoritmus minden iterációján frissül. Egy eredeti regressziós fa jön létre ezzel az első betanítási készlettel (Tb), és a hibát a következőképpen számítják ki:

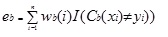
ahol az I () függvény 1-et ad vissza, ha igaz, és 0-t, ha nem.

a regressziós fa hibáját a B-edik iterációban használják az állandó kiszámításához ?b. Ez az állandó a súly frissítésére szolgál(wb (i). Adaboostban.M1 (Freund), az állandó kiszámítása:

ab= ln((1-eb)/eb)

az AdaBoost-ban.M1 (Breiman), az állandó kiszámítása:

ab= 1/2LN ((1-eb)/eb)

a SAMME-ban az állandó kiszámítása:

ab= 1/2LN ((1-eb)/eb + ln (k-1), ahol k az osztályok száma

ahol a kategóriák száma egyenlő 2-vel, SAMME ugyanúgy viselkedik, mint Adaboost Breiman.

A három implementáció bármelyikében (Freund, Breiman vagy SAMME) a (b + 1)iteráció új súlya

ezután a súlyokat mind 1 összegére módosítják. Ennek eredményeként a pontatlan előrejelzett értékekhez rendelt megfigyelésekhez rendelt súlyok növekednek, a pontos előrejelzett értékekhez rendelt megfigyelésekhez rendelt súlyok pedig csökkennek. Ez a kiigazítás arra kényszeríti a következő regressziós modellt, hogy nagyobb hangsúlyt fektessen a pontatlan előrejelzésekhez rendelt rekordokra. (Ez ? az állandót a végső számításban is használják, amely a legalacsonyabb hibával rendelkező regressziós modellnek nagyobb befolyást biztosít.) Ez a folyamat addig ismétlődik, amíg b = a gyenge tanulók száma. Az algoritmus ezután kiszámítja az összes gyenge tanuló súlyozott átlagát, és ezt az értéket hozzárendeli a rekordhoz. A fellendítés általában jobb modelleket eredményez, mint a zsákolás; ennek azonban van hátránya, mivel nem párhuzamosítható. Ennek eredményeként, ha a gyenge tanulók száma nagy, a növelés nem lenne megfelelő.

a véletlenszerű fák módszer (véletlenszerű erdők) a zsákolás változata. Ez a módszer úgy működik, hogy több gyenge regressziós fát betanít egy rögzített számú véletlenszerűen kiválasztott jellemzővel (sqrt az osztályozáshoz és a jellemzők száma/3 az előrejelzéshez), majd veszi a gyenge tanulók átlagértékét, és ezt az értéket hozzárendeli az erős előrejelzőhöz. A keletkezett gyenge fák száma általában több száztól több ezerig terjedhet, az edzőkészlet méretétől és nehézségétől függően. A véletlenszerű fák párhuzamosíthatók, mivel ezek a zsákolás egyik változata. Mivel azonban a tandom trees korlátozott mennyiségű funkciót választ ki az egyes iterációkban, a véletlenszerű fák teljesítménye gyorsabb, mint a zsákolás.

a regressziós Faegyüttes módszerek nagyon hatékony módszerek, és általában jobb teljesítményt eredményeznek, mint egyetlen fa. Ez a funkció mellett XLMiner V2015 pontosabb előrejelzési modellek, és figyelembe kell venni az egyetlen fa módszer.