bizonyos körülmények között a toroid induktor tekercsében lévő áram csak a tekercseken belüli B mezőhöz járul hozzá, és nem járul hozzá a tekercseken kívüli mágneses B mezőhöz. Ez a szimmetria és az AMP Intravitalis törvény következménye.

megfelelő feltételek A B mező teljes belső bezárásához

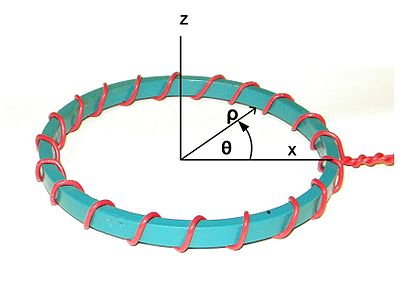ábra. 1. Koordináta-rendszer. A Z tengely a szimmetria névleges tengelye. Az X tengely választott önkényesen egy vonalba a kiindulási pont a tekercselés. az ún. radiális irány. a körülhatárolt iránynak nevezzük a körülhatárolt irányt.

Fig. 2. Tengelyirányban szimmetrikus toroid induktor, kerületi áram nélkül.

a kerületi áram hiánya (a kerületi áram útját a szakasz 3.ábráján piros nyíl jelzi), valamint a vezetők és a mágneses anyagok axiálisan szimmetrikus elrendezése elegendő feltétel a B mező teljes belső bezárásához. (Egyes szerzők inkább a H mezőt használják). A szimmetria miatt a B fluxus vonalainak állandó intenzitású köröket kell alkotniuk a szimmetriatengely középpontjában. A B fluxus egyetlen vonala, amely bármilyen áramot körülvesz, azok, amelyek a toroid tekercsben vannak. Ezért Amper circuital törvényéből a b mező intenzitásának nullának kell lennie a tekercseken kívül.

Fig. 3. Kerületi árammal rendelkező toroid induktor

e szakasz 3. ábrája mutatja a leggyakoribb toroid tekercselést. Nem felel meg a teljes b mező bezárásának mindkét követelményének. A tengelyről nézve a tekercselés néha a mag belsejében, néha pedig a mag külső oldalán található. A közeli régióban nem axiálisan szimmetrikus. A tekercselési távolság többszörösének megfelelő pontokon azonban a toroid szimmetrikusnak tűnik. Még mindig fennáll a kerületi áram problémája. Nem számít, hányszor veszi körül a tekercselés a magot, függetlenül attól, hogy milyen vékony a huzal, ez a toroid induktor továbbra is tartalmaz egy tekercshurkot a toroid síkjában. Ez a tekercselés az induktor síkjában egy E mezőre is érzékeny lesz.

a 4-6. ábra a kerületi áram semlegesítésének különböző módjait mutatja. A 4. ábra a legegyszerűbb, amelynek az az előnye, hogy a visszatérő vezetéket az induktor megvásárlása vagy megépítése után lehet hozzáadni.

Fig. 4. A kerületi áram ellentétes egy visszatérő vezetékkel. A huzal fehér, és az induktor külső pereme és a tekercs külső része között fut.

Fig. 5. A kerületi áram visszatérő tekercseléssel ellensúlyozva.

Fig. 6. Kerületi áram ellensúlyozva osztott visszatérő tekercseléssel.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

a tekercselés mentén a potenciál eloszlik. Ez E-mezőhöz vezethet a toroid síkjában, valamint a toroid síkjában lévő E mezőre való hajlamhoz, amint azt a 7.ábra mutatja. Ezt a 8. ábrán látható visszacsévéléssel lehet enyhíteni. Ezzel a tekercseléssel minden egyes helyen a tekercs keresztezi magát, a két rész egyenlő és ellentétes polaritású lesz, ami jelentősen csökkenti a síkban keletkező E mezőt.

toroid induktor/transzformátor és mágneses vektor potenciáledit

a szimmetrikus toroid induktor körüli mágneses vektorpotenciál fejlődését mutatja be.

lásd Feynman 14.és 15. fejezetét a mágneses vektorpotenciál általános megvitatásához. Lásd Feynman 15-11. oldal a mágneses vektorpotenciál diagramját egy hosszú vékony mágnesszelep körül, amely a b mező teljes belső elzáródását is mutatja, legalábbis a végtelen határban.

az A mező pontos, ha a feltételezést használjuk b f a = 0 {\displaystyle bf{a}=0}

. Ez a következő feltételezések szerint igaz:

• 1. a Coulomb nyomtáv
• 2. A Lorenz-nyomtávot használjuk, és nincs töltéseloszlás, 6 = 0 {\displaystyle \ rho =0\,}
  
• 3. A Lorenz mérőt használjuk, és nulla frekvenciát feltételezünk
• 4. A Lorenz-nyomtávot használjuk, és egy olyan nem nulla frekvenciát, amely elég alacsony ahhoz, hogy figyelmen kívül hagyja az 1 c 2-T! \T! \t {\displaystyle {\frac {\1}{c^{2}}} {\frac {\parcial\Phi} {\parcial t}}}
  

  .

a 4.számot a szakasz többi részében kell feltételezni, és hivatkozni lehet a “kvázi-statikus állapotra”.

bár a tengelyirányban szimmetrikus toroid induktor kerületi áram nélkül teljesen korlátozza a B mezőt a tekercseken belül, az A mező (mágneses vektorpotenciál) nem korlátozódik. A képen az 1. nyíl a vektorpotenciált ábrázolja a szimmetria tengelyén. Az A és B sugárirányú áramszakaszok egyenlő távolságra vannak a tengelytől, de ellentétes irányba mutatnak, így megszakadnak. A c és a d szegmens is megszűnik. Valójában az összes radiális áramszegmens megszűnik. Az axiális áramok helyzete más. A toroid külső oldalán lévő axiális áram lefelé, a toroid belsejében lévő axiális áram pedig felfelé mutat. A toroid külső oldalán lévő minden tengelyirányú áramszegmens kiegyenlíthető egy egyenlő, de ellentétesen irányított szegmenssel a toroid belsejében. A belső szegmensek közelebb vannak a tengelyhez, mint a külső szegmensek, ezért az a mező nettó felfelé irányuló komponense van a szimmetriatengely mentén.

a kör keresztmetszetű toroid induktor körüli mágneses vektorpotenciál (a), mágneses fluxus (B) és áramsűrűség (j) mezőket képviseli. A vastagabb vonalak nagyobb átlagos intenzitású terepi vonalakat jeleznek. Körök keresztmetszete a mag képviseli B fluxus jön ki a képből. Plusz jelek a másik keresztmetszete a mag képviseli B fluxus megy a képbe. Div a = 0 feltételezték.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. 0 {\displaystyle {\frac {\parciális e}{\parciális t}}\rightarrow 0}

) azonos formájúak, akkor az a vonalai és kontúrjai B-hez kapcsolódnak, mint a B vonalai és kontúrjai j-hez. így az a mező ábrázolása a B fluxus hurokja körül (ahogy egy toroid induktorban előállítanák) minőségileg megegyezik a b mező az áramhurok körül. A bal oldali ábra egy művész ábrázolása az a mezőről egy toroid induktor körül. A vastagabb vonalak nagyobb átlagos intenzitású utakat jelölnek (a rövidebb utak nagyobb intenzitással rendelkeznek, így az útvonal integrálja megegyezik). A vonalak csak húzott, hogy jól nézzen ki, és kölcsönöz általános megjelenés az A területen.

Toroid transzformátor hatása teljes B mezőzárás jelenlétében

az E és B mezők kiszámíthatók az A és az A és az a {\displaystyle \phi \,}

(skaláris elektromos potenciál) mezőkből B = A . {\displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {A} .}

és : E = − ~ − ~ a ~ T {\displaystyle \mathbf {e} =-\nabla \Phi -{\frac {\parciális \mathbf {a} }{\parciális t}}}

így még akkor is, ha a tekercseken kívüli Régió mentes B mezőtől, akkor nem nulla e mezővel van kitöltve. {\Displaystyle {\frac {\parciális \mathbf {a} }{\parciális t}}}

az elsődleges és a másodlagos mágneses tér összekapcsolásáért felelős, míg a mennyiség (\\displaystyle \nabla \ Phi\,}

felelős a primer és szekunder közötti nemkívánatos elektromos mező csatolásért. A transzformátor tervezői megpróbálják minimalizálni az elektromos mező kapcsolását. Ennek a szakasznak a többi részében a \{\displaystyle \nabla \ Phi\,}

nullának kell tekinteni, hacsak másként nem jelezzük.

Stokes-tétel érvényes, úgy, hogy az út integrálja a egyenlő a zárt B fluxussal, ugyanúgy, mint az út integrálja B egyenlő a zárt áram állandó szorzatával

az út integrálja E a szekunder tekercs mentén megadja a szekunder indukált EMF-jét (Elektro-hajtóerő).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

ami azt mondja, hogy az EMF megegyezik a tekercs által körülvett B fluxus változásának időbeli sebességével, ami a szokásos eredmény.

Toroid transzformátor Poynting vektor csatolás az elsődlegesből a másodlagosba a teljes B mezőzár jelenlétében

ezen az ábrán, a kék pontok azt jelzik, hogy az elsődleges áramból származó B fluxus hol jön ki a képből, a plusz jelek pedig azt jelzik, hogy hova kerül a képbe.

az ábra Magyarázataszerkesztés

Ez az ábra egy toroid transzformátor félszakaszát mutatja. Kvázi statikus feltételeket feltételezünk, tehát az egyes mezők fázisa mindenütt azonos. A transzformátor, a tekercsek és minden dolog szimmetrikusan oszlik el a szimmetriatengely körül. A tekercsek olyanok, hogy nincs kerületi áram. A követelmények teljesülnek A B mező teljes belső bezárásához az elsődleges áram miatt. A mag és az elsődleges tekercset a szürke-barna tórusz képviseli. Az elsődleges tekercselés nem látható, de a tekercsben lévő áram a keresztmetszet felületén arany (vagy narancssárga) ellipszisként jelenik meg. Az elsődleges áram által okozott B mező teljes egészében az elsődleges tekercs (azaz a mag) által körülvett régióra korlátozódik. A bal oldali keresztmetszet kék pontjai azt jelzik, hogy a magban lévő B fluxus vonalak a bal oldali keresztmetszetből származnak. A másik keresztmetszetben a kék plusz jelek azt jelzik, hogy a B fluxus belép oda. Az elsődleges áramokból származó e mező zöld ellipszisként jelenik meg. A szekunder tekercset barna vonalként mutatjuk be, amely közvetlenül a szimmetriatengelyen halad. A szokásos gyakorlatban a szekunder két végét egy hosszú huzallal kötik össze, amely jól távol marad a tórustól, de az abszolút axiális szimmetria fenntartása érdekében az egész készüléket úgy képzeljük el, hogy egy tökéletesen vezető gömb belsejében van, a szekunder huzallal pedig mindkét végén a gömb belsejébe “földelve”. A szekunder ellenállási huzalból készül, így nincs külön terhelés. Az e mező a szekunder mentén áramot okoz a szekunderben (sárga nyilak), ami B mezőt okoz a szekunder körül (kék ellipszisként látható). Ez a b mező kitölti a teret, beleértve a transzformátor magját is, így végül folyamatos, nem nulla b mező van az elsődlegestől a szekunder felé, ha a szekunder nincs nyitva. Az e mező keresztterméke (elsődleges áramokból származik) és a b mező (másodlagos áramokból származik) képezi a Poynting vektort, amely az elsődlegesről a másodlagos felé mutat.