8.2: Le funzioni d’onda
Le soluzioni all’equazione di Schrödinger dell’atomo di idrogeno sono funzioni che sono prodotti di una funzione armonica sferica e di una funzione radiale.
\
Le funzioni d’onda per l’atomo di idrogeno dipendono dalle tre variabili r, \(\theta\) e \(\varphi \) e dai tre numeri quantici n, \(l\) e \(m_l\). Le variabili danno la posizione dell’elettrone rispetto al protone in coordinate sferiche. Il quadrato assoluto della funzione d’onda, \(| \psi (r, \theta , \varphi )|^2\), valutato a \(r\), \(\theta\) e \(\varphi\) fornisce la densità di probabilità di trovare l’elettrone all’interno di un volume differenziale \(d \tau\), centrato nella posizione specificata da r, \(\theta\) e \(\varphi\).
Esercizio \(\PageIndex{1}\)
Qual è il valore dell’integrale
\
I numeri quantici hanno nomi: \(n\) è chiamato il numero quantico principale, \(l\) è chiamato il numero quantico del momento angolare e \(m_l\) è chiamato il numero quantico magnetico perché (come vedremo nella Sezione 8.4) l’energia in un campo magnetico dipende da \(m_l\). Spesso \(l\) è chiamato il numero quantico azimutale perché è una conseguenza dell’equazione \(\theta\), che coinvolge l’angolo azimutale \(\Theta \), riferendosi all’angolo allo zenit.
Questi numeri quantici hanno valori specifici che sono dettati dai vincoli fisici o dalle condizioni al contorno imposte all’equazione di Schrödinger: \(n\) deve essere un numero intero maggiore di 0, \(l\) può avere i valori da 0 a n‑1 e \(m_l\) può avere \(2l + 1\) valori che vanno da \(- l\) ‑ a \(+l\) in passi di unità o interi. I valori del numero quantico \(l\) di solito sono codificati da una lettera: s significa 0, p significa 1, d significa 2, f significa 3; i codici successivi continuano in ordine alfabetico (ad esempio, g significa \(l = 4\)). I numeri quantici specificano la quantizzazione delle grandezze fisiche. Le energie discrete dei diversi stati dell’atomo di idrogeno sono date da \(n\), la grandezza del momento angolare è data da \(l\) e una componente del momento angolare(solitamente scelta dai chimici per essere la componente z) è data da \(m_l\). Il numero totale di orbitali con un particolare valore di \(n\) è \(n^2\).
Esercizio \(\PageIndex{2}\)
Considera diversi valori per n e mostra che il numero di orbitali per ogni n è \(n^2\).
Esercizio \(\PageIndex{3}\)
Costruisci una tabella che riassume i valori consentiti per i numeri quantici n, \(l\) e \(m_l\). per i livelli energetici da 1 a 7 dell’idrogeno.
Esercizio \(\PageIndex{4}\)
La notazione 3d specifica i numeri quantici per un elettrone nell’atomo di idrogeno. Quali sono i valori per n e \(l\)? Quali sono i valori per l’energia e il momento angolare? Quali sono i possibili valori per il numero quantico magnetico? Quali sono i possibili orientamenti per il vettore del momento angolare?
Le funzioni d’onda dell’atomo di idrogeno, \(\psi (r, \theta , \varphi )\), sono chiamate orbitali atomici. Un orbitale atomico è una funzione che descrive un elettrone in un atomo. La funzione d’onda con n = 1, \(l=1\) e \(m_l\) = 0 è chiamata orbitale 1s, e un elettrone descritto da questa funzione si dice che sia “in” l’orbitale ls, cioè abbia uno stato orbitale 1s. I vincoli su \(n\), \(l)\) e \(m_l\) che vengono imposti durante la soluzione dell’equazione di Schrödinger dell’atomo di idrogeno spiegano perché esiste un singolo orbitale 1s, perché ci sono tre orbitali 2p, cinque orbitali 3d, ecc. Vedremo quando consideriamo gli atomi multi-elettroni nel Capitolo 9 che questi vincoli spiegano le caratteristiche della Tavola periodica. In altre parole, la Tavola Periodica è una manifestazione del modello di Schrödinger e dei vincoli fisici imposti per ottenere le soluzioni all’equazione di Schrödinger per l’atomo di idrogeno.
Visualizzare la variazione di una funzione d’onda elettronica con \(r\), \(\theta\) e \(\varphi\) è importante perché il quadrato assoluto della funzione d’onda descrive la distribuzione di carica (densità di probabilità degli elettroni) in un atomo o molecola. La distribuzione della carica è fondamentale per la chimica perché è correlata alla reattività chimica. Ad esempio, una parte carente di elettroni di una molecola è attratta da una regione ricca di elettroni di un’altra molecola e tali interazioni svolgono un ruolo importante nelle interazioni chimiche che vanno dalle reazioni di sostituzione e aggiunta al ripiegamento delle proteine e all’interazione di substrati con enzimi.
Visualizzare le funzioni d’onda e le distribuzioni di carica è difficile perché richiede l’esame del comportamento di una funzione di tre variabili nello spazio tridimensionale. Questa visualizzazione è facilitata considerando separatamente le parti radiali e angolari, ma tracciare separatamente le parti radiali e angolari non rivela molto bene la forma di un orbitale. La forma può essere rivelata meglio in un diagramma di densità di probabilità. Per creare una trama tridimensionale, dividere lo spazio in piccoli elementi di volume, calcolare \(\psi^ * \ psi\) al centro di ciascun elemento di volume, quindi ombreggiare, stipple o colorare quell’elemento di volume in proporzione alla grandezza di \(\psi^* \psi \). Non confondere tali trame con trame polari, che sembrano simili.
Le densità di probabilità possono anche essere rappresentate da mappe di contorno, come mostrato in Figura \(\PageIndex{1}\).
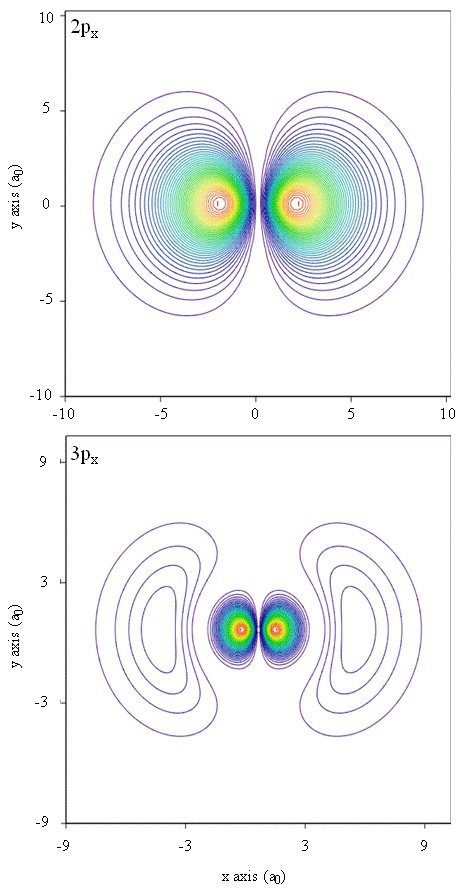
Un’altra tecnica di rappresentazione, la modellazione della realtà virtuale, ha una grande promessa per la rappresentazione delle densità di elettroni. Immagina, ad esempio, di essere in grado di sperimentare la densità elettronica come forza o resistenza su una bacchetta che ti muovi attraverso lo spazio tridimensionale. Dispositivi come questi, chiamati dispositivi aptici, esistono già e vengono utilizzati per rappresentare informazioni scientifiche. Allo stesso modo, non sarebbe interessante “volare” attraverso un orbitale atomico e sperimentare cambiamenti nella densità elettronica come cambiamenti di colore o cambiamenti di nuvolosità? Sono attualmente in fase di sviluppo stanze appositamente progettate con schermi 3D e occhiali “intelligenti” che forniscono feedback sulla direzione dello sguardo dello spettatore per permetterci di provare tali sensazioni.
I metodi per esaminare separatamente le porzioni radiali degli orbitali atomici forniscono informazioni utili sulla distribuzione della densità di carica all’interno degli orbitali. Grafici delle funzioni radiali, \(R (r)\), per gli orbitali 1s, 2s e 2p tracciati nella figura \(\PageIndex{2}\).
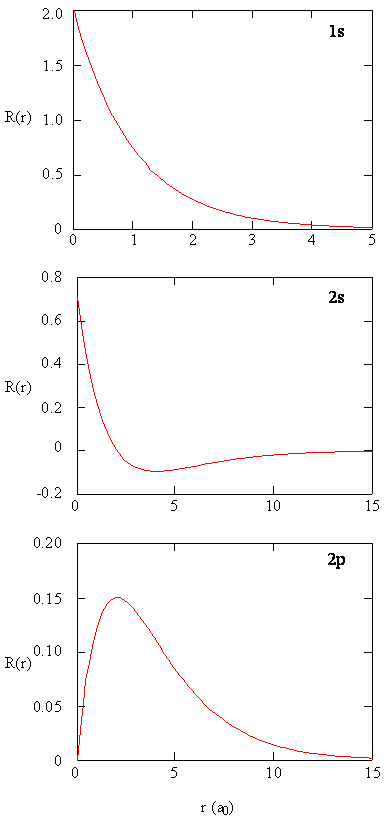
La funzione 1s in Figura \(\PageIndex{2}\) inizia con un alto valore positivo al nucleo e decade esponenzialmente a zero dopo 5 raggi di Bohr. L’alto valore al nucleo può essere sorprendente, ma come vedremo più avanti, la probabilità di trovare un elettrone al nucleo è incredibilmente piccola.
Si noti successivamente come la funzione radiale per l’orbitale 2s, Figura \(\PageIndex{2}\), va a zero e diventa negativa. Questo comportamento rivela la presenza di un nodo radiale nella funzione. Un nodo radiale si verifica quando la funzione radiale è uguale a zero diverso da \ (r = 0\) o \(r=∞\). I nodi e i comportamenti limitanti delle funzioni orbitali atomiche sono entrambi utili per identificare quale orbitale viene descritto con quale funzione d’onda. Ad esempio, tutte le funzioni s hanno valori di funzione d’onda diversi da zero a \(r = 0\), ma p, d, f e tutte le altre funzioni vanno a zero all’origine. È utile ricordare che ci sono nodi radiali \(n-1-l\) in una funzione d’onda, il che significa che un orbitale 1s non ha nodi radiali, un 2s ha un nodo radiale e così via.
Exercise \(\PageIndex{5}\)
Esamina le forme matematiche delle funzioni d’onda radiali. Quale caratteristica nelle funzioni fa sì che alcune di esse vadano a zero all’origine mentre le funzioni s non vanno a zero all’origine?
Esercizio \(\PageIndex{6}\)
Quale caratteristica matematica di ciascuna delle funzioni radiali controlla il numero di nodi radiali?
Esercizio \(\PageIndex{7}\)
A quale valore di r si verifica il nodo radiale 2s?
Esercizio \(\PageIndex{8}\)
Crea una tabella che fornisce l’energia, il numero di nodi radiali e il numero di nodi angolari e il numero totale di nodi per ogni funzione con n = 1, 2 e 3. Identificare la relazione tra l’energia e il numero di nodi. Identificare la relazione tra il numero di nodi radiali e il numero di nodi angolari.
La quantità \(R (r) ^* R(r)\) dà la densità di probabilità radiale; cioè, la densità di probabilità per l’elettrone di essere in un punto situato la distanza \(r\) dal protone. Le densità di probabilità radiale per tre tipi di orbitali atomici sono tracciate in Figura (\PageIndex{3}\).
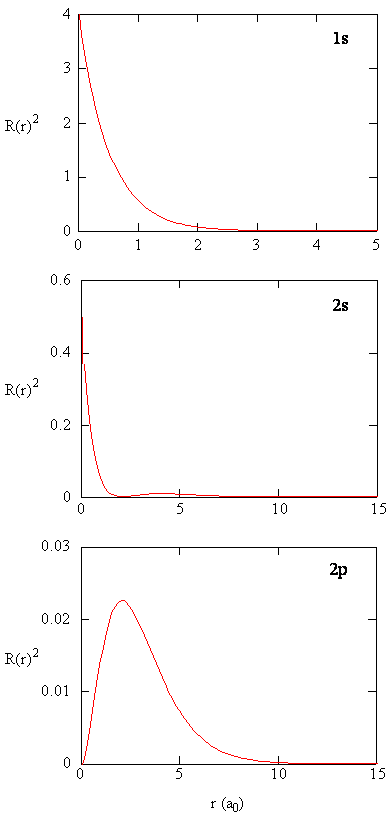
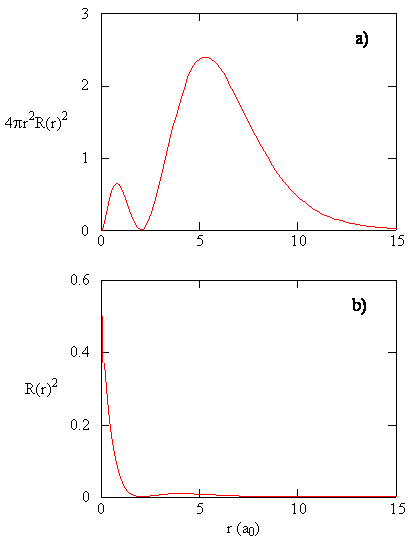
Quando la densità di probabilità radiale per ogni valore di r viene moltiplicata per l’area della superficie sferica rappresentata da quel particolare valore di r, otteniamo la funzione di distribuzione radiale. La funzione di distribuzione radiale fornisce la densità di probabilità per un elettrone che si trova ovunque sulla superficie di una sfera situata a una distanza r dal protone. Poiché l’area di una superficie sferica è \(4 \pi r^2\), la funzione di distribuzione radiale è data da \(4 \pi r^2 R(r) ^* R(r)\).
Le funzioni di distribuzione radiale sono mostrate nella figura \(\PageIndex{4}\). A piccoli valori di r, la funzione di distribuzione radiale è bassa perché la piccola area di superficie per i piccoli raggi modula l’alto valore della funzione di densità di probabilità radiale vicino al nucleo. Man mano che aumentiamo \(r\), l’area di superficie associata a un dato valore di r aumenta e il termine \(r^2\) fa aumentare la funzione di distribuzione radiale anche se la densità di probabilità radiale inizia a diminuire. A grandi valori di \(r\), il decadimento esponenziale della funzione radiale supera l’aumento causato dal termine \(r^2\) e la funzione di distribuzione radiale diminuisce.
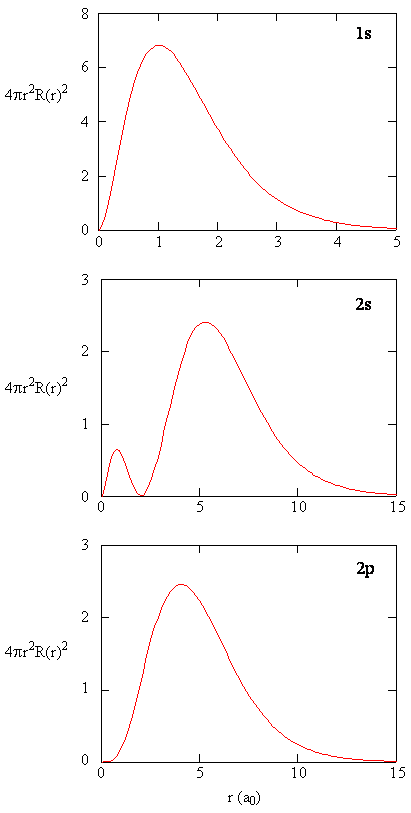
Exercise \(\PageIndex{9}\)
Scrivi un confronto di qualità tra la funzione radiale e la funzione di distribuzione radiale per l’orbitale 2s. Vedi Figura (\PageIndex {5}\)
Contributori e attribuzioni
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (“Stati quantici di atomi e molecole”)