Le antenne irradiano energia elettromagnetica per trasmettere o ricevere informazioni. Pertanto, i termini Energia e Potenza sono associati a queste onde elettromagnetiche e dobbiamo discuterne. Un’onda elettromagnetica ha sia campi elettrici che magnetici.

Considera l’onda in qualsiasi istante, che può essere visualizzata in entrambi i vettori. La figura seguente mostra la rappresentazione dei componenti del campo elettrico e magnetico in un’onda elettromagnetica.

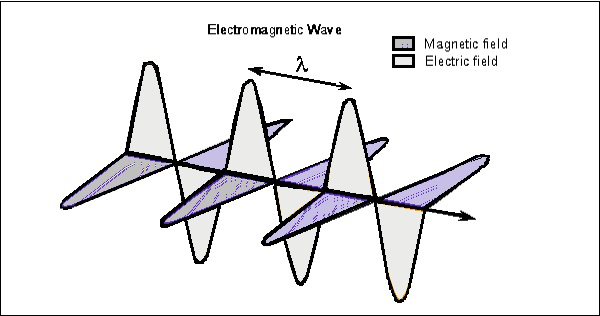
L’onda elettrica è presente verticale alla propagazione dell’onda EM, mentre l’onda magnetica è posizionata orizzontalmente. Entrambi i campi sono ad angolo retto l’uno rispetto all’altro.

Vettore di Poynting

Il vettore di Poynting descrive l’energia dell’onda EM per unità di tempo per unità di area in un dato istante di tempo. John Henry Poynting prima derivato questo vettore nel 1884 e quindi è stato chiamato dopo di lui.

Definizione – “Il vettore di Poynting fornisce la velocità di trasferimento di energia per unità di area”

o

“L’energia che un’onda trasporta per unità di tempo per unità di area è data dal vettore di Poynting.”

Il vettore di Poynting è rappresentato da Ŝ.

Unità

L’unità SI di Poynting vector è W/m2.

Espressione Matematica

La quantità che viene utilizzato per descrivere la potenza associata con le onde elettromagnetiche è istantanea del vettore di Poynting, che è definita come

$$\hat{S} = \hat{E} \times \hat{H}$$

Dove

• $\hat{S}$ è l’istantanea del vettore di Poynting (W/m2).

• $\hat{E} is è l’intensità istantanea del campo elettrico (V / m).

• $\hat{H} is è l’intensità istantanea del campo magnetico (A / m).

Il punto importante da notare qui è che la grandezza di E è maggiore di H all’interno di un’onda EM. Tuttavia, entrambi contribuiscono con la stessa quantità di energia. Ŝ è il vettore, che ha sia direzione che magnitudine. La direzione di Ŝ è uguale alla velocità dell’onda. La sua grandezza dipende dalla E e H.

Derivazione del vettore di Poynting

Per avere un’idea chiara sul vettore di Poynting, passiamo attraverso la derivazione di questo vettore di Poynting, in un processo passo-passo.

Immaginiamo che un’onda EM, passa un’area (A) perpendicolare all’asse X lungo il quale l’onda viaggia. Mentre passa attraverso A, in tempo infinitesimale (dt), l’onda percorre una distanza (dx).

$$dx = C\ dt$$

Dove

$$C = velocità\ di\ luce = 3\times 10^{8}m/s$$$$volume dv = Adx = AC\ dt$$$$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$$$= \epsilon_{0} AC \ E^{2}\, dt$$

Pertanto, Energia trasferita nel tempo (dt) per area (A) −

$$S = \frac{Energetica}{Tempo\times Area} = \frac{dW}{dt\ A} = \frac{\epsilon_{0}ACE^{2}\, dt}{dt\ A} = \epsilon_{0}C\:E^{2}$$

Dal

$$\frac{E}{H} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \ poi\ S= \frac{CB^{2}}{\mu_{0}}$$

Dal

$$C = \frac{E}{H} \ poi \ S = \frac{EB}{\mu_{0}}$$$$= \hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Ŝ denota il vettore di Poynting.

L’equazione di cui sopra ci dà l’energia per unità di tempo, per unità di area in un dato istante di tempo, che è chiamato come vettore di Poynting.