dove n è il numero di singoli campionati, β = 2 quando la fase gametica è nota e β = 1 se invece la fase non è nota.

Diverse approssimazioni sono utilizzate per dedurre la velocità di ricombinazione usando la distanza fisica (δ) tra due loci come riferimento e traducendola in distanza di collegamento (d), che di solito è descritta come Mb(δ) ≈ cM(d). Per piccoli valori di d quest’ultima approssimazione è valida, ma per valori più grandi di d la probabilità di eventi multipli di ricombinazione e l’interferenza aumenta, inoltre la relazione tra la distanza della mappa e la velocità di ricombinazione non è lineare, poiché la velocità massima di ricombinazione possibile è 0.5. Quindi, a meno che non si usi δ molto breve, l’approssimazione d ≈ c non è ideale (Corbin et al., 2012). Abbiamo quindi implementato funzioni di mappatura per tradurre la d stimata in c, seguendo Haldane (1919), Kosambi (1943), Sved (1971) e Sved e Feldman (1973). Inizialmente SNeP deduce d per ogni coppia di SNP come direttamente proporzionale a δ secondo d = kδ dove k è un valore di velocità di ricombinazione definito dall’utente (il valore predefinito è 10-8 come in Mb = cM). Il valore dedotto di δ può quindi essere sottoposto a una delle funzioni di mappatura disponibili se richiesto dall’utente.

Risolvere l’equazione (3) per Ne e includere tutte le correzioni descritte, consente la previsione di Ne dai dati LD utilizzando (Corbin et al., 2012):

dove Nt è la dimensione effettiva della popolazione t generazioni fa calcolata come t = (2f(ct))-1 (Hayes et al., 2003), ct è la velocità di ricombinazione definita per una specifica distanza fisica tra i marcatori e facoltativamente regolata con le funzioni di mappatura sopra menzionate, r2adj è il valore LD regolato per la dimensione del campione e α:= {1, 2, 2.2} è una correzione per il verificarsi di mutazioni (Ohta e Kimura, 1971). Pertanto, LD su distanze ricombinanti maggiori è informativo sul Ne recente mentre distanze più brevi forniscono informazioni su tempi più lontani nel passato. Un sistema di binning è implementato al fine di ottenere valori medi r2 che riflettono LD per specifiche distanze inter-locus. Il sistema di binning implementato utilizza la seguente formula per definire i valori minimo e massimo per ciascun bin:

Dove bi (ℕ1) è l’i-esimo bin del numero totale di contenitori (totBins), mente, e maxD sono rispettivamente il minimo e il massimo di distanza tra SNPs e x è un numero reale positivo (ℝ0) Quando x è uguale a 1, la distribuzione delle distanze tra i bidoni è lineare e ogni bin ha lo stesso campo di distanza. Per valori più grandi di x la distribuzione delle distanze cambia consentendo un intervallo più ampio sugli ultimi contenitori e un intervallo più piccolo sui primi contenitori. La variazione di questo parametro consente all’utente di avere un numero sufficiente di confronti a coppie per contribuire alla stima Ne finale per ciascun bin.

Esempio di applicazione

Abbiamo testato SNeP con due set di dati pubblicati che erano stati precedentemente utilizzati per descrivere le tendenze in Ne nel tempo utilizzando LD, Bos indicus e Ovis aries . Le stime r2 per i set di dati del bestiame sono state ottenute dagli autori utilizzando GenABLE (Aulchenko et al., 2007) utilizzando una frequenza minima allele (MAF) < 0.01 e regolando la velocità di ricombinazione utilizzando la funzione di mappatura di Haldane (Haldane, 1919). Le stime r2 dei dati sulle pecore sono state calcolate dagli autori usando PLINK-1.07 (Purcell et al., 2007), con MAF < 0.05 e nessuna ulteriore correzione. Per entrambi i set di dati autosomici r2 stima dove corretto per la dimensione del campione utilizzando equazione (4) con β = 2. Per queste analisi comparative la riga di comando SNeP includeva gli stessi parametri utilizzati per i dati pubblicati oltre alle stime r2, calcolate attraverso il conteggio dei genotipi e l’uso della nuova strategia di binning di SNeP.

Risultati

SNeP è un’applicazione multithread sviluppata in C++ e i binari per i più comuni sistemi operativi (Windows, OSX e Linux) possono essere scaricati dahttps://sourceforge.net/projects/snepnetrends/. I binari sono accompagnati da un manuale che descrive l’uso passo-passo di SNeP per dedurre le tendenze in Ne come descritto qui. SNeP produce un file di output con colonne delimitate da tabulazioni che mostrano quanto segue per ogni bin utilizzato per stimare Ne: il numero di generazioni nel passato a cui corrisponde il bin (ad es., 50 generazioni fa), la corrispondente stima Ne, la distanza media tra ogni coppia di SNPs nel bidone, la media r2 e la deviazione standard di r2 nel bidone, e il numero di SNPS utilizzato per calcolare r2 nel bidone. Questo file può essere facilmente importato in Microsoft Excel, R o altri software per tracciare i risultati. I grafici mostrati qui (Figure 1, 3) corrispondono alle colonne di generazioni fa e Ne dal file di output. La colonna con la deviazione standard r2 è fornita per gli utenti di ispezionare la varianza nella stima Ne in ciascun contenitore, in particolare per quei contenitori che riflettono stime temporali più vecchie e che sono meno affidabili in quanto il numero di SNP utilizzati per stimare r2 diventa più piccolo.

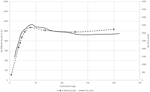
Figura 1. Confronto delle tendenze Ne di sei razze ovine svizzere secondo Burren et al. (2014) (linee tratteggiate) e questo lavoro (linee continue).

Il formato richiesto per i file di input è il formato PLINK standard (file ped e map) (Purcell et al., 2007). SNeP consente agli utenti di calcolare LD sui dati come descritto sopra o utilizzare una matrice LD precalcolata personalizzata per stimare Ne utilizzando l’equazione (5).

L’interfaccia software consente all’utente di controllare tutti i parametri dell’analisi, ad esempio l’intervallo di distanza tra SNPs in bp e l’insieme dei cromosomi utilizzati nell’analisi (ad esempio, 20-23). Inoltre, SNeP include la possibilità di scegliere una soglia MAF (default 0.05), poiché è stato dimostrato che la contabilizzazione della MAF produce stime r2 imparziali indipendentemente dalla dimensione del campione (Sved et al., 2008). L’architettura multithread di SNeP consente il calcolo veloce di grandi set di dati (abbiamo testato fino a ~100K SNPs per un singolo cromosoma), ad esempio i dati BOS descritti qui sono stati analizzati con un processore in 2’43”, l’uso di due processori ha ridotto il tempo a 1’43”, quattro processori hanno ridotto il tempo di analisi a 1’05”.

Esempio Zebu

Per l’analisi zebu, le forme delle curve Ne ottenute con SNeP e le loro tendenze dei dati pubblicati hanno mostrato la stessa traiettoria con un declino regolare fino a circa 150 generazioni fa, seguito da un’espansione con un picco intorno a 40 generazioni fa e termina in un forte declino sulle generazioni più recenti (Figura 1). Tuttavia, mentre le tendenze in entrambe le curve erano le stesse, i due approcci hanno portato a stime Ne diverse, con i valori di SNeP che erano circa tre volte più grandi di quelli nel documento originale. Mentre abbiamo tentato di utilizzare i parametri degli autori nelle nostre analisi, alcune differenze erano inevitabili, cioè la pubblicazione originale dei dati sui bovini stimava r2 con un approccio diverso da quello implementato in SNeP. Le analisi con SNeP erano basate su genotipi, mentre l’analisi originale era basata su inferiti due aplotipi locus, che si traduce nei dati pubblicati che mostrano un r2 atteso di 0.32 alla distanza minima, mentre le nostre stime erano 0.23. Allo stesso modo, Mbole-Kariuki et al. (2014) ottenuto un livello di fondo r2 = 0.013 intorno a 2 Mb, mentre la nostra stima alla stessa distanza era 0.0035 (dati non mostrati). Di conseguenza, poiché le nostre stime di LD erano costantemente più piccole di Mbole-Kariuki et al. (2014) si prevede che le nostre stime Ne dovrebbero essere più grandi. Mentre questa osservazione evidenzia l’importanza di un’attenta scelta dei parametri e delle loro soglie, è importante evidenziare che sebbene la grandezza assoluta dei valori di Ne sia diversa, le tendenze sono quasi identiche.

Esempio di pecore svizzere

Le sei razze ovine svizzere analizzate con SNeP hanno prodotto risultati comparabili con quelli del documento originale (Figura 2), con curve di tendenza per lo più sovrapposte (Figura 3). Tuttavia, la tendenza generale in Ne ha mostrato un declino verso il presente. SNeP ha prodotto valori leggermente più grandi di Ne per il passato più lontano (700-800 generazioni). Ciò è dovuto al diverso sistema di binning utilizzato in SNeP, che consente all’utente di ottenere una distribuzione più uniforme dei confronti a coppie all’interno di ciascun bin (cioè, il numero di SNP confronti a coppie all’interno di ogni bin è comparabile). Per l’arco di tempo che si estende oltre 400 generazioni fa, Burren et al. (2014) ha utilizzato solo tre contenitori nella loro analisi (centrati su 400, 667 e 2000 generazioni fa) mentre per lo stesso intervallo di tempo SNeP ha utilizzato 5 contenitori con un numero di confronti a coppie dipendenti dall’intervallo definito con formule 6a, b. Di conseguenza,l’approccio di Burren e colleghi termina con una maggiore densità di dati che descrivono le generazioni più recenti Pertanto, l’uso di un minor numero di contenitori tende ad aumentare la presenza di valori minori di Ne in ciascun contenitore, riducendo di conseguenza il valore medio di Ne per ciascun contenitore. I valori di Ne per il recente passato, rispetto alla 29a generazione in passato, hanno dato risultati molto simili. La più grande differenza (50) è stata ottenuta per la razza SBS.

Figura 2. Confronto tra i recenti valori Ne calcolati alla 29a generazione in questo lavoro e Burren et al. (2014) per sei razze ovine svizzere.

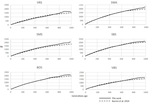
Figura 3. Confronto delle tendenze Ne per le ultime generazioni 250 nei dati SHZ ottenuti da Mbole-Kariuki et al. (2014) (linea tratteggiata) e utilizzando SNeP (linea continua).

Discussione

L’analisi di Ne utilizzando i dati LD è stata dimostrata per la prima volta 40 anni fa, ed è stata applicata, sviluppata e migliorata da allora (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Il numero tradizionalmente ridotto di SNP analizzati non è più una limitazione, poiché i chip SNP comprendono un numero estremamente elevato di SNP, disponibili in breve tempo e ad un prezzo ragionevole. Ciò ha potenziato l’uso del metodo, che è stato applicato agli esseri umani (Tenesa et al., 2007; McEvoy et al., 2011) nonché a diverse specie addomesticate (England et al., 2006; Uimari e Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Insieme a questi miglioramenti, i limiti metodologici sono diventati evidenti e sono stati affrontati qui, con la maggior parte degli sforzi che puntano alla corretta stima del recente Ne. Tuttavia, il valore quantitativo della stima dipende fortemente dalla dimensione del campione, dal tipo di stima LD e dal processo di binning (Waples e Do, 2008; Corbin et al., 2012), mentre il suo modello qualitativo dipende più dall’informazione genetica che dalla manipolazione dei dati.

Finora questo metodo è stato applicato utilizzando una varietà di software, non esiste un approccio standardizzato per binare i risultati e ogni studio ha applicato un approccio più o meno arbitrario, ad esempio, binning per le classi di generazione in passato (Corbin et al., 2012), binning per classi di distanza con un intervallo costante per ogni bin (Kijas et al., 2012) o binning per classi di distanza in modo lineare ma con bidoni più grandi per i punti temporali più recenti (Burren et al., 2014). A nostra conoscenza l’unico software disponibile che stima Ne attraverso LD è NeEstimator (Do et al., 2014), una versione aggiornata del precedente LDNE (Waples e Do, 2008) che consente l’analisi di un set di dati di grandi dimensioni (come 50k SNPChip). È importante sottolineare che, mentre SNeP si concentra sulla stima delle tendenze Ne storiche, l’obiettivo di NeEstimator è quello di produrre stime Ne imparziali contemporanee, quest’ultima dovrebbe quindi essere considerata come uno strumento complementare mentre indaga la demografia attraverso LD.

Abbiamo utilizzato SNeP per analizzare due set di dati in cui il metodo è stato precedentemente applicato. I risultati ottenuti per i dati sulle pecore sono stati sia quantitativamente che qualitativamente comparabili con quelli ottenuti da Burren et al. (2014), mentre per i dati Zebu abbiamo ottenuto una stima della tendenza Ne che corrispondeva strettamente a quella di Mbole-Kariuki et al. (2014) sebbene le nostre stime puntuali di Ne fossero più grandi di quelle descritte per i dati (Mbole-Kariuki et al., 2014). La discrepanza tra questi due risultati riflette che Burren e colleghi hanno prodotto le loro stime r2 utilizzando PLINK (il software standard per la manipolazione dei dati SNP su larga scala) che utilizza lo stesso approccio utilizzato per stimare r2 da SNeP, mentre Mbole-Kariuki et al. seguito Hao et al. (2007) per la stima r2. L’uso di stime diverse per LD è fondamentale per l’aspetto quantitativo della curva Ne, dove a causa della correlazione iperbolica tra Ne e r2, una diminuzione di r2 sul suo intervallo più vicino a 0 può portare a un cambiamento molto grande nelle stime Ne, mentre le differenze nelle stime sono meno significative quando il valore di r2 è alto, cioè più vicino a 1. Pertanto, sebbene in uno dei set di dati i valori Ne fossero sostanzialmente diversi, in entrambi i casi le curve Ne si sovrapponevano a quelle originariamente pubblicate.

Come già suggerito da altri autori, l’affidabilità delle stime quantitative ottenute con questo metodo deve essere presa con cautela, soprattutto per i valori di Ne relativi alle generazioni più recenti e più antiche (Corbin et al., 2012) perché per le generazioni recenti sono coinvolti grandi valori di c, non adattando le implicazioni teoriche che Hayes ha proposto di stimare una variabile Ne nel tempo (Hayes et al., 2003). Le stime per le generazioni più vecchie potrebbero anche essere inaffidabili in quanto la teoria coalescente mostra che nessun SNP può essere campionato in modo affidabile dopo le generazioni 4Ne in passato (Corbin et al., 2012). Inoltre, le stime Ne, e in particolare quelle relative alle generazioni successive, sono fortemente influenzate da fattori di manipolazione dei dati, come la scelta dei valori MAF e alfa. Inoltre, la strategia di binning applicata può interferire con la precisione generale del metodo, ad esempio quando viene utilizzato un numero insufficiente di confronti a coppie per popolare ciascun bin.

Una delle applicazioni del metodo è quella di confrontare le demografie di razza. In questo caso la forma delle curve Ne sarebbe lo strumento ottimale per differenziare diverse storie demografiche, più dei loro valori numerici, usandole come potenziale impronta demografica per quella razza o specie, tenendo tuttavia in considerazione che la mutazione, la migrazione e la selezione possono influenzare la stima Ne attraverso LD (Waples e Do, 2010). Inoltre, un’attenta considerazione dei dati analizzati con SNeP (e altri software per stimare Ne) è molto importante, in quanto la presenza di fattori confondenti come la mescolanza, può comportare stime distorte di Ne (Orozco-terWengel e Bruford, 2014).

L’obiettivo di SNeP è quindi quello di fornire uno strumento veloce e affidabile per applicare metodi LD per stimare Ne utilizzando dati genotipici ad alto throughput in modo più coerente. Consente due diversi approcci di stima r2 più la possibilità di utilizzare stime r2 da software esterno. L’uso di SNeP non supera i limiti del metodo e della teoria dietro di esso, ma consente all’utente di applicare la teoria utilizzando tutte le correzioni suggerite fino ad oggi.

Contributi dell’autore

MB ha ideato e scritto il software e il manoscritto. MB, MT e POtW hanno testato il software ed eseguito le analisi. MT, POtW, e MWB rivisto il manoscritto. Tutti gli autori hanno approvato il manoscritto finale.

Dichiarazione sul conflitto di interessi

Gli autori dichiarano che la ricerca è stata condotta in assenza di relazioni commerciali o finanziarie che potrebbero essere interpretate come un potenziale conflitto di interessi.

Ringraziamenti

Ringraziamo Christine Flury per aver fornito i dati sulle pecore e per una discussione utile. Ringraziamo anche i due revisori per i suggerimenti utili per migliorare questo documento. MB è stato supportato dal programma Master and Back (Regione Sardegna).