Filtri Kalman

L’algoritmo utilizzato per unire i dati è chiamato filtro Kalman.

Il filtro Kalman è uno degli algoritmi più diffusi nella fusione dei dati. Inventato nel 1960 da Rudolph Kalman, è ora utilizzato nei nostri telefoni o satelliti per la navigazione e il monitoraggio. L’uso più famoso del filtro fu durante la missione Apollo 11 per inviare e riportare l’equipaggio sulla luna.

Quando usare un filtro Kalman ?

Un filtro Kalman può essere utilizzato per la fusione dei dati per stimare lo stato di un sistema dinamico (in evoluzione nel tempo) nel presente (filtraggio), nel passato (livellamento) o nel futuro (previsione). I sensori incorporati nei veicoli autonomi emettono misure a volte incomplete e rumorose. L’imprecisione dei sensori (rumore) è un problema molto importante e può essere gestito dai filtri Kalman.

Un filtro Kalman viene utilizzato per stimare lo stato di un sistema, indicato con x. Questo vettore è composto da una posizione p e una velocità v.

Ad ogni stima, associare una misura di incertezza P.

esecuzione di una fusione di sensori, prendiamo in considerazione i dati diversi per lo stesso oggetto. Un radar può stimare che un pedone è a 10 metri di distanza, mentre il Lidar stima che sia a 12 metri. L’utilizzo dei filtri Kalman permette di avere un’idea precisa per decidere quanti metri realmente è il pedone eliminando il rumore dei due sensori.

Un filtro Kalman può generare stime dello stato degli oggetti che lo circondano. Per fare una stima, sono necessarie solo le osservazioni attuali e la previsione precedente. La cronologia delle misurazioni non è necessaria. Questo strumento è quindi leggero e migliora con il tempo.

Come appare

Lo stato e l’incertezza sono rappresentati dai Gaussiani.

Una Gaussiana è una funzione continua in cui la zona è 1. Questo ci permette di rappresentare le probabilità. Siamo su una probabilità di distribuzione normale. L’uni-modalità dei filtri Kalman significa che abbiamo un singolo picco ogni volta per stimare lo stato del sistema.

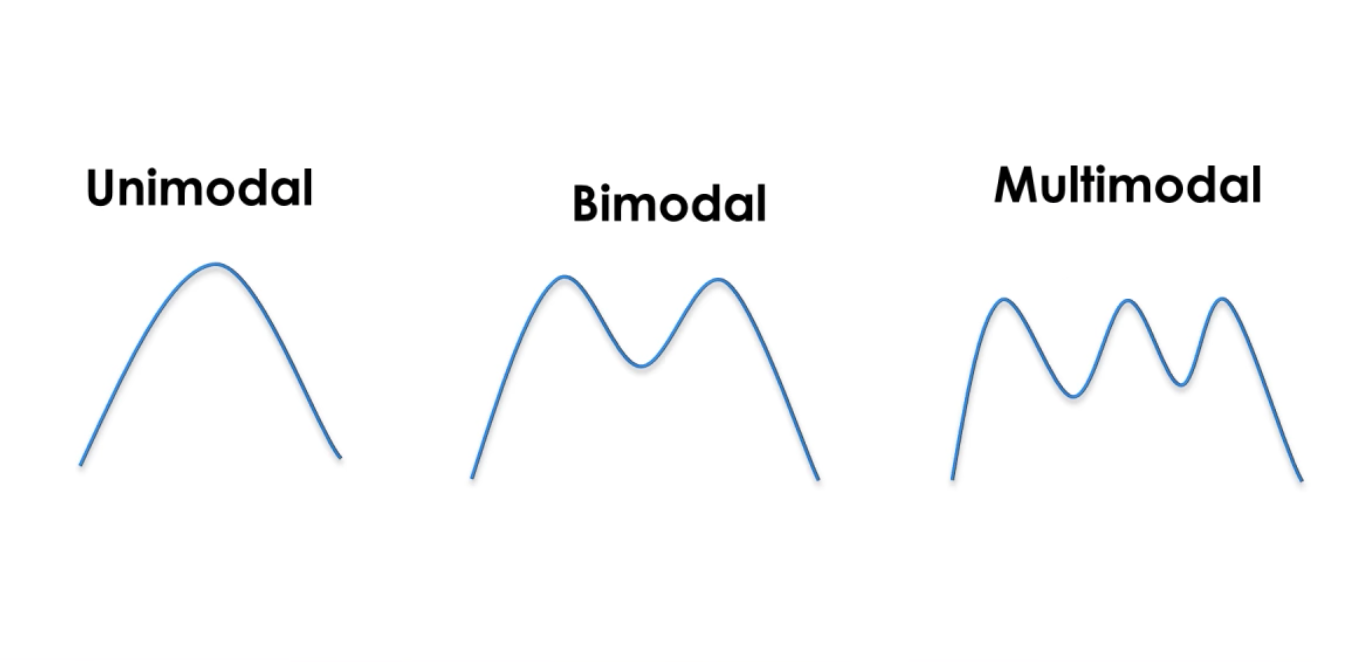
Abbiamo una media µ rappresenta uno stato e una varianza σ2, che rappresenta un’incertezza. Maggiore è la varianza, maggiore è l’incertezza.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Usiamo le osservazioni dei nostri sensori per correggere lo stato previsto e ottenere una stima più accurata.

Per fare una stima, un filtro Kalman richiede solo le osservazioni correnti e la previsione precedente. La cronologia delle misurazioni non è necessaria.

Matematica

La matematica dietro i filtri Kalman è fatta di aggiunte e moltiplicazioni di matrici. Abbiamo due fasi: Previsione e aggiornamento.

Previsione
La nostra previsione consiste nel stimare uno stato x’ e un’incertezza P’ al tempo t dagli stati precedenti x e P al tempo t-1.

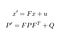
• F: Matrice di transizione da t-1 a t
• ν: Rumore aggiunto
• Q: La matrice di covarianza tra cui il rumore

Aggiornamento
La fase di aggiornamento consiste nell’utilizzo di un z misura da un sensore di correggere la nostra stima e quindi prevedere x e P.

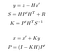
• y: Differenza tra la misura attuale e di previsione, cioè l’errore.
• S: Errore di sistema stimato
• H: Matrice di transizione tra il marcatore del sensore e il nostro.
• R: Matrice di covarianza relativa al rumore del sensore (data dal produttore del sensore).
• K: Guadagno di Kalman. Coefficiente tra 0 e 1 che riflette la necessità di correggere la nostra previsione.

La fase di aggiornamento consente di stimare una x e una P più vicine alla realtà di quanto le misurazioni forniscano.

Un filtro Kalman consente previsioni in tempo reale, senza dati in anticipo. Usiamo un modello matematico basato sulla moltiplicazione di matrici per ogni volta che definisce uno stato x (posizione, velocità) e incertezza P.

Ristampa Prior/Posterior

Questo diagramma mostra cosa succede in un filtro Kalman.

• stato stimato stima rappresenta la nostra prima stima, la nostra previsione di fase. Stiamo parlando di prior.
• La misura è la misura da uno dei nostri sensori. Abbiamo una migliore incertezza, ma il rumore dei sensori lo rende una misura che è sempre difficile da stimare. Parliamo di verosimiglianza.
• La stima dello stato ottimale è la nostra fase di aggiornamento. L’incertezza è questa volta la più debole, abbiamo accumulato informazioni e permesso di generare un valore più sicuro che con il nostro solo sensore. Questo valore è la nostra ipotesi migliore. Parliamo di posteriore.

Ciò che un filtro Kalman implementa è in realtà una regola di Bayes.

In un filtro di Kalman, siamo in loop le previsioni di misurazioni. Le nostre previsioni sono sempre più precise poiché manteniamo una misura di incertezza e calcoliamo regolarmente l’errore tra la nostra previsione e la realtà. Siamo in grado dalle moltiplicazioni delle matrici e dalle formule di probabilità di stimare le velocità e le posizioni dei veicoli intorno a noi.

Filtri”Extended / Unscented” e non linearità

Si pone un problema essenziale. Le nostre formule matematiche sono tutte implementate con funzioni lineari di tipo y = ax + b.
Un filtro Kalman funziona sempre con funzioni lineari. D’altra parte, quando usiamo un Radar, i dati non sono lineari.

Il Radar vede il mondo con tre misure:

Questi tre valori rendono la nostra misurazione non lineare data l’inclusione dell’angolo φ.

Il nostro obiettivo qui è convertire i dati ρ, φ, ρ in dati cartesiani (px, py, vx, vy).

Se inseriamo dati non lineari in un filtro Kalman, il nostro risultato non è più in forma gaussiana uni-modale e non possiamo più stimare posizione e velocità.

abbiamo Quindi utilizzare approssimazioni, che è il motivo per cui stiamo lavorando su due metodi:
– filtri di Kalman Esteso uso Jacobiano e serie di Taylor per linearizzare il modello.
– I filtri Kalman inodore utilizzano un’approssimazione più precisa per linearizzare il modello.

Per affrontare l’inclusione della non linearità da parte del Radar, esistono tecniche che permettono ai nostri filtri di stimare la posizione e la velocità degli oggetti che vogliamo tracciare.