In alcune circostanze, la corrente nell’avvolgimento di un induttore toroidale contribuisce solo al campo B all’interno degli avvolgimenti e non contribuisce al campo B magnetico all’esterno degli avvolgimenti. Questa è una conseguenza della simmetria e della legge circuitale di Ampère.

condizioni Sufficienti per un totale interno di confinamento del B fieldEdit

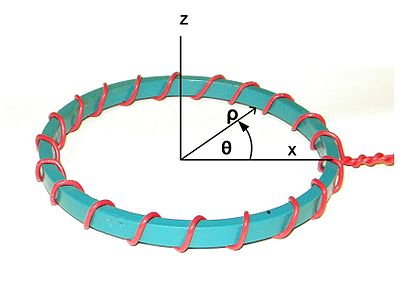Fig. 1. Sistema di coordinate. L’asse Z è l’asse nominale di simmetria. L’asse X scelto arbitrariamente per allinearsi con il punto di partenza dell’avvolgimento. ρ è chiamato direzione radiale. θ è chiamata la direzione circonferenziale.

Fig. 2. Un induttore toroidale assialmente simmetrico senza corrente circonferenziale.

L’assenza di circonferenziale corrente (il percorso della circonferenza corrente è indicato dalla freccia rossa nella figura 3 di questa sezione) e il assialmente disposizione simmetrica dei conduttori e materiali magnetici sono condizioni sufficienti per un totale interno di confinamento del campo B. (Alcuni autori preferiscono usare il campo H). A causa della simmetria, le linee del flusso B devono formare cerchi di intensità costante centrati sull’asse di simmetria. Le uniche linee di flusso B che circondano qualsiasi corrente sono quelle che si trovano all’interno dell’avvolgimento toroidale. Pertanto, dalla legge circuitale di Ampere, l’intensità del campo B deve essere zero al di fuori degli avvolgimenti.

Fig. 3. Induttore toroidale con corrente circonferenziale

La figura 3 di questa sezione mostra l’avvolgimento toroidale più comune. Fallisce entrambi i requisiti per il confinamento totale del campo B. Guardando fuori dall’asse, a volte l’avvolgimento si trova all’interno del nucleo e talvolta si trova all’esterno del nucleo. Non è assialmente simmetrico nella regione vicina. Tuttavia, in punti una distanza di diverse volte la spaziatura di avvolgimento, il toroide sembra simmetrico. C’è ancora il problema della corrente circonferenziale. Non importa quante volte l’avvolgimento circonda il nucleo e non importa quanto sia sottile il filo, questo induttore toroidale includerà ancora un anello di una bobina nel piano del toroide. Questo avvolgimento produrrà anche e sarà suscettibile di un campo E nel piano dell’induttore.

Le figure 4-6 mostrano diversi modi per neutralizzare la corrente circonferenziale. La figura 4 è la più semplice e ha il vantaggio che il filo di ritorno può essere aggiunto dopo che l’induttore è stato acquistato o costruito.

Fig. 4. Corrente circonferenziale contrastata con un filo di ritorno. Il filo è bianco e corre tra il bordo esterno dell’induttore e la parte esterna dell’avvolgimento.

Fig. 5. Corrente circonferenziale contrastata con un avvolgimento di ritorno.

Fig. 6. Corrente circonferenziale contrastata con un avvolgimento di ritorno diviso.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

Ci sarà una distribuzione di potenziale lungo l’avvolgimento. Questo può portare ad un campo E nel piano del toroide e anche una suscettibilità ad un campo E nel piano del toroide come mostrato in figura 7. Questo può essere mitigato utilizzando un avvolgimento di ritorno come mostrato in figura 8. Con questo avvolgimento, ogni luogo l’avvolgimento si attraversa, le due parti saranno a polarità uguale e opposta che riduce sostanzialmente il campo E generato nel piano.

Induttore/trasformatore toroidale e potenziale vettoriale magneticomodifica

Mostrando lo sviluppo del potenziale vettoriale magnetico attorno a un induttore toroidale simmetrico.

Vedi Feynman capitolo 14 e 15 per una discussione generale del potenziale vettoriale magnetico. Vedi Feynman pagina 15-11 per un diagramma del potenziale vettoriale magnetico attorno a un solenoide lungo e sottile che presenta anche un confinamento interno totale del campo B, almeno nel limite infinito.

Il campo A è accurato quando si utilizza l’ipotesi b f A = 0 {\displaystyle bf{A}=0}

. Questo sarebbe vero sotto le seguenti ipotesi:

• 1. il calibro di Coulomb è usato
• 2. viene utilizzato il misuratore di Lorenz e non c’è distribuzione di carica, ρ = 0 {\displaystyle \rho =0\,}
  
• 3. viene utilizzato il calibro di Lorenz e si assume la frequenza zero
• 4. viene utilizzato l’indicatore di Lorenz e viene assunta una frequenza diversa da zero abbastanza bassa da trascurare 1 c 2 t t {\displaystyle {\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}}
  

  .

Il numero 4 sarà presunto per il resto di questa sezione e può essere riferito alla “condizione quasi statica”.

Sebbene l’induttore toroidale assialmente simmetrico senza corrente circonferenziale limiti totalmente il campo B all’interno degli avvolgimenti, il campo A (potenziale vettoriale magnetico) non è limitato. La freccia # 1 nell’immagine raffigura il potenziale vettoriale sull’asse di simmetria. Le sezioni di corrente radiale a e b sono distanze uguali dall’asse ma puntate in direzioni opposte, quindi si annulleranno. Allo stesso modo i segmenti c e d annullano. In effetti tutti i segmenti di corrente radiale si annullano. La situazione per le correnti assiali è diversa. La corrente assiale all’esterno del toroide è puntata verso il basso e la corrente assiale all’interno del toroide è puntata verso l’alto. Ogni segmento di corrente assiale all’esterno del toroide può essere abbinato a un segmento uguale ma diretto in modo opposto all’interno del toroide. I segmenti all’interno sono più vicini dei segmenti all’esterno all’asse, quindi c’è una componente netta verso l’alto del campo A lungo l’asse di simmetria.

che Rappresenta il magnetico vettore potenziale (A), flusso magnetico (B) e densità di corrente (j) campi intorno a un induttore toroidale di sezione circolare. Linee più spesse indicano linee di campo di intensità media superiore. I cerchi nella sezione trasversale del nucleo rappresentano il flusso B che esce dall’immagine. I segni più sull’altra sezione trasversale del nucleo rappresentano il flusso B che entra nell’immagine. Div A = 0 è stato assunto.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ t → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

) hanno la stessa forma, le linee e i contorni di Un relazionarsi B come le linee e i contorni di B si riferiscono a j. Così, una raffigurazione di Un campo intorno a un ciclo di B flusso (come sarebbe prodotta in un induttore toroidale) è qualitativamente la stessa come il campo B intorno a un loop di corrente. La figura a sinistra è la rappresentazione di un artista del campo A attorno a un induttore toroidale. Le linee più spesse indicano percorsi di intensità media superiore (i percorsi più brevi hanno un’intensità maggiore in modo che l’integrale del percorso sia lo stesso). Le linee sono appena disegnate per guardare bene e impartire aspetto generale del campo A.

Azione del trasformatore toroidale in presenza di confinamento totale del campo Bedit

I campi E e B possono essere calcolati dai campi A e {{\displaystyle \phi\,}

(potenziale elettrico scalare) B = × × A . {\displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {A} .}

e : E = − ∇ ϕ − ∂ A ∂ t {\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}

e quindi, anche se la regione al di fuori degli avvolgimenti è privo di campo B, è riempito con i non-zero E campo. La quantità ∂ A ∂ t {\displaystyle {\frac {\partial \mathbf {A} }{\partial t}}}

è responsabile per l’auspicabile campo magnetico di accoppiamento tra primario e secondario, mentre la quantità ∇ ϕ {\displaystyle \nabla \phi \,}

è responsabile per l’indesiderabile campo elettrico accoppiamento tra primario e secondario. I progettisti di trasformatori tentano di ridurre al minimo l’accoppiamento del campo elettrico. Per il resto di questa sezione, unless {\displaystyle \nabla \phi \,}

sarà assunto come zero se non diversamente specificato.

Si applica il teorema di Stokes, in modo che l’integrale di percorso di A sia uguale al flusso B chiuso, proprio come l’integrale di percorso B è uguale a una costante volte la corrente chiusa

L’integrale di percorso di E lungo l’avvolgimento secondario dà l’EMF indotta del secondario (forza elettro-Motrice).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

che dice che il EMF è uguale al tempo tasso di cambio del B flusso racchiuso da una tortuosa, che è il risultato di consueto.

trasformatore Toroidale vettore di Poynting giunto dalla scuola primaria alla secondaria in presenza di totale B campo confinementEdit

In questa figura, punti blu indicano dove B flusso primario di corrente viene fuori l’immagine e il segno più indica dove va in scena.

Spiegazione della figuraEdit

Questa figura mostra la mezza sezione di un trasformatore toroidale. Si assumono condizioni quasi statiche, quindi la fase di ciascun campo è ovunque la stessa. Il trasformatore, i suoi avvolgimenti e tutte le cose sono distribuiti simmetricamente sull’asse di simmetria. Gli avvolgimenti sono tali che non c’è corrente circonferenziale. I requisiti sono soddisfatti per il confinamento interno completo del campo B a causa della corrente primaria. Il nucleo e l’avvolgimento primario sono rappresentati dal toro grigio-marrone. L’avvolgimento primario non viene mostrato, ma la corrente nell’avvolgimento sulla superficie della sezione trasversale viene mostrata come ellissi dorate (o arancioni). Il campo B causato dalla corrente primaria è interamente confinato nella regione racchiusa dall’avvolgimento primario (cioè il nucleo). I punti blu sulla sezione trasversale della mano sinistra indicano che le linee di flusso B nel nucleo escono dalla sezione trasversale della mano sinistra. Sull’altra sezione trasversale, i segni blu più indicano che il flusso B entra lì. Il campo E proveniente dalle correnti primarie è mostrato come ellissi verdi. L’avvolgimento secondario è mostrato come una linea marrone che scende direttamente lungo l’asse di simmetria. Nella pratica normale, le due estremità del secondario sono collegate tra loro con un lungo filo che rimane ben lontano dal toro, ma per mantenere l’assoluta simmetria assiale, l’intero apparato è immaginato come all’interno di una sfera perfettamente conduttiva con il filo secondario “collegato” all’interno della sfera a ciascuna estremità. Il secondario è fatto di filo di resistenza, quindi non c’è carico separato. Il campo E lungo il secondario causa corrente nel secondario (frecce gialle) che causa un campo B attorno al secondario (mostrato come ellissi blu). Questo campo B riempie lo spazio, incluso all’interno del nucleo del trasformatore, quindi alla fine, c’è un campo B continuo diverso da zero dal primario al secondario, se il secondario non è aperto in circuito. Il prodotto incrociato del campo E (proveniente dalle correnti primarie) e del campo B (proveniente dalle correnti secondarie) forma il vettore di Poynting che punta dal primario verso il secondario.