Hehe He Ci è stato insegnato a moltiplicare su e giù per il coniugato del denominatore. Questo coniugato è ottenuto sostituendo $-$ da $+$ (o viceversa) al denominatore:

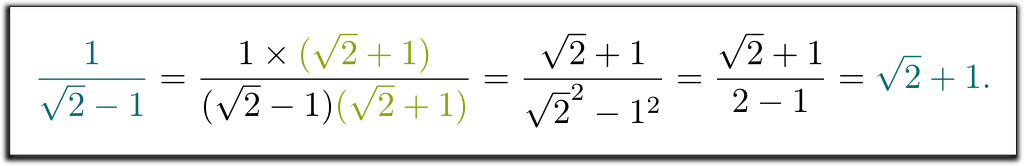
Lo so! L’espressione complicata $1 / (\sqrt{2}-1) represents rappresenta lo stesso numero di$ \sqrt{2}+1$. E questo spiega perché i nostri insegnanti volevano che scrivessimo i risultati in un modo piuttosto che nell’altro: quando tutto è scritto nello stesso modo, gli esami diventano molto più facili da correggere!

Ma che dire di $1 / (\sqrt{2}-1)$? Puoi sbarazzarti della radice nel denominatore? Si può anche fare?

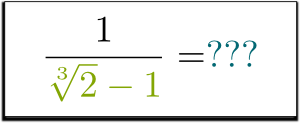
Lo so!

Dimmelo tu!

Hai avuto fortuna?

Hehe Interestingly È interessante notare che qualsiasi potenza di \ \ sqrt{2}-1 can può essere scritta come somma di potenze di powers\sqrt{2}$. In effetti, devi solo distribuire i prodotti:

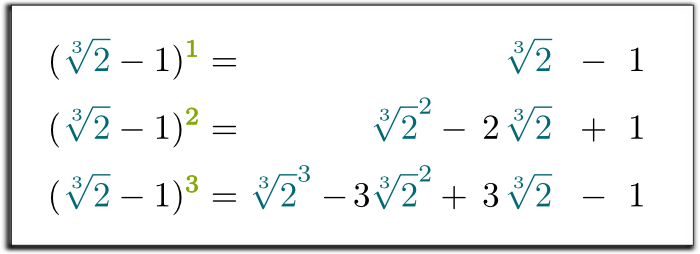
Sì, lo è! Facendo questa sostituzione nella terza equazione, abbiamo dimostrato che le prime tre potenze di $\sqrt{2}-1$ può essere scritto come somma di un numero razionale, di $\sqrt{2}$ e di $\sqrt{2}^2$!

Quindi ora abbiamo 3 equazioni, con 2 espressioni radice che vogliamo eliminare! Quindi, possiamo combinare le equazioni per rimuovere tutte le espressioni radice sulla destra!

Moltiplichiamo le 2 prime righe per 3 e sommiamo tutte e 3 le equazioni:

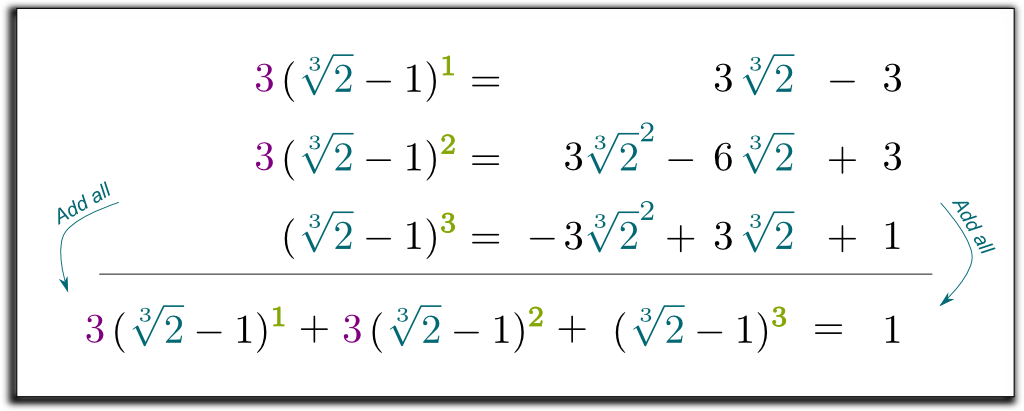
Hehe He La cosa interessante è che il termine sinistro che abbiamo ottenuto può ora essere fattorizzato da \ \ sqrt{2} -1!! Lasciatemi saltare alcuni calcoli noiosi And E arrivare al risultato ((\sqrt{2}-1) \ (\sqrt {2} ^ 2 + \ sqrt{2} + 1)$ $= 1$. Quindi, per eliminare le radici nel denominatore, possiamo moltiplicare su e giù per \ \ sqrt{2}^2 + \sqrt{2} + 1!! Infine, otteniamo la seguente formula sorprendente e bella:

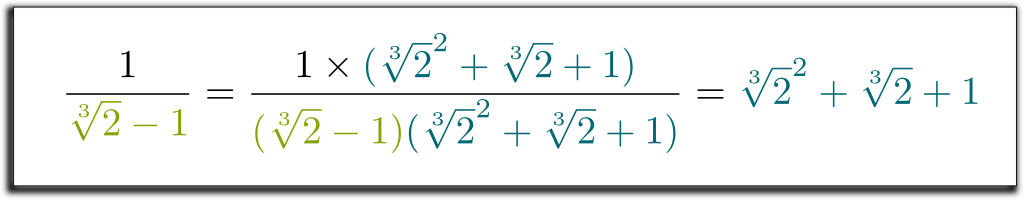
Lo so! Ma ciò che è ancora più ordinato è che il metodo che abbiamo usato è molto generale! Con tecniche simili, ora possiamo rimuovere tutti i radicali dai denominatori!

Ora, ciò che era di particolare interesse per Galois non era il fatto che un metodo consentisse di rimuovere i radicali dai denominatori. Ma piuttosto, che qualsiasi numero con radicali in denominatori eguagliava un numero con radicali in cima. Ciò significava che i numeri con i radicali in cima erano stabili per divisione.

È comune indicare $\mathbb Q{2}] the l’insieme di numeri che possono essere scritti come somma di potenze di \ \ sqrt{2}$. Dato che $\sqrt{2}^3 = 2$ è un numero razionale, qualsiasi somma di potenze di $\sqrt{2}$, infatti, può essere scritto nella forma standard $a\sqrt{2}^2 + b\sqrt{2} + c$. Ora, se aggiungi, sottrai o moltiplichi due numeri di questo tipo, non è difficile vedere che otteniamo numeri che possono ancora essere messi nella forma standard a a\sqrt{2}^2 + b\sqrt{2} + c$. Inoltre, quello che abbiamo appena mostrato qui è che l’inverso di tutti i numeri can a\sqrt{2}^2 + b\sqrt{2} + c can può anche essere scritto in forma standard. Questo dimostra che ogni addizione, sottrazione, moltiplicazione e divisione di numeri in math\mathbb Q{2}] yields produce un numero, che può essere scritto in forma standard belongs e quindi appartiene a belongs\mathbb Q{2}]$. In termini di algebra pura, $ \ mathbb Q {2}]$ è quindi stabile dalle quattro operazioni aritmetiche classiche. Per questo motivo, lo chiamiamo un campo.

Geometria delle estensioni di campo

Il campo con cui hai più familiarità è probabilmente l’insieme math\mathbb Q of dei numeri razionali. Altri esempi di campi sono gli insiemi R \ mathbb R of di numeri reali e l’insieme C \ mathbb C C di numeri complessi. E ora, abbiamo anche math \ mathbb Q{2}]$. Poiché $\mathbb Q{2}]$ è un campo che contiene il campo $\mathbb Q$, diciamo che $\mathbb Q{2}] / \mathbb Q$ è un campo di estensione.

Il fatto che $\mathbb Q{2}] / \mathbb Q is sia un’estensione di campo produce una connessione molto naturale tra i due campi. Vale a dire, $\mathbb Q{2}]$ può essere visto come uno spazio vettoriale, dove \ \ mathbb Q is è il campo scalare. In particolare, il fatto che un qualsiasi numero in $\mathbb Q{2}]$ può essere scritto $a \sqrt{2}^2 + b\sqrt{2} + c$ significa che $(1, \sqrt{2}, \sqrt{2}^2)$ costituisce una base di $\mathbb Q{2}]$ come $\mathbb Q$-spazio vettoriale. E questo significa che possiamo rappresentarlo geometricamente come uno spazio a 3 dimensioni!

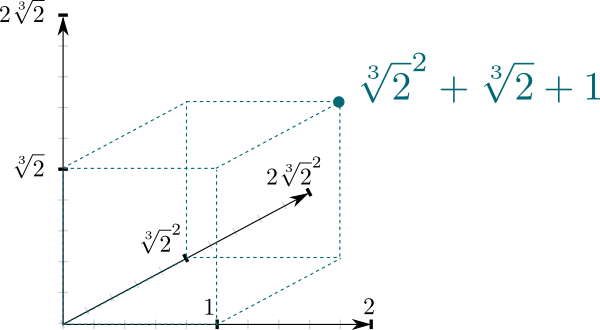
La dimensione dello spazio vettoriale sopra è una proprietà interessante delle estensioni di campo. È conosciuto come il grado, ed è comunemente indicato $ \ big{2}]: \ mathbb Q \ big] = 3.per esempio.

Sì! In realtà è abbastanza facile creare un’estensione di campo di questo: basta aggiungere un numero radicale che non appartiene a math\mathbb Q{2}]!!

Sì! Questo creerebbe il campo $(\mathbb Q {2}]) = \ mathbb Q {2},\sqrt{2}]$. Questi campi contengono tutti i numeri che sono prodotti e somme di $\sqrt{2} and e $\sqrt{2}$. Questi sono della forma $a\sqrt{2}^2$+$b\sqrt{2}+c$+$ d\sqrt{2}^2\sqrt{2}$ +$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2}$. Qualche idea di quale sia il grado degree \ big{2}, \ sqrt{2}]: \mathbb Q{2}]\big] is?

Sì! Infatti, abbiamo $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} \sqrt{2} $+$ f \sqrt{2} $=$ (a\sqrt{2}^2+b\sqrt{2}+c) $ + $d\sqrt{2}^2 + b \sqrt{2} + f) \sqrt{2}$. Così, un numero qualsiasi di $\mathbb Q{2},\sqrt{2}]$ può essere scritto $A+B\sqrt{2}$, dove $A$ e $B$ appartiene a $\mathbb Q{2}]$. Quindi, 2 scalari di math \ mathbb Q {2}] determine determinano un numero in $\mathbb Q{2},\sqrt{2}]$. Ciò significa che il grado dell’estensione del campo $\mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}] is è 2. Infatti, abbiamo la relazione Chasles \ \ big{2}, \ sqrt{2}]: \ mathbb Q \ big] = = big \ big{2}, \sqrt{2}] : \ mathbb Q {2}] \ big] \ big{2}]: \ mathbb Q \ big] $ = times 2 \ volte 3 = 6$.

È meglio di così! Qualsiasi estensione di campo di grado finito, chiamata estensione di campo finito, è attraversata da un singolo numero. Per esempio $\mathbb Q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, il che significa che tutti i numeri che sono somme di potenze di $\sqrt{2}$ e $\sqrt{2}$ sono anche somme di potenze di $\sqrt{2} + \sqrt{2}$. Non è sorprendentemente fantastico?

Più in generale, qualsiasi finiti campo di estensione di $\mathbb Q$ può essere scritto $\mathbb Q$ alcuni $x$, che viene aggiunto a $\mathbb Q$.

Sì. È il caso dell’estensione del campo \ \ mathbb R / \ mathbb Q$. E, così è l’estensione di campo più importante nella teoria di Galois! Questa estensione del campo è $ \ bar {\mathbb Q} / \ mathbb Q$, dove $ \ bar {\mathbb Q} is è l’insieme dei numeri algebrici. Queste sono tutte soluzioni alle equazioni polinomiali della forma a a_n x ^ n + + {a_ {n-1} x ^ {n-1} $+$ … $+$ a_1 x + + a a_0 = 0$. Ad esempio, $\sqrt{2}$ è un numero algebrico perché è la soluzione a x x^4 – 2x = 0.. Quindi, $ \ bar {\mathbb Q}$ è un’estensione di campo per tutte le estensioni di campo finite di Q \ mathbb Q$.

Numeri coniugati

Siamo quasi arrivati! Abbiamo bisogno di una deviazione finale attraverso equazioni polinomiali.

Esattamente! Galois notò che alcune equazioni potevano essere semplificate. Per esempio, $x^4-2x=0$ può essere factorized come $x(x^3-2)=0$, che corrisponde a $x=0$ o $x^3-2=0$. Così, l’equazione $x^4-2x=0$ può essere ridotto a equazioni $x=0$ e $x^3-2=0$. E infatti, questa riduzione è molto simile a come numeri come 35 possono essere ridotti a 5 e 7, perché 5 5 \ per 7 = 35$. La somiglianza tra equazioni e numeri interi è così forte che possiamo persino creare divisioni euclidee di polinomi, proprio come hai imparato a farlo per i numeri! A destra c’è un esempio di tale divisione (non preoccuparti se non lo capisci, non sarà importante per il sequel).

! Queste sono note come equazioni polinomiali irriducibili. L’equazione x x^3-2=0 is è un esempio di equazione polinomiale irriducibile.

Sì! Ma, in modo cruciale, Galois voleva concentrarsi sulle equazioni con coefficienti razionali. O, meglio, polinomi con coefficienti che appartengono al campo base. Quindi, quello che intendevo era che, per math \ mathbb Q as come campo base, x x^3-2=0 is è irriducibile.

Consideriamo x x^2 – 2x -1=0 to per avere alcuni indizi. Questa equazione può essere dimostrata irriducibile. Ti ricordi come risolverlo?

Se b b^2-4ac \ geq 0 yes, sì.

Esattamente! Così, il polinomio irriducibile di equazione $x^2 + 2x -1=0$ ha due soluzioni: $1+\sqrt{2}$ e $1-\sqrt{2}$… nessun commento?

Bingo! Questa è la scoperta chiave di Galois. Più in generale, Galois chiamato coniuga tutte le soluzioni di un’equazione polinomiale irriducibile. E, come potete immaginare, questi sono essenziali per rimuovere i radicali dai denominatori!

La prima cosa da notare è che, se $x_1$, $x_2$, …, $x_n$ sono tutte le soluzioni di un polinomio irriducibile di equazione $a_n x^n + a_{n-1} x^{n-1} $+$ … + a_1 x + a_0 = 0$ con coefficienti razionali, quindi questo polinomio irriducibile equazione può effettivamente essere riscritto $a_n(x-x_1)(x-x_2)…(x-x_n)=0$. L’identificazione dei termini costanti produce quindi yields x_1 x_2 x x_n = = ((-1)^n a_0 / a_n.. Quindi, in modo cruciale, il prodotto dei numeri coniugati è il numero razionale number(-1)^n a_0/a_n$, che è diverso da zero (dimostralo!).

Ecco un piccolo scherzo da tenere a mente la forte connessione tra coniugati:

Considera una frazione fraction 1 / x_1 where, dove x x_1 is è un’espressione complicata con radicali. Moltiplicando su e giù dai coniugati $x_2$, …, $x_n$ di $x_1$, poi, cede $1/x_1 $=$ (-1)^n a_n x_2…x_n/a_0$, che non ha alcun radicale al denominatore come abbiamo stabilito $a_0$ per essere un numero diverso da zero del campo base!

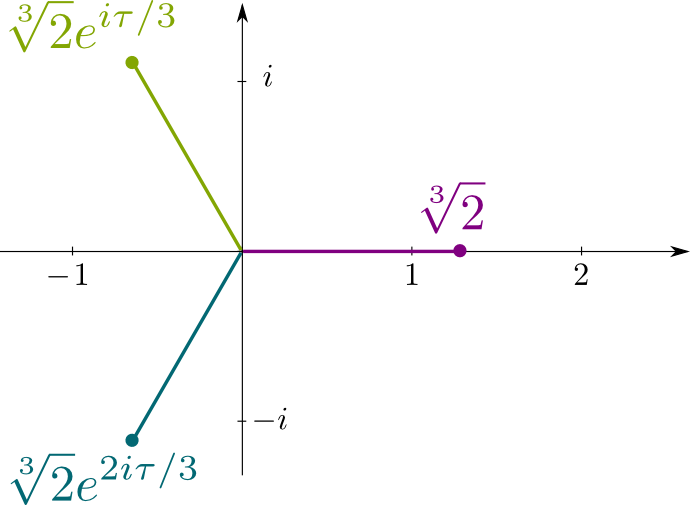
Ricordiamo che x x^3-2=0 is è l’equazione polinomiale irriducibile equation\sqrt{2} is è la soluzione di. Così, i suoi coniugati sono altre soluzioni di tale equazione, che sono i numeri complessi $\sqrt{2}j$ e $\sqrt{2}j^2$, dove $j= e^{i\tau/3}$ con $\tau = 2\pi$, essendo il rapporto tra la circonferenza di un cerchio di raggio. La figura seguente mostra le posizioni delle soluzioni coniugate in questo piano complesso:

L’ambiguità di Galois

Infine, stiamo arrivando all’intuizione chiave di Galois!

I coniugati sono perfettamente permutabili. Ciò significa che, se si modifica sistematicamente $\sqrt{2} by con il suo coniugato$- \sqrt{2}$, le uguaglianze rimangono valide. Ad esempio, dato che avevamo $1/(\sqrt{2}-1) = \sqrt{2}+1$, posso dirti semplicemente che that 1 / (- \sqrt{2}-1)=- \ sqrt{2}+1!! Allo stesso modo, abbiamo la seguente implicazione sbalorditiva:

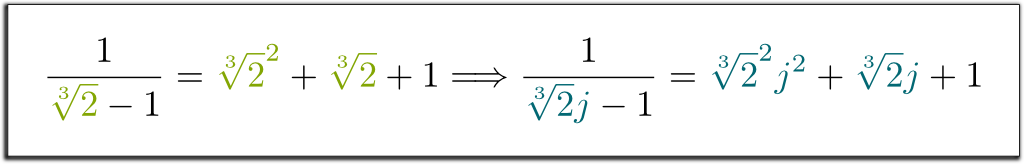
Hehe Let Vorrei prima ricordare che i campi finiti sono attraversati da un singolo elemento. Così, se il campo base è di $\mathbb Q$, qualsiasi finiti campo può essere scritto $\mathbb Q$ per alcuni destro $x_1$. Ora, consideriamo $x^n + a_{n-1}x^{n-1} $+$ … + a_1 x + a_0 = 0$ irriducibile equazione polinomiale di $x_1$ è la soluzione. Quindi, ciò che definisce $\mathbb Q$ è $\mathbb Q$-spazio vettoriale attraversato da $x_1$, $x_1^2$, …, $x_1^{n-1}$, con la semplificazione delle maggiori poteri di $x_1$, di conseguenza, la regola algebrica $x_1^n $=$ – a_{n-1}x_1^{n-1} $-$ … – a_0$.

Esattamente! Fondamentalmente, queste regole algebriche di $\mathbb Q$, in realtà non dipendono dalla natura di $x_1$; non dipende solo da un polinomio irriducibile $x_1$ è la soluzione! Pertanto, le regole di $\mathbb Q$ sono identici a questi di $\mathbb Q$, …, $\mathbb Q$, dove $x_1$, è sostituito da uno dei suoi coniugati $x_2$, …, $x_n$. In particolare, i campi math \ mathbb Q {2}] and e $\mathbb Q{2} j] operate operano in base alle stesse regole. Ecco perché i coniugati sono perfettamente permutabili! Diciamo che i campi di $\mathbb Q{2}]$ e $\mathbb Q{2} j]$ sono isomorfi, e che la sostituzione di $\sqrt{2}$ di $\sqrt{2}j$ è un isomorfismo $\mathbb Q{2}] \rightarrow \mathbb Q{2}j]$.

In un modo molto simile (ma più forte) che due spazi vettoriali della dimensione 2 sono più o meno gli stessi! Questo ha una conseguenza terribile. Significa che, da una prospettiva algebrica, non ha senso fare la differenza tra un numero e uno qualsiasi dei suoi coniugati (purché si sostituisca sistematicamente il numero con il suo coniugato)! Quindi, per esempio, algeb\sqrt{2} and e algeb-\sqrt{2} are sono algebricamente indistinguibili! Per tenerlo a mente, ecco un altro scherzo che ho inventato:

Niente affatto! Qualsiasi distinzione tra questi due numeri deve coinvolgere una matematica diversa dall’algebra, come le relazioni di ordine o la topologia. Quello che voglio dire è che, per esempio, la relazione $\sqrt{2} > 0$ fa la differenza tra $\sqrt{2}$ per $-\sqrt{2}$, ma questo perché si tratta di un ordine di relazione. Ma se ci limitiamo alle uguaglianze polinomiali, allora non c’è assolutamente alcuna differenza tra $\sqrt{2} and e$- \sqrt{2}$. Allo stesso modo, $i$ e $-i$, le soluzioni del polinomio irriducibile di equazione $x^2+1=0$, sono anche algebricamente indistinguibili. Eppure, noi chiamiamo arbitrariamente i io one uno di loro. Questo è il motivo per cui Galois chiamò la sua teoria la teoria dell’ambiguità. Oggi, l’ambiguità della scelta dei convenzionali radice quadrata di $-1$ tra $i$ e $-i$ è piuttosto chiamato la simmetria tra $i$ e $-i$.

Gruppi di Galois

Galois si è particolarmente concentrato sulle estensioni di campo che sono stabili per coniugazione. Tali estensioni di campo stabili sono ora conosciute come estensioni Galois. Quindi, se $x_1$ appartiene a una estensione di Galois, quindi questa estensione di Galois contiene tutti i suoi coniugati $x_2$, …, $x_n$.

Un modo semplice per costruire estensioni di Galois consiste nel prendere il campo attraversato da soluzioni di un’equazione polinomiale irriducibile. Per esempio, se $x_1$, …, $x_n$ sono coniugati per il campo base di $\mathbb Q$, allora $\mathbb Q / \mathbb Q$ è un estensione di Galois. I campi costruiti in questo modo sono chiamati campi di divisione.

Ad esempio, il campo di divisione dell’equazione x x^3-2=0 is è l’estensione di Galois \\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \ mathbb Q sp attraversato dalle sue soluzioni.

Se x x_1 sp si estende su un’estensione di Galois, allora anche i suoi coniugati. Quindi, \ \ mathbb Q = \ mathbb Q = $ … $ =\mathbb Q = = \ \ mathbb Q$. Così, l’isomorfismo tra $\mathbb Q$ e $\mathbb Q$ che consiste nell’sempre sostituendo $x_1$ da $x_2$ è infatti un isomorfismo tra $\mathbb Q$ e a se stesso! Lo chiamiamo automorfismo. Automorfismi di un’estensione di Galois forms\mathbb Q/ \ mathbb Q forms forma il gruppo di Galois Gal Gal (\mathbb Q/ \ mathbb Q)$.

Ora, il che è fondamentale, se $\mathbb Q = \mathbb Q$, quindi tutti automorsmi di una estensione di Galois $\mathbb Q/ \mathbb Q$ sono le permutazioni di $x_1$, con uno dei suoi coniugati! In particolare, vediamo qui che la cardinalità di un gruppo di Galois è uguale al grado dell’estensione di Galois.

Certo! Si può notare che $\mathbb Q = \mathbb Q$ e $\mathbb Q = \mathbb Q$, il che significa che $i$ e $\sqrt{2}$ ogni campate suddivisione dei campi di irriducibile equazione polinomiale sono soluzione. Quindi, extensions\mathbb Q/\mathbb Q and e both\mathbb Q/ \ mathbb Q are sono entrambe estensioni di Galois. Pertanto, la loro automorsmi consistono nella sostituzione $i$ da uno dei suoi coniugati, $i$ o $-i$, e la sostituzione di $\sqrt{2}$ di $\sqrt{2}$ o per $-\sqrt{2}$. Nei primi casi, non stiamo cambiando nulla in numeri, che corrisponde alla simmetria zero. I secondi casi possono essere visualizzati come simmetrie assiali, come mostrato nella figura seguente:

Non è sorprendente?

Certo! Arriviamo al campo di divisione \ \ mathbb Q {2}, \ sqrt{2} j, \sqrt{2} j^2] of di x x ^ 3-2=0.. Ma, prima di andare oltre, notiamo che \\mathbb Q{2}, \ sqrt{2}j, \sqrt{2} j^2] = \ mathbb Q {2}, j]$.

Tutto quello che dobbiamo dimostrare è che tutti i generatori di un campo appartengono all’altro. Iniziamo dimostrando che i generatori di quest’ultimo, $\sqrt{2}$ e j j belong, appartengono al primo. È ovvio per $ \ sqrt{2}$. Ora, $j = (\sqrt{2} j) / \sqrt{2}$, quindi belong j belong appartiene anche al campo precedente. Ciò dimostra che tutti gli elementi di Q \ mathbb Q {2}, j] belong appartengono a to\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2]$. Reciprocamente, è semplice che tutti i generatori dell’ex campo $\sqrt{2}$, $\sqrt{2}j$ e $\sqrt{2}j^2$, sono prodotti di generatori di quest’ultimo. Pertanto, entrambi i campi sono uguali. E, in particolare, $ \ mathbb Q {2}, j] / \ mathbb Q is è un’estensione di Galois.

Hehe He Per capire le simmetrie di math\mathbb Q{2}]$, dovremo andare oltre nello studio di Galois dei gruppi di Galois

Corrispondenza di Galois

Il problema con i gruppi di Galois è che possono diventare estremamente grandi e complicati. Questo è particolarmente il caso del gruppo infinito Gal Gal (\bar {\mathbb Q}/ \ mathbb Q)$. Per catturare gruppi così grandi e complessi, Galois ebbe la brillante idea di spezzarli in pezzi più piccoli.

Sorprendentemente, Galois ha scoperto che i gruppi di Galois potrebbero essere suddivisi in sottogruppi di simmetrie solo guardando quelli che lasciano invariati alcuni sottocampi. Ad esempio, $\mathbb Q is è un sottocampo di$ \mathbb Q{2}, j]$, poiché qualsiasi numero del primo appartiene al secondo. Così, simmetrie di $\mathbb Q{2},j]$ che non cambia nulla a $\mathbb Q$ formare un sottogruppo del gruppo di Galois di $\mathbb Q{2},j]/\mathbb Q$. Queste simmetrie formano il gruppo di Galois Gal Gal (\mathbb Q{2},j]/ \ mathbb Q)$.

Lo so! Mi piace visualizzare queste simmetrie come i modi per collegare onto \ mathbb Q{2},j] onto su onto \ mathbb Q$. Ecco un’immagine immaginata del “collegare”:

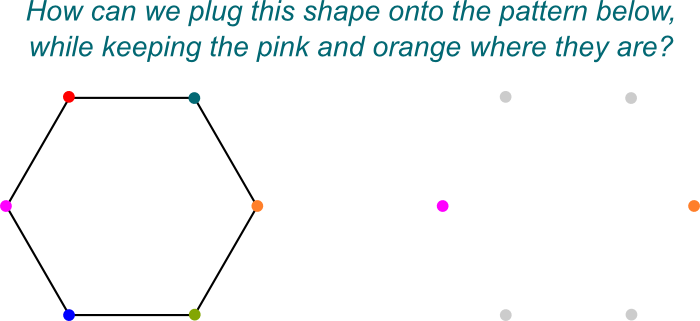
Esattamente! E questo semplicemente perché $\mathbb Q{2},j]$ è un estensione di Galois di $\mathbb Q$ che è di per sé un campo di estensione di $\mathbb Q$.

E c’è di più! Galois ha mostrato che tutti i sottogruppi di estensioni di Galois sono ottenuti in questo modo! Più precisamente, la mappatura di un qualsiasi campo $K$ in-tra l’estensione di Galois $\mathbb Q{2},j]$ e il campo base di $\mathbb Q$ per il gruppo di Galois $Gal(\mathbb Q{2},j] / K)$ è biunivoca. Questo fatto è chiamato la corrispondenza di Galois! Questa corrispondenza è schematicamente visualizzata di seguito per un’estensione Galois \ \ mathbb Q / \ mathbb Q$.

Invece di cercare di descrivere direttamente questo gruppo, concentriamoci sul suo sottogruppo Gal Gal(\mathbb Q{2}, j] / \mathbb Q)$. È semplice che $\sqrt{2}$ si estende su $\mathbb Q{2},j]$ quando aggiunto a $\mathbb Q$. Quindi, $ \ mathbb Q {2}, j]/ \ mathbb Q is è un’estensione di Galois estesa da $\sqrt{2}$. Pertanto, l’utilizzo di un teorema che abbiamo visto in precedenza, sappiamo che tutti automorsmi di questa estensione di Galois consistono nella sostituzione di $\sqrt{2}$ da parte di uno dei suoi 3 coniugati (di per sé, $\sqrt{2} j$ e $\sqrt{2} j^2$)!

Ora, potrei continuare a studiare altri pezzi di Gal Gal(\mathbb Q{2}, j]/\mathbb Q) like, come il sottogruppo di Galois Gal Gal(\mathbb Q{2},j] / \mathbb Q{2}])$. Ma preferisco usare un altro dei potenti teoremi di Galois. Vale a dire, ha dimostrato che se $\mathbb Q/\mathbb Q was era inoltre un’estensione di Galois stessa, allora il sottogruppo Gal Gal(\mathbb Q{2}, j]/\mathbb Q) is è normale.

Quindi, il gruppo di Galois di this\mathbb Q{2},j]/\mathbb Q can può essere quozientato da questo sottogruppo, e il gruppo del quoziente è quindi uguale a Gal Gal(\mathbb Q / \mathbb Q)$. Eppure, $\mathbb Q/\mathbb Q$ è infatti un’estensione di Galois attraversato da $j$, la cui coniugato è di $j^2$. Così, $Gal(\mathbb Q/\mathbb Q)$ è costituito in entrambi lasciando $j$ come $j$ o la sua sostituzione con $j^2$.

ora Siamo in grado di dedurre tutte le simmetrie di $Gal(\mathbb Q{2},j]/\mathbb Q)$ combinando questi di $Gal(\mathbb Q{2},j] / \mathbb Q)$ e $G(\mathbb Q/\mathbb Q)$. Siamo in grado di visualizzare queste simmetrie dal disegno di come influenzano le nostre tre spanning coniugati $\sqrt{2}$, $\sqrt{2}j$ e $\sqrt{2}j^2$:

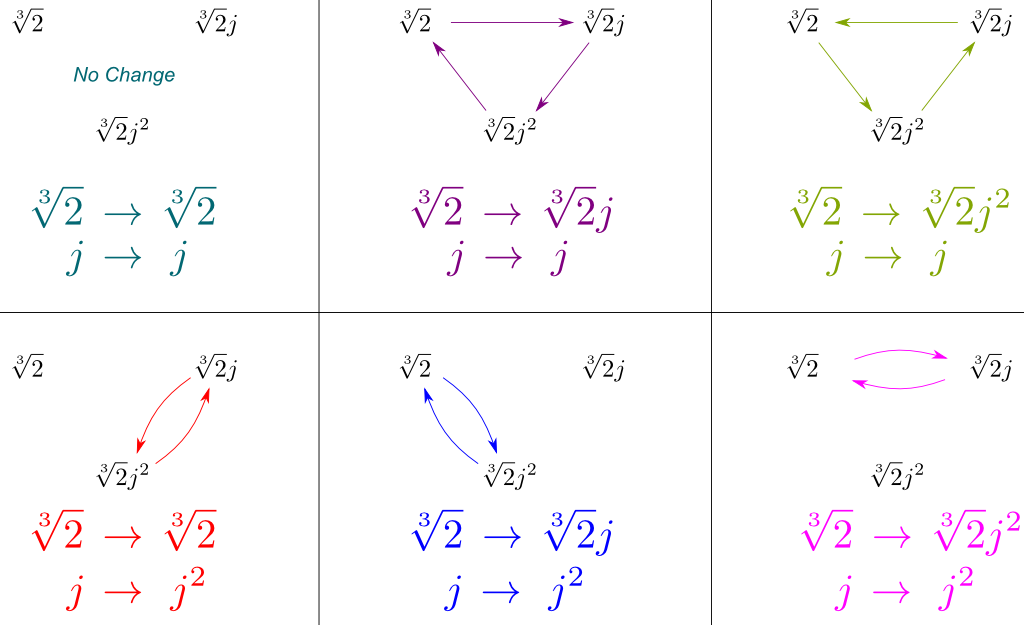
Fondamentalmente, la figura sopra contiene tutte le simmetrie di Gal Gal(\mathbb Q{2},j] / \mathbb Q)$. E sorprendentemente, queste simmetrie corrispondono al noto gruppo di simmetria.

Lascerò che Marcus du Sautoy te lo presenti:

Quindi, le simmetrie qui sono come una stella marina o come un triangolo?

Sì, davvero! Questo gruppo di simmetrie del triangolo è chiamato D D_3_, ed è lo stesso del gruppo perm S_3 of di permutazioni di 3 elementi. Questo ci porta alla seguente formula, che ho trovato così bella, che ho deciso di inquadrarla!

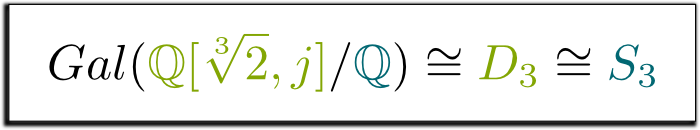
Concludiamo

In molti modi, Galois deve essere considerato il padre dell’algebra moderna. La sua intuizione chiave è stata quella di guardare la matematica attraverso l’angolo delle regole delle operazioni, e questo lo ha portato a svelare ambiguità sorprendenti e penetranti, o simmetrie, tra i numeri. Da una prospettiva algebrica, numeri, come $\sqrt{2}$, $\sqrt{2}j$ e $\sqrt{2}j^2$ sono, infatti, perfettamente simmetrica e totalmente intercambiabili.

La comprensione di queste simmetrie ha avuto applicazioni sorprendenti in geometria algebrica e topologia algebrica, tra gli altri. In particolare, i primi successi della teoria includono una classificazione dei poligoni regolari costruibili e un teorema che afferma che le equazioni polinomiali ad alto grado non possono essere risolte dai radicali.