Prealgebra
Risultati di Apprendimento
- Trovare l’area di base e l’altezza di un triangolo
- Trovare la lunghezza di un lato di un triangolo dato il perimetro e di altre due lunghezze
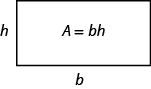
ora sappiamo come trovare l’area di un rettangolo. Possiamo usare questo fatto per aiutarci a visualizzare la formula per l’area di un triangolo. Nel rettangolo sottostante, abbiamo etichettato la lunghezza b e la larghezza h, quindi la sua area è bh.
L’area di un rettangolo è la base, b, volte l’altezza, h.
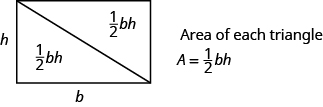
Possiamo dividere questo rettangolo in due triangoli congruenti (vedi l’immagine sotto). I triangoli congruenti hanno lunghezze e angoli laterali identici, e quindi le loro aree sono uguali. L’area di ogni triangolo è la metà dell’area del rettangolo, o \frac{1}{2}bh. Questo esempio ci aiuta a capire perché la formula per l’area di un triangolo è A=\frac{1}{2}bh.
Un rettangolo può essere diviso in due triangoli di area uguale. L’area di ciascun triangolo è metà dell’area del rettangolo.
La formula per l’area di un triangolo è A=\frac{1}{2}bh, dove b è la base e h è l’altezza.
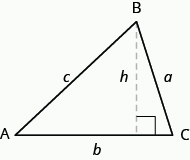
Per trovare l’area del triangolo, è necessario conoscere la sua base e l’altezza. La base è la lunghezza di un lato del triangolo, di solito il lato in basso. L’altezza è la lunghezza della linea che collega la base al vertice opposto e crea un angolo \text{90}^ \ circ con la base. L’immagine qui sotto mostra tre triangoli con la base e l’altezza di ciascuno contrassegnati.
L’altezza h di un triangolo è la lunghezza di un segmento di linea che collega la base al vertice opposto e crea un angolo \text{90}^ \circ con la base.

Proprietà del triangolo
Per qualsiasi triangolo \Delta ABC, la somma delle misure degli angoli è \text{180}^ \circ.
m\angle{A}+m\angle{B}+m\angle{C}=180^\circ
Il perimetro di un triangolo è la somma delle lunghezze dei lati.
P=a+b+c
L’area di un triangolo è la metà della base, b, volte l’altezza, h.
A=\frac{1}{2}bh
esempio
Trova l’area di un triangolo la cui base è di 11 pollici e la cui altezza è di 8 pollici.
Soluzione
| Passaggio 1. Leggi il problema. Disegna la figura e etichettala con le informazioni fornite. | 
|
| Passaggio 2. Identificare ciò che si sta cercando. | l’area del triangolo |
| Passo 3. Nome. Scegli una variabile per rappresentarla. | lasciare A = area del triangolo |
| Passo 4.Tradurre.
Scrivi la formula appropriata. Sostituto. |
 |
| Passaggio 5. Risolvi l’equazione. | A = 44 pollici quadrati. |
| Passaggio 6. Controllo:
A= \ frac{1}{2}bh 44\stackrel{?} {=} \frac{1}{2}(11)8 44=44\segno di spunta |
|
| Passaggio 7. Rispondi alla domanda. | L’area è di 44 pollici quadrati. |
provalo
esempio
Il perimetro di un giardino triangolare è di 24 piedi. Le lunghezze di due lati sono 4 piedi e 9 piedi. Quanto è lungo il terzo lato?
provalo
esempio
L’area di una finestra triangolare della chiesa è di 90 metri quadrati. La base della finestra è di 15 metri. Qual è l’altezza della finestra?
provalo
Triangoli isosceli e equilateri
Oltre al triangolo rettangolo, alcuni altri triangoli hanno nomi speciali. Un triangolo con due lati di uguale lunghezza è chiamato triangolo isoscele. Un triangolo che ha tre lati di uguale lunghezza è chiamato triangolo equilatero. L’immagine qui sotto mostra entrambi i tipi di triangoli.
In un triangolo isoscele, due lati hanno la stessa lunghezza e il terzo lato è la base. In un triangolo equilatero, tutti e tre i lati hanno la stessa lunghezza.
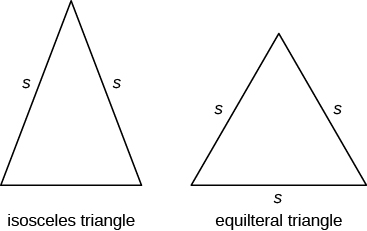
Triangoli isosceli e equilateri
Un triangolo isoscele ha due lati della stessa lunghezza.
Un triangolo equilatero ha tre lati di uguale lunghezza.
esempio
Il perimetro di un triangolo equilatero è di 93 pollici. Trova la lunghezza di ciascun lato.
try it
example
Arianna has 156 inches of beading to use as trim around a scarf. La sciarpa sarà un triangolo isoscele con una base di
60 pollici. Quanto tempo può fare i due lati uguali?








