Una parte integrante della fluidodinamica è la vorticità. Euristicamente, misura la rotazione locale di un pacco fluido. Per gli oggetti solidi non parliamo della vorticità di un oggetto, ma invece ci riferiamo alla sua velocità angolare. Questi due concetti sono correlati, ma la vorticità è più utile quando si parla di oggetti rotanti che si deformano, come fa un fluido.

La vorticità di un dato campo di velocità all’interno di un dato piano, viene calcolata scegliendo due assi ortogonali in quel piano e aggiungendo la velocità angolare di ciascun asse. In un oggetto solido, o un fluido che ruota come un oggetto solido (giustamente chiamato rotazione del corpo solido), la vorticità è il doppio della velocità angolare poiché ogni asse ruota alla stessa velocità. Tuttavia in un fluido i due assi possono ruotare a velocità molto diverse e anche in direzioni diverse! È anche possibile che ogni asse possa ruotare ma la vorticità netta è zero (vedi vortice irrotazionale).

Se il movimento di un fluido è strettamente limitato a trovarsi in un piano, il vettore di vorticità è considerato ortogonale al piano e non può cambiare direzione (o inclinazione). L’unico aspetto della vorticità che può cambiare è la sua grandezza. Si ritiene che questo trasferimento di energia a scale più grandi sia collegato alla formazione della Grande Macchia Rossa su Giove.

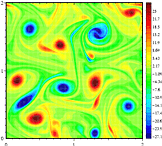
Nel movimento tridimensionale del fluido il vettore vorticità è tridimensionale in quanto ha componenti paralleli a ciascun asse, x, y e z: il componente z è parallelo all’asse z e descrive la velocità di rotazione nel piano xy. È a causa di questa dicotomia che esiste una differenza qualitativa nel comportamento tra turbolenza bidimensionale e turbolenza tridimensionale. Nel primo c’è una tendenza per i vortici a raggrupparsi e formare vortici più grandi, mentre nel secondo i moti vortici sono lacerati e l’energia scende a cascata fino alle scale più piccole dove viene poi diffusa via.

Matematicamente, la vorticità di un determinato campo di velocità,

è definito come il ricciolo del campo di velocità, e di solito è indicato con la lettera greca omega,

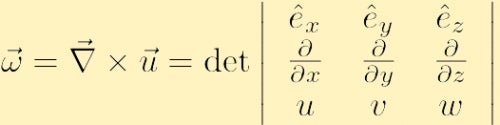
dove abbiamo usato il convenzionale nabla simbolo per il gradiente:

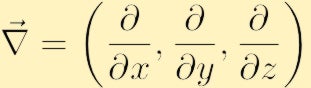
Nella forma componente la vorticità si trova espandendo il determinante sopra,

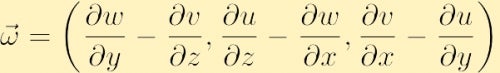
Un altro aspetto importante della fluidodinamica che è correlato alla vorticità è la circolazione. A differenza della vorticità che è una proprietà locale, definita in ogni punto dello spazio, la circolazione è una proprietà globale, definita integrando una proprietà del fluido su una curva. In particolare, se prendi una qualsiasi contorno chiuso e indica con la lettera C(t) la circolazione intorno a C(t), in senso antiorario, è una quantità scalare indicate,

è definito come:

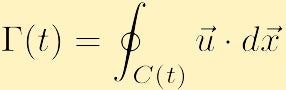
che può essere una funzione del tempo, così come il contorno chiuso.

Prendiamoci un momento per spiegare cosa sta dicendo fisicamente. In ogni punto del contourC (t) troviamo la componente della velocità tangente alla curva e moltiplichiamo questo scalare per una lunghezza infinitesimale; proiettare la velocità sulla tangente darà necessariamente una grandezza tra la velocità in quella posizione e zero. Se la velocità è tangente alla curva, otteniamo più o meno la velocità di, se la velocità è ortogonale alla curva, otteniamo zero. Quindi integriamo questa quantità, un modo diverso di dire sommando un numero infinito di cose, attorno al contorno in modo da aggiungere il contributo da ogni punto. Da ciò si accerta che la circolazione lungo un contorno C (t) è la quantità di flusso attorno al contorno (t); un risultato positivo o negativo corrisponde al contorno in senso orario o alla circolazione in senso orario, rispettivamente. Un caso estremo è dove il campo di velocità è ovunque perpendicolare alla curva C (t) e di conseguenza non c’è circolazione poiché il flusso attraversa sempre il contorno e non scorre mai lungo il contorno. Per ottenere una circolazione diversa da zero ci deve essere una parte della curva in cui il flusso è lungo il contorno chiuso.

Se il campo di velocità è liscio e non ci sono singolarità all’interno di C(t) possiamo quindi utilizzare Stokes’ Integrale Teorema per il calcolo vettoriale di riscrivere la circolazione,

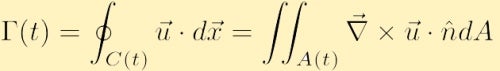
dove A è l’area contenuta all’interno del contorno C e ä è l’unità di vettore normale al areaA.

Prima di contemplare questa nuova equazione per la circolazione è utile comprendere il significato fisico per il Teorema di Stokes dove il campo vettoriale è la velocità. Nel doppio integrale sopra calcoliamo la vorticità in ogni punto all’interno del contorno e quindi riassumiamo la vorticità su tutti questi punti in A(t). Nel singolo integrale sopra il contorno chiuso stiamo calcolando il flusso lungo il confine dell’area. Il teorema di Stokes afferma quindi che queste quantità sono uguali, e quindi che se c’è vorticità media all’interno di un’area, che deve quindi significare che l’area ha una velocità di rotazione diversa da zero, ci deve di conseguenza essere una circolazione netta lungo il perimetro di quel confine.

Dal Teorema del valore medio del calcolo possiamo sostituire l’integrando nel doppio integrale con un valore medio, che corrisponde alla componente media della vorticità ortogonale al piano in cui si trova C(t). Quindi, la seconda interpretazione della circolazione è che è la vorticità media per l’area contenuta in C (t). Invece di calcolare la circolazione sul contorno chiuso C (t) possiamo calcolare la vorticità media normale ad A(t) e moltiplicarla per l’area all’interno. Se si considera il caso speciale in cui la vorticità è ovunque costante, la circolazione sarebbe la grandezza della vorticità volte l’area contenuta all’interno.

Un vortice puntiforme è un vortice che non ha area, il che significa che la vorticità è presente solo in un singolo punto. Per studiare i vortici puntuali assumeremo innanzitutto che abbiamo un flusso incomprimibile 2D. (I vortici puntuali sono talvolta indicati anche come vortici di linea se visualizzati in 3D.)

Dopo alcuni calcoli si ritiene che il campo di velocità che viene generato da un punto di vortice, in forma complessa, che si trova a z0 è dato da (dove Gamma zero è la circolazione intorno al punto di vortice, che è spesso definito come la forza del punto di vortex):

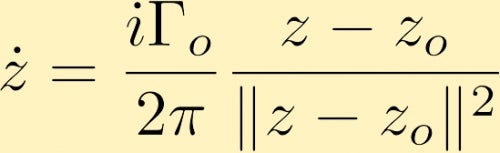
Il campo di velocità generati da un punto di vortice può causare un altro punto di vortice a muoversi. Ecco alcuni esempi di questo: I due vortici puntiformi, entrambi positivi e di uguale grandezza, i due vortici puntiformi, entrambi positivi ma uno ha il triplo della forza dell’altro e un vortice puntiforme è negativo con il doppio della grandezza dell’altro che è positivo . Un’altra possibilità è quella di considerare due vortici puntiformi della stessa grandezza ma di segno opposto.

Questo può essere esteso a qualsiasi numero di vortici di punti, N. L’equazione del moto in forma complessa per un vortice di punti alfa è data da:

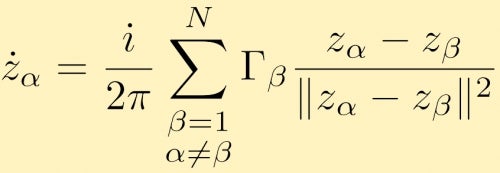
Guardare le interazioni dei vortici puntiformi è un problema molto interessante che è difficile da fare analiticamente, specialmente quando aumenta il numero di vortici puntiformi. Simulazioni numeriche di interazioni punto vortice è quindi molto comune. Un’applicazione utile delle simulazioni di vortici di grandi punti è se si osservano grandi gruppi di vortici puntiformi che simulano vortici con area finita. Ecco le descrizioni e i risultati di diverse simulazioni di vortici a punti grandi. In questo caso abbiamo due grandi gruppi di vortici puntiformi di uguale forza che si fondono. Nel caso successivo iniziamo con un anello di veracità di punti raggruppati.

Per trovare un’equazione per l’evoluzione della vorticità iniziamo con l’equazione della quantità di moto. Nell’equazione della quantità di moto il termine advective può essere riscritto come segue,

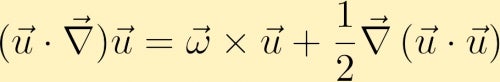
Successivamente calcoliamo il ricciolo dell’equazione della quantità di moto e attraverso alcune identità vettoriali otteniamo l’equazione della vorticità:

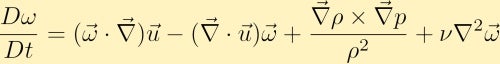
L’equazione della vorticità mostra come la vorticità può essere generata in un fluido. Senza perdita di generalità assumeremo che inizialmente abbiamo solo vorticità nella direzione z. Da questo possiamo vedere come ciascuno dei quattro termini diversi può alterare la vorticità.

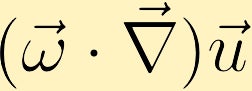
Se c’è un cambiamento nella velocità con la direzione della vorticità esistente, la vorticità può essere generata.

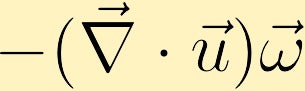
Se un pacco fluido si sta espandendo e la vorticità è positiva, la vorticità del pacco fluido diminuirà e se il pacco si sta contraendo la vorticità aumenterà.

Gli strati fluidi a densità costante (isopicnali) vogliono coincidere con gli strati a pressione costante (isobari). Se questi strati non coincidono, il fluido inizia a ruotare per renderli allineati, il che causa la vorticità. (Nell’esempio iniziamo con vorticità zero.)

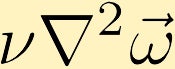
Le forze viscose causano la diffusione della vorticità. (Nell’esempio iniziamo con un punto di vorticità infinita al centro.)