トロイダルインダクタと変圧器
いくつかの状況では、トロイダルインダクタの巻線の電流は巻線内のB磁場にのみ寄与し、巻線外の磁気B磁場には寄与しない。 これは対称性とアンペールの円環則の結果である。
Bフィールドエディットの総内部閉じ込めのための十分な条件
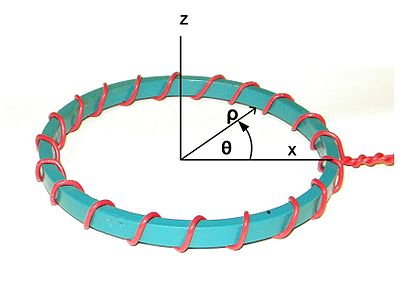  1. 座標系。 Z軸は、公称対称軸である。 X軸は、巻線の開始点と整列するように任意に選択されます。 θは半径方向と呼ばれます。 θは円周方向と呼ばれます。
|
 図。 2. 円周電流のない軸対称トロイダルインダクタ。
|
円周電流の欠如(円周電流の経路は、このセクションの図3の赤い矢印で示されています)と導体と磁性材料の軸対称 (一部の著者は、Hフィールドを使用することを好む)。 対称性のために、Bフラックスの線は、対称軸を中心とする一定の強度の円を形成しなければならない。 電流を取り囲むB磁束の唯一の線は、トロイダル巻線の内側にある線です。 したがって、アンペアのcircuital法則から、B磁場の強度は巻線の外側でゼロでなければなりません。

このセクションの図3は、最も一般的なトロイダル巻線を示しています。 これは、合計Bフィールドの閉じ込めの両方の要件に失敗します。 軸から外を見ると、時には巻線がコアの内側にあり、時にはコアの外側にあることがあります。 近傍領域では軸対称ではありません。 しかし、巻線間隔の数倍の距離の点では、トロイドは対称的に見えます。 まだ円周電流の問題があります。 巻線がコアを取り囲んでいても、ワイヤがどんなに薄くても、このトロイダルインダクタは、トロイドの平面に1つのコイルループを含みます。 この巻線はまた、インダクタの平面内でE磁場を生成し、その影響を受けやすくなります。
図4-6は、円周方向の電流を中和するさまざまな方法を示しています。 図4は最も単純なもので、インダクタを購入または構築した後に戻り線を追加できるという利点があります。
  図。 4. 帰りのワイヤーと対抗される円周の流れ。 ワイヤーは白く、誘導器の外の縁と巻上げの外の部分の間で動く。
|
 図。 5. 周方向の電流は戻り巻線で対抗した。
|
 図。 6. 周方向電流はスプリットリターンワインディングで対抗しました。
|
E field in the plane of the toroidEdit
 Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.
|
 Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.
|
巻線に沿って電位の分布があります。 これにより、図7に示すように、トロイドの平面内にEフィールドが発生し、トロイドの平面内にEフィールドに対する感受性が発生する可能性があります。 これは、図8に示すように戻り巻線を使用することによって軽減することができます。 この巻線では、巻線が交差するそれぞれの場所で、2つの部分は等しく反対の極性になり、平面内で生成されるE磁場が実質的に減少します。
トロイダルインダクタ/トランスと磁気ベクトル電位編集

磁気ベクトルポテンシャルの一般的な議論については、ファインマン第14章と第15章を参照してください。 長く薄いソレノイドの周りの磁気ベクトルポテンシャルの図については、ファインマン15-11ページを参照してください。
a体は、b f A=0{\displaystyle bf{A}=0}

という仮定を用いるときに正確である。 これは、
- 1という仮定の下で真となります。 クーロンゲージは
- 2を使用します。 ローレンツゲージが使用されており、電荷の分布は存在せず、ρ=0{\displaystyle\rho=0\,}
- 3。 ローレンツゲージが使用され、ゼロ周波数は
- 4と仮定されます。 ローレンツゲージが使用され、1c2≤t{\displaystyle{\frac{1}{c^{2}}}{\frac{\partial\phi}{\partial t}}}
を無視するのに十分低い非ゼロ周波数が仮定される。
番号4は、このセクションの残りの部分について推定され、”準静的条件”と呼ばれることがあります。
円周電流のない軸対称トロイダルインダクタは巻線内にB磁場を完全に閉じ込めますが、A磁場(磁気ベクトル電位)は閉じ込められません。 写真の矢印#1は、対称軸上のベクトルポテンシャルを示しています。 半径方向の電流セクションaとbは、軸から等しい距離ですが、反対方向に向けられているため、キャンセルされます。 同様に、セグメントcとdはキャンセルします。 実際には、すべての半径方向の電流セグメントがキャンセルされます。 軸方向電流の状況は異なります。 トロイドの外側の軸方向の電流が下に向けられ、トロイドの内側の軸方向の電流が上に向けられています。 トロイドの外側の各軸方向電流セグメントは、トロイドの内側の等しいが反対方向のセグメントと一致させることができる。 内側のセグメントは、外側のセグメントよりも軸に近いため、対称軸に沿ってaフィールドの正味の上向き成分があります。

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂E∂t→0{\displaystyle{\frac{\partial E}{\partial t}}\rightarrow0}

)は同じ形をしているので、Aの線と等高線はbの線と等高線と同様にbに関係している。電流のループの周りのbフィールドと同じです。 左の図は、トロイダルインダクタの周りのaフィールドのアーティストの描写です。 太い線は、より高い平均強度のパスを示します(短いパスは、パス積分が同じになるように、より高い強度を持っています)。 ラインはちょうどよく見て、フィールドの一般的な外観を与えるために描かれています。
全b場閉込めの存在下でのトロイダル変圧器の作用編集
E場とB場は、aとπ{\displaystyle\phi\,}

(スカラー電位)場B=Π×Aから計算することができる。 {\displaystyle\mathbf{B}=\nabla\times\mathbf{A}。

と:E=−∞−∞a∈t{\displaystyle\mathbf{e}=-\nabla\phi-{\frac{\partial\mathbf{a}}{\partial t}}}

だから、外側の領域が巻線はbフィールドを欠いており、非ゼロのEフィールドで満たされています。 量σ a∈t{\displaystyle{\frac{\partial\mathbf{A}}{\partial t}}}

は一次と二次の間の望ましい磁場結合を担当し、量σ{\displaystyle\nabla\phi\,}

は、一次と二次の間の望ましくない電界結合を担当しています。 変圧器の設計者は、電界結合を最小化しようとします。 このセクションの残りの部分については、特に指定がない限り、∇ ϕ{\displaystyle\nabla\phi\,}

はゼロであると仮定される。
ストークスの定理が適用されるので、パス積分Bが囲まれた電流の一定の倍に等しいのと同じように、aのパス積分が囲まれたB磁束に等しいように
二次巻線に沿ったEのパス積分は、二次の誘導起電力(電気原動力)を与える。
E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

これは、EMFがBの時間変化率に等しいと通常の結果である巻線によって囲まれた磁束。
トロイダルトランスポインティングベクトルは、総Bフィールド閉じ込めeditの存在下で一次から二次への結合


figureEditの説明
この図は、トロイダル変圧器の半分のセクションを示しています。 準静的条件が仮定されるので、各フィールドの位相はどこでも同じです。 変圧器、その巻線、およびすべてのものは、対称軸の周りに対称的に分布しています。 巻線は、円周方向の電流がないようなものである。 第一次流れによるB分野の完全な内部閉じ込めのための条件は満たされる。 コアと一次巻線は灰褐色のトーラスで表されます。 一次巻線は示されていませんが、断面面での巻線の電流は金(またはオレンジ)の楕円として示されています。 一次電流によって引き起こされるB電界は、一次巻線(すなわちコア)によって囲まれた領域に完全に限定される。 左側の断面の青い点は、コア内のBフラックスの線が左側の断面から出てくることを示しています。 他の断面では、青色のプラス記号は、Bフラックスがそこに入ることを示しています。 一次電流から供給されるEフィールドは、緑色の楕円として示されています。 二次巻線は、対称軸の下に直接来る茶色の線として示されています。 通常の練習では、二次の両端はトーラスから十分に離れた長いワイヤと一緒に接続されていますが、絶対的な軸対称性を維持するために、装置全体が完全に導電性の球の内側にあると想定され、二次ワイヤは各端部で球の内側に”接地”されています。 二次は抵抗ワイヤーから成っています、従って別の負荷がありません。 二次に沿ったEフィールドは、二次(黄色の矢印)に電流を引き起こし、二次の周りにBフィールドを引き起こします(青い楕円として示されています)。 このBフィールドは、変圧器コアの内部を含む空間を埋めるので、二次側が開いていない場合、最終的には、一次側から二次側への連続的な非ゼロBフィールド E場(一次電流から供給される)とB場(二次電流から供給される)の交差積は、一次から二次に向かって指すポインティングベクトルを形成する。

