水素原子シュレーディンガー方程式の解は、球面調和関数と動径関数の積である関数です。水素原子の波動関数は、3つの変数r、\(\theta\)、および\(\varphi\)と3つの量子数n、\(l\)、および\(m_l\)に依存します。 これらの変数は、陽子に対する電子の位置を球面座標で与えます。 波動関数の絶対二乗|psi(r,\theta,\varphi)|2 2\)は、\(r\)、\(\theta\)、\(\varphi\)で評価され、r、\(\theta\)、\(\varphi\)で指定された位置を中心とする微分体積\(d\tau\)内の電子を見つける確率密度を与えます。p>

整数の値は何ですか

\

量子数には名前があります: \(n\)は主量子数と呼ばれ、\(l\)は角運動量量子数と呼ばれ、\(m_l\)は磁場中のエネルギーが\(m_l\)に依存するため、磁気量子数と呼ばれます。\(m_l\)は\(m_l\)に依存します。\(m_l\)は\(m_l\)に依存します。\(m_l\)は\(m_l\)に依存します。\(m_l\)は\(m_l\) \(L\)は、方位角\(\Theta\)を含む\(\theta\)方程式の結果であるため、しばしば方位角量子数と呼ばれ、天頂への角度を参照します。\(\theta\)は、\(\theta\)の逆数です。\(\theta\)は、\(\theta\)の逆数です。\(\theta\)は、\(\theta\)の逆数です。\(\theta\

これらの量子数は、シュレーディンガー方程式に課される物理的制約または境界条件によって決定される特定の値を持っています。

: \(n\)は0より大きい整数でなければならず、\(l\)は0からn‑1までの値を持つことができ、\(m_l\)は\(-l\)から\(+l\)までの範囲の値を単位または整数ステッ 量子数\(l\)の値は通常、文字で符号化されます：sは0を意味し、pは1を意味し、dは2を意味し、fは3を意味し、次の符号はアルファベット順に続きます（例えば、gは\(l=4\)を意味します）。 量子数は物理量の量子化を指定します。 水素原子の異なる状態の離散エネルギーは\(n\)で与えられ、角運動量の大きさは\(l\)で与えられ、角運動量の1つの成分（通常は化学者によってz成分 特定の値が\(n\)の軌道の総数は\(n^2\)です。P>

運動\(\PageIndex{2}\)

nのいくつかの値を考え、各nの軌道の数が\(n^2\)であることを示します。Exercise\(\PageIndex{3}\)\(\PageIndex{3}\)\(\PageIndex{3}\)\(\pageindex{3}\)\(\pageindex{3}\)\(\PageIndex{3}\)\(\PageIndex{3}\)\(\PageIndex{3}\)\(\PageIndex{3}\)\(\PageIndex{3 水素のエネルギーレベル1から7のため。3dという表記は、水素原子内の電子の量子数を指定します。 Nと\(l\)の値は何ですか？ エネルギーと角運動量の値は何ですか？ 磁気量子数の可能な値は何ですか？ 角運動量ベクトルの可能な向きは何ですか？水素原子波動関数\(\psi(r,\theta,\varphi)\)は原子軌道と呼ばれます。 原子軌道は、原子内の1つの電子を記述する関数です。 N=1、\(l=1\)、\(m_l\)=0の波動関数は1s軌道と呼ばれ、この関数によって記述される電子はls軌道にある、すなわち1s軌道状態を持つと言われます。 水素原子シュレーディンガー方程式の解の間に課される\(n\)、\(l)\)、および\(m_l\)の制約は、なぜ単一の1s軌道があるのか、なぜ3つの2p軌道、5つの3d軌道などがあるのかを説明する。 私たちは、これらの制約が周期表の特徴を説明することを第9章で多電子原子を考慮するときに表示されます。 言い換えれば、周期表はシュレーディンガー模型と水素原子に対するシュレーディンガー方程式の解を得るために課される物理的制約の現れである。\(\theta\)と\(\varphi\)を使って電子波動関数の変化を可視化することは、波動関数の絶対二乗が原子または分子内の電荷分布（電子確率密度）を表すので重要です。\(\theta\)と\(\varphi\)を使って電子波動関数の変化を可視化することは重要です。 電荷分布は化学反応性に関連しているため、化学の中心です。 例えば、ある分子の電子欠損部分は別の分子の電子に富む領域に引き寄せられ、そのような相互作用は置換および付加反応からタンパク質の折り畳みおよび基質と酵素との相互作用に至るまでの化学的相互作用において主要な役割を果たす。

波動関数と電荷分布を視覚化することは、三次元空間における三つの変数の関数の挙動を調べる必要があるため、困難です。 この可視化は、半径と角度の部分を別々に考慮することによって容易になりますが、半径と角度の部分を別々にプロットしても、軌道の形状はあまりよく 形状は、確率密度プロットでよりよく明らかにすることができます。 このような3次元プロットを作成するには、スペースを小さなボリューム要素に分割し、各ボリューム要素の中心で\(\psi^*\psi\)を計算し、そのボリューム要素を\(\psi^*\psi\)の大きさに比例して陰影、点描、色付けします。 このようなプロットを類似した極座標プロットと混同しないでください。確率密度は、図\(\PageIndex{1}\)に示すように、等高線マップでも表すことができます。

確率密度は、\(\PageIndex{1}\)で表されます。図\(\PageIndex{1}\)：水素原子の\(2p_x\)と\(3p_x\)軌道のX-y平面内の等高線プロット。\(\PageIndex{1}\)と\(\PageIndex{1}\)の間の距離を計算します。\(\PageIndex{1}\)と\(\PageIndex{1}\)の間の距離を計算します。\(\PageIndex{1}\)と\(\PageIndex{1}\)の間の距離を計算します。\(\PageIndex{1}\)と\(\PageIndex{1}\)の間の距離を計算します。\(\PageIndex{1}\)と\(\ 赤い線は高い\(R(r)r2\)のパスをたどり、低い\(R(r)r2\)の場合は青い線をたどります。 図を作成するために使用された角度関数は、2つの球面調和関数の線形結合でした（この章の最後にある問題10を参照してください。)

別の表現技術、仮想現実モデリングは、電子密度の表現のための約束の多くを保持しています。 たとえば、3次元空間を移動するワンドの力または抵抗として電子密度を体験できると想像してください。 触覚デバイスと呼ばれるこれらのようなデバイスは、すでに存在し、科学的情報を表現するために使用されています。 同様に、原子軌道を「飛行」し、色の変化や白濁の変化に応じて電子密度の変化を経験することは興味深いことではないでしょうか？ このような感覚を体験できるように、3Dスクリーンと視聴者の視線の方向についてのフィードバックを提供する”スマート”メガネを備えた特別に設計された部屋が現在開発されている。

原子軌道の半径部分を別々に調べる方法は、軌道内の電荷密度の分布に関する有用な情報を提供する。 図\(\PageIndex{2}\)にプロットされた1s、2s、および2p軌道に対する動径関数\(R(r)\)のグラフ。P>

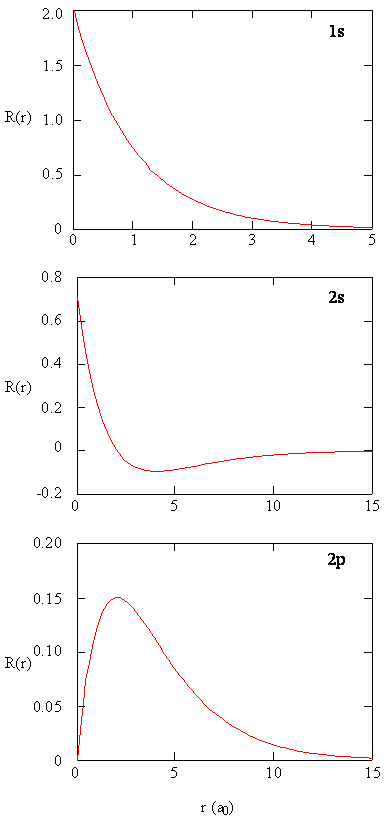
図\(\PageIndex{2}\)の1s関数は、核で高い正の値で始まり、5ボーア半径の後に指数関数的に本質的にゼロに減衰します。 核での高い値は驚くべきことかもしれませんが、後で見るように、核で電子を見つける確率は消えてしまいます。

次に、2s軌道の動径関数Figure\(\PageIndex{2}\)がゼロになり、負になることに注意してください。 この動作は、関数内に放射状ノードが存在することを明らかにします。 ラジアルノードは、ラジアル関数が\(r=0\)または\(r=∞\)以外のゼロに等しい場合に発生します。 原子軌道関数のノードと限界挙動は、どちらの軌道がどの波動関数によって記述されているかを識別するのに有用である。 たとえば、すべてのs関数は\(r=0\)で非ゼロの波動関数値を持ちますが、p、d、fおよび他のすべての関数は原点でゼロになります。 波動関数には\(n-1-l\)放射状ノードがあり、1s軌道には放射状ノードがなく、2sには放射状ノードが1つあるなどということを覚えておくと便利です。Exercise\(\PageIndex{5}\)

半径方向の波動関数の数学的な形を調べます。 関数のどのような機能により、それらのいくつかは原点でゼロになりますが、s関数は原点でゼロになりませんか？運動\(\PageIndex{6}\)

各放射状関数のどの数学的特徴が放射状ノードの数を制御しますか？運動\(\PageIndex{7}\)

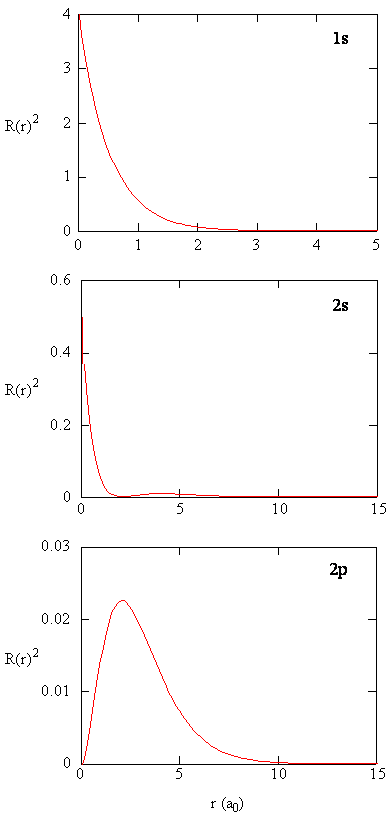
rのどの値で2sラジアルノードが発生しますか？N=1、2、および3の各関数のエネルギー、放射状ノードの数、角度ノードの数、ノードの合計数を提供するテーブルを作成します。 エネルギーとノードの数との関係を特定します。 放射状ノードの数と角度ノードの数との関係を特定します。量\(R(r)**R(r)\)は半径方向の確率密度、すなわち陽子からの距離\(r\)に位置する点に電子が存在する確率密度を与えます。\(r\)が存在しない場合、\(r\)が存在しない場合、\(r\)が存在しない場合、\(r\)が存在しない場合、\(r\)が存在しない場合、\(r\)が存在しない場合、\(r\)は存在しない。 3種類の原子軌道の半径方向の確率密度を図(\PageIndex{3}\)にプロットします。p>

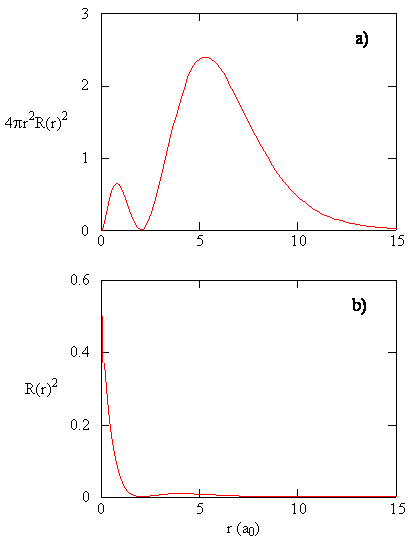
rのすべての値の半径方向の確率密度に、rのその特定の値で表される球面の面積を乗算すると、半径方向分布関数が得られます。 動径分布関数は、陽子からの距離rに位置する球の表面上の任意の場所に電子が見つかる確率密度を与えます。 球面の面積は\(4\pi r^2\)なので、動径分布関数は\(4\pi r^2R(r)**R(r)\)で与えられます。動径分布関数は、図\(\PageIndex{4}\)に示されています。 Ｒの小さい値では，半径の小さい表面積が核近傍の半径方向確率密度関数の高い値を変調するため，半径方向分布関数は低い。 \(R\)を増加させると、rの与えられた値に関連付けられた表面積が増加し、\(r^2\)項は、半径方向の確率密度が減少し始めているにもかかわらず、半径方向の分布関数を増加させます。\(r^2\)項は、半径方向の確率密度が減少し始めているにもかかわらず、半径方向の分布関数を増加させます。 \(R\)の値が大きい場合、動径関数の指数関数的減衰は、\(r^2\)項によって引き起こされる増加を上回り、動径分布関数は減少します。\(r^2\)の値は、\(r^2\)項によp>

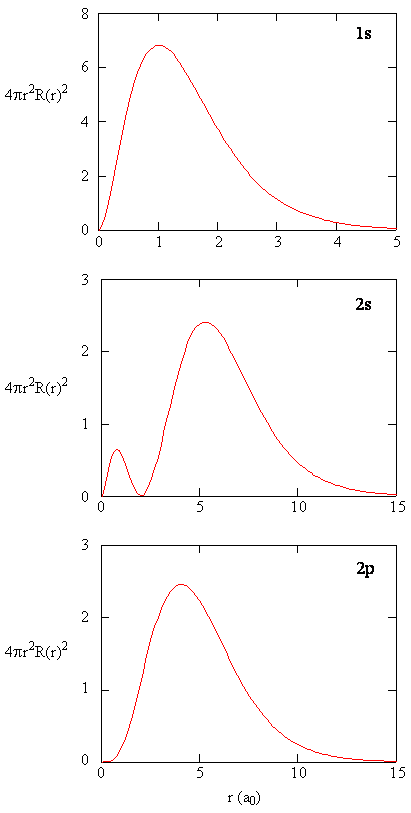
2s軌道の動径関数と動径分布関数の品質比較を記述します。

2s軌道の動径関数と動径分布関数の品質比較を記述します。

2s軌道の動径分布関数と動径分布関数の品質比較を記述します。 Figure(\PageIndex{5}\)を参照してください