breking, of buiging van licht, vindt plaats als licht van het ene medium naar het andere gaat met een andere brekingsindex. Breking is een belangrijk kenmerk van lenzen, waardoor ze een lichtbundel op een enkel punt kunnen richten, en is ook verantwoordelijk voor een verscheidenheid aan bekende verschijnselen, zoals de schijnbare vervorming van objecten die gedeeltelijk ondergedompeld zijn in water.

brekingsindex wordt gedefinieerd als de relatieve snelheid waarmee licht door een materiaal beweegt ten opzichte van zijn snelheid in een vacuüm. Volgens afspraak wordt de brekingsindex van een vacuüm gedefinieerd als een waarde van 1,0. De brekingsindex, n, van andere transparante materialen wordt gedefinieerd met de vergelijking:

waarbij c de lichtsnelheid en v de lichtsnelheid van dat materiaal is. Aangezien de brekingsindex van een vacuüm wordt gedefinieerd als 1.0 en een vacuüm is verstoken van enig materiaal, de brekingsindices van alle transparante materialen zijn daarom groter dan 1,0. Voor de meeste praktische doeleinden kan de brekingsindex van licht door lucht (1.0003) worden gebruikt om brekingsindices van onbekende materialen te berekenen. Brekingsindices van enkele veelvoorkomende materialen worden weergegeven in Tabel 1 hieronder.

materiaal brekingsindex lucht 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. Bijvoorbeeld, wanneer licht van een minder dichte medium, zoals lucht, naar een meer dichte medium, zoals water, De snelheid waarmee de elektromagnetische golf reist afneemt. Als alternatief, wanneer het licht van een meer dicht medium naar een minder dicht medium gaat, neemt de snelheid van de Golf toe.

de hoek waaronder gebroken licht zich verplaatst, is echter afhankelijk van zowel de invalshoek als de samenstelling van het materiaal waarin het binnenkomt. De norm kan worden gedefinieerd als een lijn loodrecht op de grens tussen twee stoffen. Licht gaat onder een hoek naar de normale grens en wordt gebroken volgens de wet van Snell:

waarbij n de brekingsindices van materiaal 1 en materiaal 2 voorstelt en q de hoeken van licht die door deze materialen reizen ten opzichte van de normale waarde symboliseert. Er zijn verschillende belangrijke punten die uit deze vergelijking kunnen worden getrokken. Wanneer n(1) groter is dan n (2), is de brekingshoek altijd kleiner dan de invalshoek. Als n(2) groter is dan n(1) is de brekingshoek ook altijd groter dan de invalshoek. Wanneer de twee brekingsindices gelijk zijn (n (1) = n (2)), dan wordt het licht doorgelaten zonder breking.

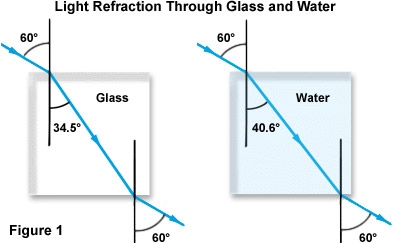
Het begrip brekingsindex wordt geïllustreerd in Figuur 1 hieronder, waarbij de nadruk ligt op het geval van licht dat uit de lucht door glas en water stroomt. Merk op dat, terwijl beide bundels het dichtere materiaal binnenkomen via dezelfde invalshoek ten opzichte van de normale (60 graden), de breking voor glas bijna 6 graden groter is dan die voor water als gevolg van de hogere brekingsindex van glas.

wetenschappers hebben vastgesteld dat de brekingsindex varieert met de frequentie van de straling (of golflengte) van licht. Dit verschijnsel komt samen met alle transparante media voor en wordt dispersie genoemd. Daarom moet bij het meten van de brekingsindex van een transparante stof de bij de meting gebruikte golflengte worden geïdentificeerd. Onderstaande tabel 2 geeft een overzicht van de verspreiding van drie onafhankelijke golflengten in verschillende media.

Materiaal Blauw (486.1 nm) Geel (589.3 nm) Rood (656.3 nm) Crown Glas 1.524 1.517 1.515 Flint Glas 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Dit licht wordt het D-lijnspectrum genoemd, en vertegenwoordigt het gele licht dat in Tabel 2 hierboven wordt vermeld. De spectra van de F-lijn en de C-lijn komen overeen met blauw en rood licht van specifieke golflengten die door waterstof worden uitgezonden. Deze spectra zijn fundamenteel voor de berekening van de dispersie, die kwantitatief kan worden gedefinieerd als:

waarbij n de brekingsindex is van het materiaal bij een bepaalde golflengte aangeduid door D, F en C, die de spectraallijnen van natrium en waterstof vertegenwoordigen zoals hierboven besproken. De relatie is zodanig dat als de golflengte van licht toeneemt, de brekingsindex afneemt. Veel factoren spelen echter een rol bij de verspreiding van verschillende materialen, waaronder hun elementaire en moleculaire samenstelling. Verscheidene anorganische vaste stoffen, zoals chromaten, dichromaten, cyaniden, vanadaten en halogenidecomplexen, hebben ongewoon hoge dispersies. Toch kunnen organische substituenten ook bijdragen aan een hoge dispersie.

	Interactive Java Tutorial
lichtbreking ontdek hoe de golflengte en invallende hoek van licht de breking beïnvloedt in verschillende mediums met verschillende brekingsindices.

Refraction of light is particularly important in the construction and physics of lenses. Vergeet niet, dat wanneer de lichtbundel zowel het glas als het water in Figuur 1 verliet, het opnieuw werd gebroken onder dezelfde hoek waaronder het het materiaal binnenkwam. Dit concept is essentieel voor het functioneren van lenzen, hoewel de vorm van de lens het resulterende beeld aanzienlijk beïnvloedt. In een convexe lens, zoals hieronder afgebeeld in Figuur 2, lichtgolven gereflecteerd door het object, in dit geval een giraffe, zijn gebogen naar het optische centrum van de lens en convergeren op het brandpunt.

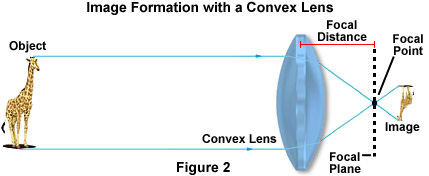
De relatieve positie van het object ten opzichte van het voorste brandpunt van de lens bepaalt hoe het object wordt afgebeeld. Als het object groter is dan tweemaal de lengte van het brandpunt, dan lijkt het kleiner en omgekeerd en moet worden afgebeeld door een extra lens om de grootte te vergroten. Wanneer het beeld echter dichter bij de lens staat dan het brandpunt, lijkt het beeld rechtop en groter, zoals met een eenvoudig vergrootglas gemakkelijk kan worden aangetoond.

	Interactive Java Tutorial
beeldvergroting onderzoek hoe het beeld van een giraffe wordt vergroot door breking van lichtgolven door een eenvoudige dunne bi-convexe lens.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. Een eenvoudig rietje in een met water gevuld glas, zoals afgebeeld in Figuur 3, is hiervan een goed voorbeeld. In dit voorbeeld moeten lichtgolven eerst door het water, dan door de glas/watergrens en uiteindelijk door de lucht. De lichtgolven gereflecteerd van de uiteinden van het stro zijn gebroken in een grotere mate dan die uit het midden van het stro, waardoor het stro lijkt vergroot en licht vervormd.

hetzelfde verschijnsel kan worden gebruikt om de brekingsindex van een vloeistof met een optische microscoop te bepalen. Om dit te doen, moet een vlakke cel die vloeistof met een merkteken (of schaalverdelingen) kan vasthouden worden geplaatst op de binnenkant van het glasoppervlak. Ook moet een van de oculairs van de microscoop een gegradueerd netvlies hebben ingebracht op het primaire beeldvlak voor lijnbreedtemetingen van de markering in de platte cel. Alvorens de vloeistof van onbekende brekingsindex aan de cel toe te voegen, zou de microscoop op het teken bij de bodem van de cel en een meting van de positie van het teken op het opgemerkt netvlies moeten worden geconcentreerd. Vervolgens moet een kleine hoeveelheid vloeistof worden toegevoegd aan de cel en de microscoop opnieuw gericht op het teken (door de vloeistof) en een nieuwe meting worden uitgevoerd. De microscoop moet dan eindelijk worden gericht op het oppervlak van de vloeistof, en een derde lezing geregistreerd door het meten van de positie van de markering op het netvlies. De brekingsindex van de onbekende vloeistof kan vervolgens worden berekend met behulp van de volgende vergelijking:

waarbij D(gemeten) de gemeten diepte is (van het vloeistofoppervlak tot de positie van de markering op de lege cel) met behulp van de microscoop en D(schijnbaar) de tekenmeting met en zonder vloeistof.

de kritische reflectiehoek is een ander sleutelbegrip in de studie van de lichtbreking en wordt hieronder in Figuur 4 geïllustreerd. Wanneer het licht door een medium van hoge brekingsindex in een medium van lagere brekingsindex gaat, wordt de invallende hoek van de lichtgolven een belangrijke factor. Als de invallende hoek voorbij een specifieke waarde toeneemt (afhankelijk van de brekingsindex van de twee media), zal het een punt bereiken waar de hoek zo groot is dat er geen licht wordt gebroken in het medium met een lagere brekingsindex.

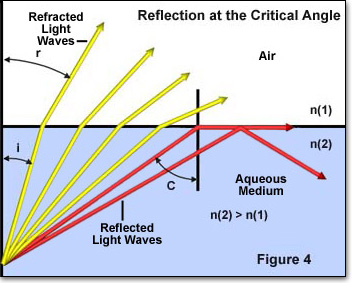
in Figuur 4 worden individuele lichtstralen weergegeven door rode of gele pijlen die zich verplaatsen van een medium met een hoge brekingsindex (n(2)) naar een middel met een lagere brekingsindex (n(1)). De invalshoek van elke individuele lichtstraal wordt aangeduid door i en de brekingshoek door r. De vier gele lichtstralen hebben allemaal een invalshoek (i) die laag genoeg is om door het raakvlak tussen de twee media te gaan. De twee rode lichtstralen hebben echter invallende hoeken die de kritische hoek (ongeveer 41 graden) overschrijden en worden gereflecteerd in de grens tussen de media of terug in het medium met hoge brekingsindex. Dit verschijnsel vindt plaats wanneer de brekingshoek (hoek r in Figuur 4) gelijk wordt aan 90 graden en de wet van Snell vermindert tot:

waarbij (q) nu de kritische hoek wordt genoemd C. Als het medium van de lagere brekingsindex lucht is (n = 1,00), vermindert de vergelijking verder tot:

zoals eerder besproken, is een ander belangrijk kenmerk van lichtbreking dat de golflengte van licht een invloed heeft op de hoeveelheid lichtbreking die optreedt in een medium. In feite is de hoeveelheid breking die plaatsvindt omgekeerd evenredig met de golflengte van het invallende licht. Aldus, wordt het kortere golflengte zichtbare licht gebroken onder een grotere hoek dan het langere golflengtelicht. Bijgevolg, wanneer wit licht, dat is samengesteld uit Alle kleuren in het zichtbare spectrum, wordt doorgegeven door een glazen prisma, wordt het verspreid in de samenstellende kleuren op een manier die afhankelijk is van de individuele golflengten. Laagfrequent zichtbaar licht (600 nanometer en groter) wordt gebroken onder een kleinere hoek dan hogerfrequent licht, wat resulteert in een regenboog-achtig effect, zoals hieronder afgebeeld in Figuur 5.

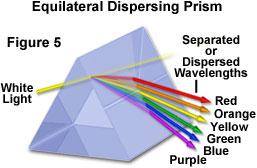
dit zelfde fenomeen is ook verantwoordelijk voor chromatische aberratie. Wanneer het witte licht door een eenvoudige bolle lens wordt overgegaan, ontstaan verscheidene brandpuntspunten in dichte nabijheid die aan de kleine brekingsindexverschillen van de componentgolflengten beantwoorden. Dit effect heeft de neiging om gekleurde (of rood of blauw, afhankelijk van de focus) halo ‘ s rond de beelden van objecten te produceren. De correctie van deze aberratie wordt gewoonlijk bereikt door het gebruik van combinaties van twee of meer lenselementen die bestaan uit materialen met verschillende dispersieve eigenschappen, zoals een achromatische lens die is geconstrueerd met zowel kroon-als flintglazen.

	Interactive Java Tutorial
refractie door een prisma onderzoek hoe wit licht wordt gescheiden in de samenstellende kleuren door refractie door verschillende hoeken in een prisma.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. Het meest voorkomende voorbeeld is een camera, die is ontworpen om scherpe en gerichte beelden te maken op een emulsie van film of het oppervlak van een charge-coupled device (CCD) om een nauwkeurig beeld te produceren. Andere optische apparaten die deze kenmerken van licht exploiteren omvatten microscopen en telescopen, die het mogelijk maken het bekijken van objecten die onzichtbaar zijn voor het menselijke oog zonder hulp, ongeacht of ze zich op het hoofd van een pin of in een ver sterrenstelsel bevinden.

bijdragende auteurs

Mortimer Abramowitz – Olympus America, Inc. Twee Corporate Center Drive. Melville, New York, 11747.Shannon H. Neaves and Michael W. Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., the Florida State University, Tallahassee, Florida, 32310.

BACK TO LIGHT AND COLOR

vragen of opmerkingen? Stuur ons een email.

© 1998-2021 door Michael W. Davidson en de Florida State University. Alle Rechten Voorbehouden. Geen afbeeldingen, afbeeldingen, scripts of applets mogen worden gereproduceerd of gebruikt op welke manier dan ook zonder toestemming van de houders van het auteursrecht. Gebruik van deze website betekent dat u akkoord gaat met alle van de wettelijke voorwaarden die door de eigenaren.

deze website wordt onderhouden door ons
Graphics & Web Programming Team
In samenwerking met optische microscopie van het
National High Magnetic Field Laboratory.

laatste wijziging: vrijdag 13 Nov 2015 om 14: 18

Aantal toegang sinds 10 maart 2003:181405

bezoek de websites van onze partners in het onderwijs: