8.2 :Wavefunctions
løsningene til hydrogenatomet Schrö ligningen er funksjoner som er produkter av en sfærisk harmonisk funksjon og en radial funksjon.bølgefunksjonene for hydrogenatomet avhenger av de tre variablene r, \(\theta\) og \(\varphi \) og de tre kvantetallene n, \(l\) og \(m_l\). Variablene gir posisjonen til elektronen i forhold til protonen i sfæriske koordinater. Den absolutte kvadratet av bølgefunksjonen, \(| \psi (r, \theta , \varphi )|^2\), evaluert ved \(r\), \(\theta\) og \(\varphi\) gir sannsynlighetstettheten for å finne elektronen inne i et differensialvolum \(d \ tau\), sentrert ved posisjonen spesifisert av r, \(\theta\) og \ (\varphi\).
Øvelse \(\PageIndex{1}\)
hva er verdien av integralet
\
kvante tallene har navn: \(n\) kalles hovedkvantumnummeret, \(l\) kalles vinkelmomentkvantumnummeret, og \(m_l\) kalles magnetisk kvantumnummer fordi (som vi vil se i Avsnitt 8.4) energien i et magnetfelt avhenger av \(m_l\). Ofte kalles \(l\) det azimutale kvantetallet fordi det er en konsekvens av \(\theta\)-ligningen, som involverer den azimutale vinkelen \(\Theta\), og refererer til vinkelen til senit.
disse kvantetallene har spesifikke verdier som dikteres av de fysiske begrensningene eller grensebetingelsene som er pålagt schrö-ligningen: \(n\) må være et heltall større enn 0, \(l\) kan ha verdiene 0 til n‑1, og \(m_l\) kan ha \(2l + 1\) verdier fra \(-l\) ‑ til \(+l\) i enhet eller heltallstrinn. Verdiene av kvantetallet \(l\) er vanligvis kodet med et brev: s betyr 0, p betyr 1, d betyr 2, f betyr 3; de neste kodene fortsetter alfabetisk (f.eks. Kvantumnumrene angir kvantisering av fysiske mengder. De diskrete energiene til forskjellige tilstander av hydrogenatomet er gitt av \(n\), størrelsen på vinkelmomentet er gitt av \(l\), og en komponent av vinkelmomentet(vanligvis valgt av kjemikere å være z‑komponenten) er gitt av \(m_l\). Det totale antall orbitaler med en bestemt verdi av \(n\) er \(n^2\).
Øvelse \(\PageIndex{2}\)
Vurder flere verdier for n, og vis at antall orbitaler for hver n er \(n^2\).
Øvelse \(\PageIndex{3}\)
Konstruer en tabell som oppsummerer de tillatte verdiene for kvante tallene n, \(l\) og \(M_l\). for energinivå 1 til 7 av hydrogen.
Øvelse \(\PageIndex{4}\)
notasjonen 3d angir kvante tallene for et elektron i hydrogenatomet. Hva er verdiene for n og \ (l\)? Hva er verdiene for energi og vinkelmoment? Hva er de mulige verdiene for det magnetiske kvantetallet? Hva er de mulige orienteringene for vinkelmomentvektoren?
hydrogenatombølgefunksjonene, \(\psi (r, \theta, \ varphi)\), kalles atomorbitaler. En atom orbital er en funksjon som beskriver en elektron i et atom. Bølgefunksjonen med n = 1, \(l=1\) og\ (m_l\) = 0 kalles 1s-orbitalet, og et elektron som er beskrevet av denne funksjonen sies å være » i » ls-orbitalet, dvs. har en 1s-orbitaltilstand. Begrensningene på \(n\), \(l)\) og \ (m_l\) som pålegges under løsningen Av hydrogenatomet Schr ③dinger-ligningen, forklarer hvorfor det er en enkelt 1s-orbital, hvorfor det er tre 2p-orbitaler, fem 3d-orbitaler, etc. Vi vil se når vi vurderer multi-elektronatomer I Kapittel 9 at disse begrensningene forklarer funksjonene i Det Periodiske Bordet. Periodisk Tabell er med Andre ord en manifestasjon Av Schrö-modellen og de fysiske begrensningene som er pålagt å oppnå løsningene Til Schrö-ligningen for hydrogenatomet.Visualisering av variasjonen av en elektronisk bølgefunksjon med \(r\), \(\theta\) og \(\varphi\) er viktig fordi det absolutte kvadratet av bølgefunksjonen skildrer ladningsfordelingen (elektronsannsynlighetstetthet) i et atom eller molekyl. Ladningsfordelingen er sentral for kjemi fordi den er relatert til kjemisk reaktivitet. For eksempel tiltrekkes en elektron mangelfull del av ett molekyl til en elektron rik region av et annet molekyl, og slike interaksjoner spiller en viktig rolle i kjemiske interaksjoner som spenner fra substitusjons-og addisjonsreaksjoner til proteinfolding og samspillet mellom substrater og enzymer.Visualisering av bølgefunksjoner og ladefordelinger er utfordrende fordi det krever å undersøke oppførselen til en funksjon av tre variabler i tredimensjonalt rom. Denne visualiseringen gjøres lettere ved å vurdere de radiale og vinkeldelene separat, men å plotte de radiale og vinkeldelene separat avslører ikke formen på en orbital veldig bra. Formen kan avsløres bedre i en sannsynlighetstetthetsplott. For å lage et slikt tredimensjonalt plott, dele rom opp i små volumelementer, beregne \(\psi^ * \ psi \) i midten av hvert volumelement, og deretter skygge, stipple eller farge det volumelementet i forhold til størrelsen på \(\psi^* \ psi \). Ikke forveksle slike tomter med polare tomter, som ser like ut.
Sannsynlighetstettheter kan også representeres av konturkart, som vist I Figur \(\PageIndex{1}\).
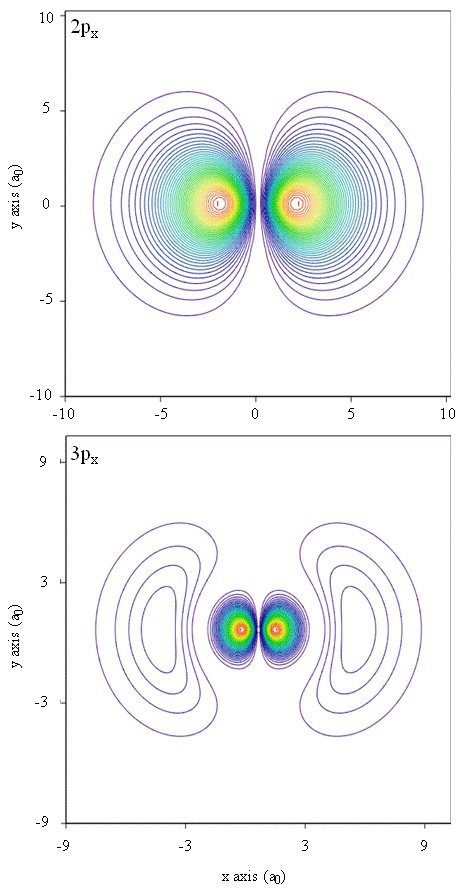
En annen representasjonsteknikk, virtuell virkelighetsmodellering, har mye løfte om representasjon av elektrondensiteter. Tenk deg for eksempel å kunne oppleve elektrontetthet som en kraft eller motstand på en tryllestav som du beveger deg gjennom tredimensjonalt rom. Enheter som disse, kalt haptiske enheter, eksisterer allerede og brukes til å representere vitenskapelig informasjon. På samme måte ville det ikke være interessant å » fly » gjennom en atombane og oppleve endringer i elektrondensitet som fargeendringer eller skyhet endres? Spesialdesignede rom MED 3D-skjermer og» smarte » briller som gir tilbakemelding om retningen til betrakterens blikk, utvikles for å tillate oss å oppleve slike opplevelser.Metoder for separat undersøkelse av de radiale delene av atomorbitaler gir nyttig informasjon om fordelingen av ladningstettheten i orbitalene. Grafer av de radiale funksjonene, \(R(r)\), for 1s, 2s og 2p orbitaler plottet I Figur \(\PageIndex{2}\).
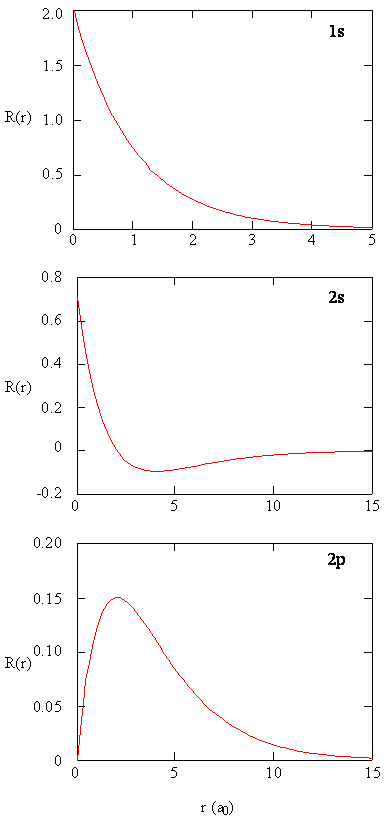
1s-funksjonen I Figur \(\PageIndex{2}\) starter med en høy positiv verdi ved kjernen og eksponentielt henfaller til i det vesentlige null etter 5 Bohr-radier. Den høye verdien i kjernen kan være overraskende, men som vi skal se senere, er sannsynligheten for å finne et elektron i kjernen forsvinnende liten.
neste legg merke til hvordan radialfunksjonen for 2s-orbitalet, Figur \(\PageIndex{2}\), går til null og blir negativ. Denne oppførselen avslører tilstedeværelsen av en radial knute i funksjonen. En radial node oppstår når radialfunksjonen er lik null annet enn ved \(r = 0\) eller \(r = ∞\). Noder og begrensende oppførsel av atomorbitale funksjoner er begge nyttige for å identifisere hvilken orbital som beskrives ved hvilken bølgefunksjon. For eksempel har alle s-funksjonene ikke-null bølgefunksjonsverdier ved \(r = 0\), men p, d, f og alle andre funksjoner går til null ved opprinnelsen. Det er nyttig å huske at det er \(n-1-l\) radiale noder i en bølgefunksjon, noe som betyr at en 1s-orbital ikke har radiale noder, en 2s har en radialnode og så videre.
Øvelse \(\PageIndex{5}\)
Undersøk matematiske former for radiale bølgefunksjoner. Hvilken funksjon i funksjonene får noen av dem til å gå til null ved opprinnelsen mens s-funksjonene ikke går til null ved opprinnelsen?
Øvelse \(\PageIndex{6}\)
hvilken matematisk funksjon av hver av de radiale funksjonene styrer antall radiale noder?
Øvelse \(\PageIndex{7}\)
ved hvilken verdi av r forekommer 2s radial node?
Øvelse \(\PageIndex{8}\)
Lag et bord som gir energi, antall radiale noder og antall vinkelnoder og totalt antall noder for hver funksjon med n = 1, 2 og 3. Identifiser forholdet mellom energi og antall noder. Identifiser forholdet mellom antall radiale noder og antall vinkelnoder.
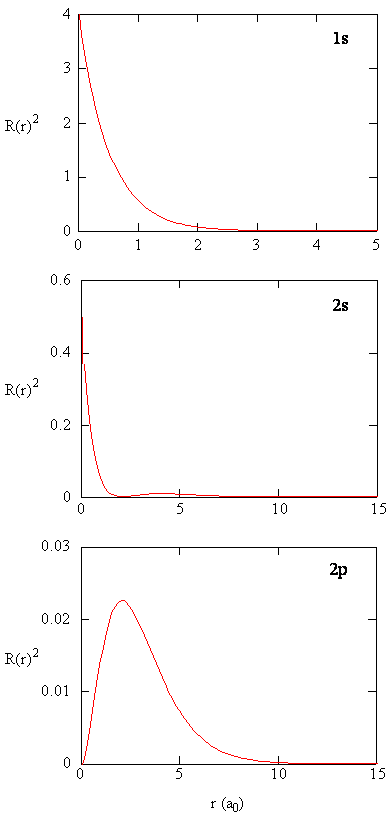
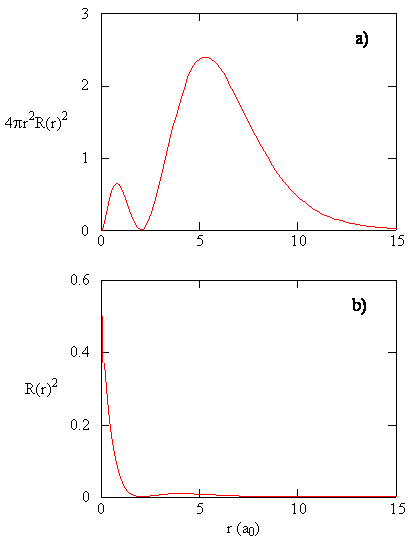
mengden \(R (r) ^* R(r)\) gir den radiale sannsynlighetstettheten; dvs. sannsynlighetstettheten for elektronen å være på et punkt som ligger avstanden \(r\) fra protonen. Radial sannsynlighetstettheter for tre typer atomorbitaler er plottet I Figur (\PageIndex{3}\).
når den radiale sannsynlighetstettheten for hver verdi av r multipliseres med arealet av den sfæriske overflaten representert ved den spesielle verdien av r, får vi radialfordelingsfunksjonen. Radialfordelingsfunksjonen gir sannsynlighetstettheten for et elektron som finnes hvor som helst på overflaten av en sfære som ligger en avstand r fra protonet. Siden arealet av en sfærisk overflate er \(4 \ pi r^2\), er den radiale fordelingsfunksjonen gitt av \(4 \pi r^2 R(r) ^ * R (r)\).
Radialfordelingsfunksjoner er vist I Figur \(\PageIndex{4}\). Ved små verdier av r er den radiale fordelingsfunksjonen lav fordi det lille overflatearealet for små radier modulerer den høye verdien av den radiale sannsynlighetstetthetsfunksjonen nær kjernen. Når vi øker \(r\), øker overflatearealet forbundet med en gitt verdi av r, og \(r^2\) termen fører til at radialfordelingsfunksjonen øker selv om den radiale sannsynlighetstettheten begynner å synke. Ved store verdier av \(r\) oppveier eksponentiell forfall av radialfunksjonen økningen forårsaket av \(r^2\) termen og radialfordelingsfunksjonen minker.
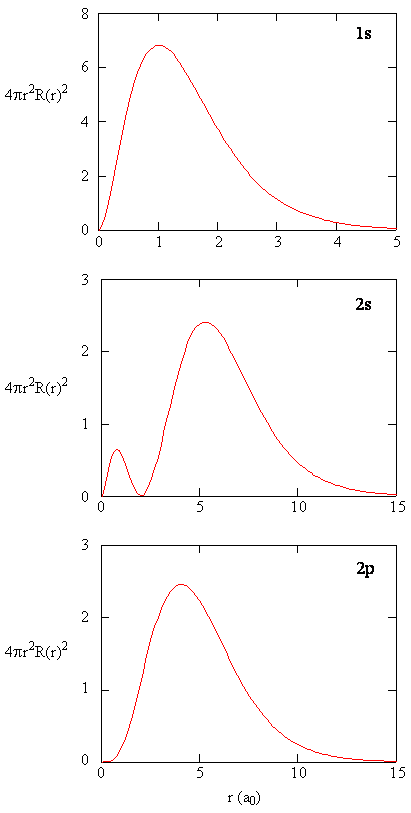
Øvelse \(\PageIndex{9}\)
Skriv en kvalitetssammenligning av radialfunksjonen og radialfordelingsfunksjonen for 2s-orbitalet. Se Figur (\PageIndex{5}\)
Bidragsytere og Attribusjoner
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski («Kvantetilstander Av Atomer og Molekyler»)