Blog
I et tidligere blogginnlegg diskuterte vi hvordan supermarkeder bruker data for å bedre forstå forbrukernes behov og til slutt øke deres totale forbruk. En av de viktigste teknikkene som brukes av de store forhandlerne kalles Market Basket Analysis (MBA), som avdekker foreninger mellom produkter ved å se etter kombinasjoner av produkter som ofte forekommer i transaksjoner. Med andre ord, det tillater supermarkeder å identifisere relasjoner mellom produktene som folk kjøper. For eksempel vil kunder som kjøper blyant og papir, sannsynligvis kjøpe gummi eller linjal.
«Markedskurvanalyse lar forhandlere identifisere relasjoner mellom produktene som folk kjøper.»
Forhandlere kan bruke innsiktene fra MBA på en rekke måter, inkludert:
- Gruppering av produkter som forekommer i utformingen av butikkens layout for å øke sjansen for kryssalg;
- Kjører anbefalingsmotorer på nettet («kunder som kjøpte dette produktet så også på dette produktet»); Og
- Målretting av markedsføringskampanjer ved å sende ut kampanjekuponger til kunder for produkter relatert til varer de nylig har kjøpt.Gitt hvor populær OG verdifull MBA er, trodde vi at vi skulle produsere følgende trinnvise veiledning som beskriver hvordan det fungerer og hvordan du kan gå om å gjennomføre din Egen Markedskurvanalyse.
Hvordan Markedet Kurv Analyse arbeid?
for Å gjennomføre EN MBA trenger du først et datasett av transaksjoner. Hver transaksjon representerer en gruppe varer eller produkter som er kjøpt sammen og ofte referert til som en «itemset». For eksempel kan ett elementsett være: {blyant, papir, stifter, gummi} i så fall har alle disse elementene blitt kjøpt i en enkelt transaksjon.
i EN MBA analyseres transaksjonene for å identifisere foreningsregler. For eksempel kan en regel være: {blyant, papir} = > {rubber}. Dette betyr at hvis en kunde har en transaksjon som inneholder blyant og papir, vil de sannsynligvis også være interessert i å kjøpe en gummi.
før du handler etter en regel, må en forhandler vite om det er tilstrekkelig bevis for at det vil resultere i et gunstig utfall. Vi måler derfor styrken til en regel ved å beregne følgende tre beregninger (merk at andre beregninger er tilgjengelige, men disse er de tre mest brukte):
Støtte: prosentandelen av transaksjoner som inneholder alle elementene i et elementsett(f. eks. blyant, papir og gummi). Jo høyere støtte jo oftere oppstår itemset. Regler med høy støtte foretrekkes siden de sannsynligvis vil gjelde for et stort antall fremtidige transaksjoner.
Konfidens: sannsynligheten for at en transaksjon som inneholder elementene på venstre side av regelen (i vårt eksempel, blyant og papir) også inneholder elementet på høyre side (en gummi). Jo høyere tillit, jo større er sannsynligheten for at varen på høyre side vil bli kjøpt eller, med andre ord, jo større avkastning rate du kan forvente for en gitt regel.
Løft: sannsynligheten for at alle elementene i en regel forekommer sammen (ellers kjent som støtten) dividert med produktet av sannsynlighetene for elementene på venstre og høyre side som oppstår som om det ikke var noen sammenheng mellom dem. For eksempel, hvis blyant, papir og gummi skjedde sammen i 2,5% av alle transaksjoner, blyant og papir i 10% av transaksjonene og gummi i 8% av transaksjonene, ville heisen være: 0.025/(0.1*0.08) = 3.125. Et løft på mer enn 1 antyder at tilstedeværelsen av blyant og papir øker sannsynligheten for at en gummi også vil forekomme i transaksjonen. Samlet sett oppsummerer lift styrken av foreningen mellom produktene på venstre og høyre side av regelen; jo større heisen jo større koblingen mellom de to produktene.For å utføre En Markedskurvanalyse og identifisere potensielle regler, brukes en data mining algoritme kalt ‘Apriori-algoritmen’ ofte, som fungerer I to trinn: Systematisk identifisere itemsets Som forekommer ofte i datasettet med en støtte som er større enn en forhåndsdefinert terskel.
- Beregn tilliten til alle mulige regler gitt de hyppige itemsets og hold bare de med en tillit større enn en forhåndsdefinert terskel.
tersklene for å angi støtte og tillit er brukerdefinert og vil sannsynligvis variere mellom transaksjonsdatasett. R har standardverdier, men vi anbefaler at du eksperimenterer med disse for å se hvordan de påvirker antall regler som returneres (mer om dette nedenfor). Til slutt, selv Om Apriori-algoritmen ikke bruker lift for å etablere regler, ser du i det følgende at vi bruker lift når vi utforsker reglene som algoritmen returnerer.
Utføre Markedskurvanalyse I R
for å demonstrere hvordan man skal utføre EN MBA har vi valgt Å bruke R og spesielt arules-pakken. For de som er interessert har vi tatt Med R-koden som vi brukte på slutten av denne bloggen.
her følger vi det samme eksemplet som brukes i arulesViz-Vignetten og bruker et datasett av dagligvaresalg som inneholder 9.835 individuelle transaksjoner med 169 varer. Det første vi gjør er å se på elementene i transaksjonene, og spesielt plotte den relative frekvensen av De 25 hyppigste elementene I Figur 1. Dette tilsvarer støtten til disse elementene der hvert elementsett bare inneholder det enkle elementet. Denne barplottet illustrerer dagligvarer som ofte kjøpes i denne butikken, og det er bemerkelsesverdig at støtten til selv de hyppigste varene er relativt lav (for eksempel forekommer det hyppigste elementet i bare rundt 2,5% av transaksjonene). Vi bruker disse innsiktene til å informere minimumsgrensen når Du kjører Apriori-algoritmen; for eksempel vet vi at for at algoritmen skal returnere et rimelig antall regler, må vi sette støttegrensen til godt under 0.025.
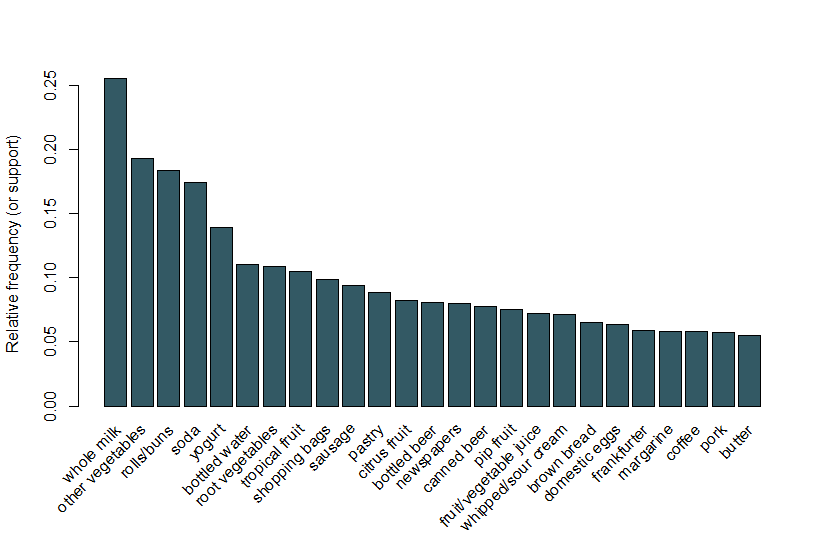
Figur 1 en bar plott av støtte av de 25 hyppigste varer kjøpt.
ved å sette en støtteterskel på 0,001 og tillit på 0,5, kan Vi kjøre Apriori-algoritmen og få et sett med 5,668-resultater. Disse terskelverdiene er valgt slik at antall returnerte regler er høyt, men dette tallet vil redusere hvis vi økte en terskel. Vi vil anbefale å eksperimentere med disse terskelene for å oppnå de mest hensiktsmessige verdiene. Mens det er for mange regler for å kunne se på dem alle individuelt, kan vi se på de fem reglene med den største heisen:
| Regel | Støtte | Tillit | Løft |
| {instant mat produkter,brus}=>{hamburger kjøtt} | 0.001 | 0.632 | 19.00 |
| {brus, popcorn}=>{salt snacks} | 0.001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. For eksempel kan den første regelen representere hva slags varer kjøpt for EN BBQ, den andre for en filmkveld og den tredje for baking.i Stedet for å bruke tersklene for å redusere reglene ned til et mindre sett, er det vanlig at et større sett med regler returneres slik at det er større sjanse for å generere relevante regler. Alternativt kan vi bruke visualiseringsteknikker for å inspisere regelsettet som returneres og identifisere de som sannsynligvis vil være nyttige.
Ved hjelp av arulesViz-pakken plotter vi reglene med tillit, støtte Og løft I Figur 2. Denne plottet illustrerer forholdet mellom de ulike beregningene. Det har vist seg at de optimale reglene er de som ligger på det som kalles «støtte-tillit grensen». I hovedsak er disse reglene som ligger på høyre kant av tomten der enten støtte, tillit eller begge er maksimert. Plottfunksjonen i arulesViz-pakken har en nyttig interaktiv funksjon som lar deg velge individuelle regler (ved å klikke på tilhørende datapunkt), noe som betyr at reglene på grensen lett kan identifiseres.
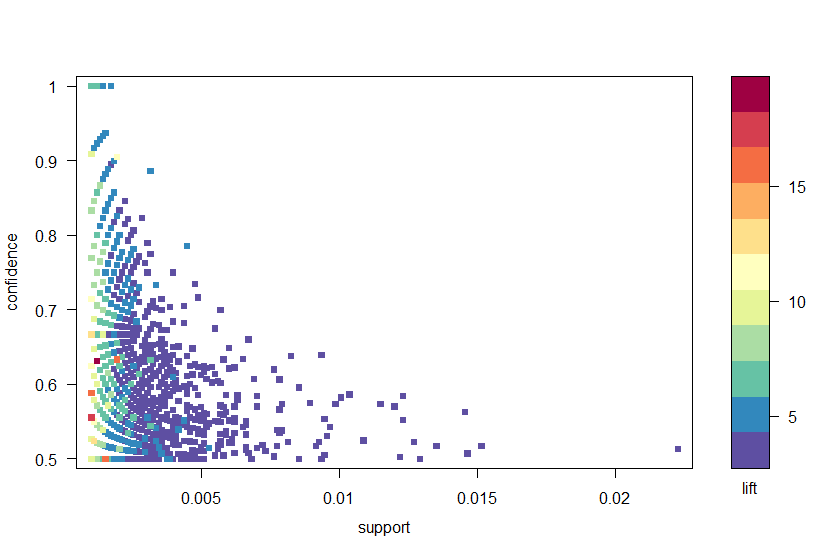
Figur 2: et spredningsplott av tillit, støtte og løfteverdier.
det er mange andre tomter tilgjengelig for å visualisere reglene, men en annen figur som vi vil anbefale å utforske er grafbasert visualisering (Se Figur 3) av de ti beste reglene når det gjelder løft (du kan inkludere mer enn ti, men disse typer grafer kan lett bli rotete). I denne grafen representerer elementene gruppert rundt en sirkel et elementsett og pilene angir forholdet i regler. For eksempel er en regel at kjøp av sukker er knyttet til kjøp av mel og bakepulver. Størrelsen på sirkelen representerer nivået av tillit knyttet til regelen og fargen løftnivået (jo større sirkelen og mørkere grå jo bedre).
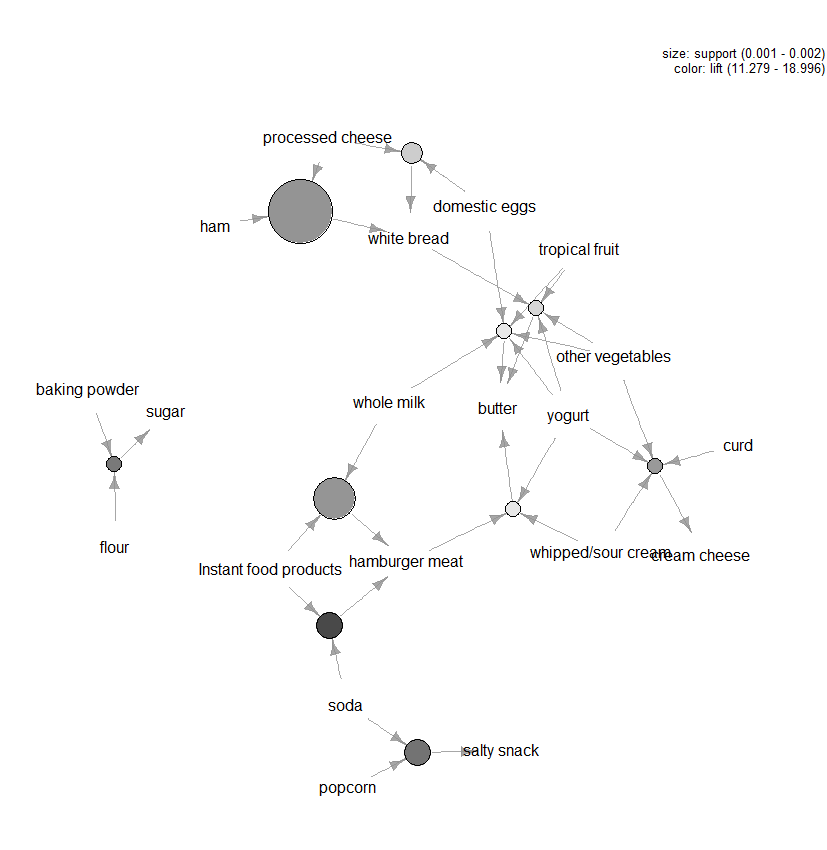
Figur 3: Grafbasert visualisering av de ti beste reglene når det gjelder løft.
Market Basket Analyse Er et nyttig verktøy for forhandlere som ønsker å bedre forstå forholdet mellom produktene som folk kjøper. DET er mange verktøy som kan brukes når du utfører MBA og de vanskeligste aspektene til analysen setter tillit og støtte terskler I Apriori algoritmen og identifisere hvilke regler er verdt å forfølge. Vanligvis gjøres sistnevnte ved å måle reglene i form av beregninger som oppsummerer hvor interessante de er, ved hjelp av visualiseringsteknikker og også mer formell multivariat statistikk. Til SLUTT er nøkkelen TIL MBA å trekke ut verdi fra transaksjonsdataene dine ved å bygge opp en forståelse av forbrukernes behov. Denne typen informasjon er uvurderlig hvis du er interessert i markedsføringsaktiviteter som kryssalg eller målrettede kampanjer.
hvis du vil vite mer om hvordan du analyserer transaksjonsdataene dine, kan du kontakte oss, så hjelper vi deg gjerne.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries)
LIST(Groceries)
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.