Den Revolusjonære Galois Teorien

Den 31. Mai 1832 døde en fransk Republikansk revolusjonær kalt É Galois av et skudd. Han var 20 år gammel. Natten før, fryktet Sin egen død, Hadde Galois skrevet mange brev, frenetisk skriblet «jeg har ingen tid; jeg har ingen tid». Et brev er spesielt verdifullt Av Historiske grunner. I dette brevet hevder Galois å ha utløst revolusjonen. Ikke politisk. En matematisk en.
Revolusjonen Galois initierte viste seg å være større og dypere enn han kunne ha forestilt seg det! Landskapet i matematikk har blitt dypt påvirket Av Galois ‘ visjon, som sin avkom har steget og tatt over den matematiske verden. Dette avkom er nå allestedsnærværende og regler grenseløse land. Det går under navnet ren algebra.
for å romantisere Enda litt mer historien Om Galois ‘ dramatiske liv, her er et sammendrag av en dokumentar jeg laget om algebra:

Han er definitivt! Men hans matematiske revolusjon gikk ikke jevnt. Som alle revolusjonsledere hadde han først de største vanskeligheter. Ikke for å forestille revolusjonen. Men for å overbevise andre om å bli med ham i en spillendrende tilnærming til matematikk. Da Galois fortsatt var i live, ble hans revolusjonerende ideer avvist flere ganger av det franske vitenskapsakademiet … fordi de beste franske matematikerne på den tiden Som Simé Denis Poisson bare ikke kunne få det! Delvis på Grunn Av Galois ‘ uleselige håndskrift vist til høyre …
Det var definitivt et stort løft. Men det ville ta ytterligere 82 år for Den Store Østerrikske matematikeren Emil Artin å endelig gi Galois-teorien sin moderne form, i 1942. Artin fortjener mange kreditter. Mens Galois var visjonær som forutså denne revolusjonen, Artin, i mange sanser, Er den som faktisk foretok revolusjonen og veltet matematikk. Takket Være Artin, og noen få andre, Har Galois-teorien i dag blitt en uunngåelig hjørnestein i forskning i matematikk, med mange overraskende og fantastiske prestasjoner (Som Wiles’ bevis på Fermats siste teorem), samt et stort reservoar av åpne spørsmål og mysterier!
Felt i Ren Algebra
Galois teori handler om symmetrier av tall. Men før jeg kommer dit, må jeg introdusere deg for å få deg bevæpnet ved å fortelle deg en hemmelighet om tall. Og jeg er sikker på at du har hørt om det! Faktisk, tilbake i videregående skole, ble du sannsynligvis lært å aldri forlate røtter i denominatorene.
jeg mener at $1 / (\sqrt{2}-1)$ ikke var et riktig svar. Kan du bidra til å kvitte seg med kvadratroten av 2 i nevnen?
Hehe … Vi ble lært å multiplisere opp og ned av nevnerens konjugat. Dette konjugatet oppnås ved å erstatte $ – $ med $ + $ (eller omvendt) i nevnen:
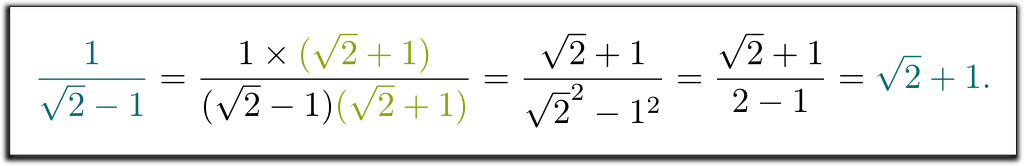
jeg vet! Det kompliserte uttrykket $1/(\sqrt{2}-1)$ representerer det samme tallet som $\sqrt{2} + 1$. Og dette forklarer hvorfor våre lærere ønsket at vi skulle skrive resultater på en måte i stedet for den andre: når alt er skrevet på samme måte, blir eksamener mye lettere å rette opp!
Men hva med $1 / (\sqrt{2}-1)$? Kan du bli kvitt roten i nevnen? Kan det til og med gjøres?
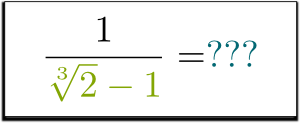
jeg vet!
du forteller meg!
Noe hell?
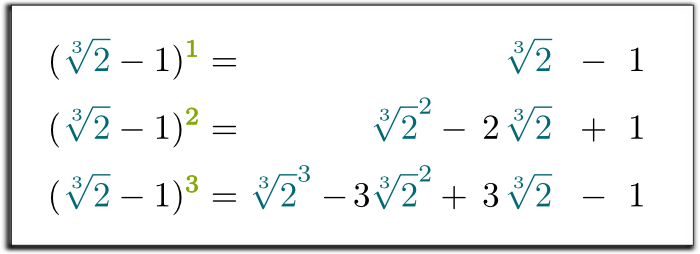
Ja det er det! Ved å gjøre denne substitusjonen i den tredje ligningen har vi vist at de tre første kreftene på $\sqrt{2}-1$ kan skrives som en sum av et rasjonelt tall, på $\sqrt{2}$ og $\sqrt{2}^2$!
Så vi har nå 3 ligninger, med 2 rotuttrykk vi vil bli kvitt! Dermed kan vi kombinere ligningene for å fjerne alle rotuttrykk til høyre!
la oss multiplisere de 2 første linjene med 3 og legge sammen alle 3 ligningene:
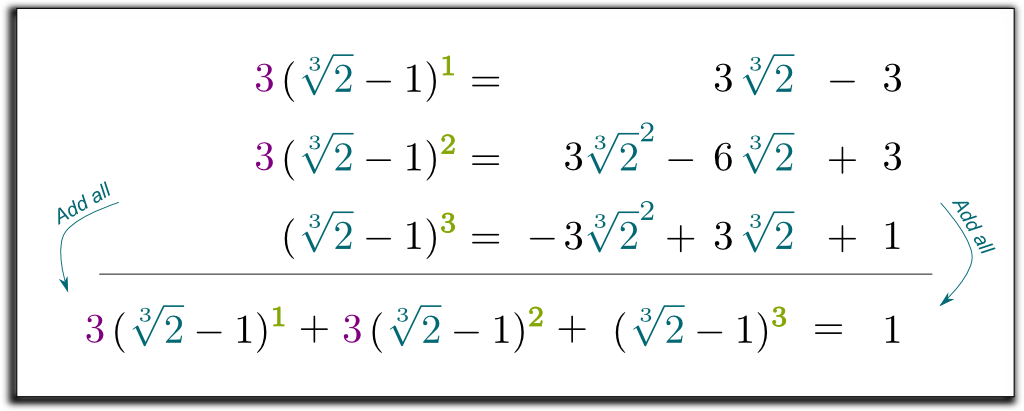
Hehe … den kule tingen er at venstre term vi har oppnådd nå kan faktoriseres av $\sqrt{2}-1$! La meg hoppe over noen kjedelige beregninger… og komme til resultatet $(\sqrt{2}-1)$ $(\sqrt{2}^2 + \sqrt{2} + 1)$ $= 1$. Så, for å kvitte seg med røttene i nevnen, kan vi multiplisere opp og ned med $\sqrt{2}^2 + \sqrt{2} + 1$! Til slutt får vi følgende overraskende og vakre formel:
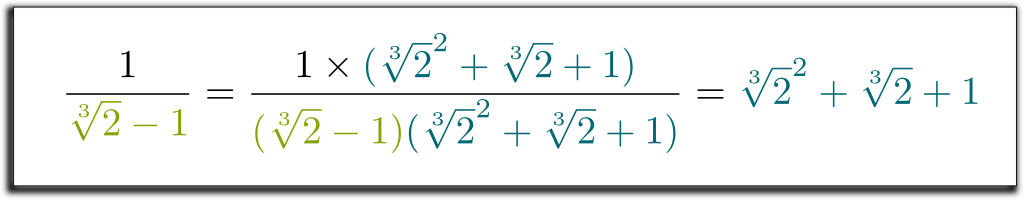
jeg vet! Men hva er enda penere er at metoden vi brukte er veldig generell! Med lignende teknikk kan vi nå fjerne alle radikaler fra denominatorer!
Nå var Det Av Spesiell interesse For Galois ikke det faktum at en metode gjorde det mulig å fjerne radikaler fra denominatorer. Men heller, at et hvilket som helst tall med radikaler i denominatorer likte et tall med radikaler på toppen. Dette betydde at tallene med radikaler på toppen var stabile ved divisjon.
Geometri Av Feltutvidelser
feltet du er mest kjent med, er sannsynligvis settet $ \ mathbb Q$ av rasjonale tall. Andre eksempler på felt er settene $ \ mathbb R$ av reelle tall og settet $\mathbb C$ av komplekse tall. Og nå har vi også $ \ mathbb Q{2}$. Siden $\mathbb Q {2}]$ er et felt som inneholder feltet $\mathbb Q$, sier vi at $\mathbb Q{2}] / \mathbb Q$ er en feltutvidelse.faktisk kan det vises at hvis et felt $k$ tilfredsstiller $x+x+ \ldots+x \neq 0$ for all endelig sum og noen $x \neq 0$, må $k $ inneholde $ \ mathbb Q$. Ellers er feltet $k$ nødvendigvis bygget på begrensede felt $\mathbb Z / p\mathbb Z$, også kjent som $\mathbb F_p$, hvor $p$ er prime. I disse feltene er summen av $p$ elementer $x$ alltid lik 0. Faktisk er alle endelige felt $\mathbb F_{p^n} \cong \ mathbb F_p^n $ hvor $n$ er et helt tall og $p$ er prime. Disse begrensede feltene er avgjørende i datavitenskap og kryptografi!det faktum at $ \ mathbb Q{2}] / \ mathbb Q$ er en feltutvidelse gir en veldig naturlig forbindelse mellom de to feltene. Nemlig kan $\mathbb Q{2}$ ses som et vektorrom, hvor $\mathbb Q$ er skalarfeltet. Spesielt det faktum at et hvilket som helst tall i $ \ mathbb Q {2}]$ kan skrives $a \sqrt{2}^2 + b\sqrt{2} + c$ betyr at $(1, \sqrt{2}, \sqrt{2}^2)$ danner grunnlag for $\mathbb Q{2}]$ som et $\mathbb Q$-vektorrom. Og dette betyr at vi kan representere det geometrisk som et 3-dimensjonsrom!
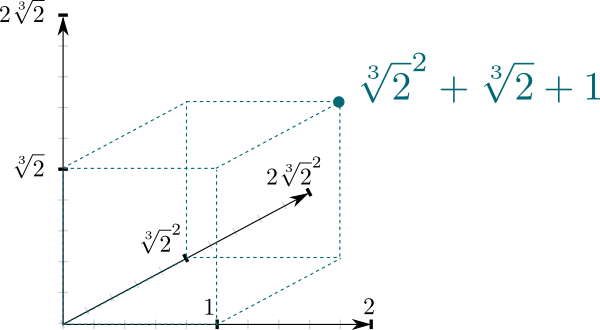
dimensjonen av vektorrommet ovenfor er en interessant egenskap for feltutvidelser. Det er kjent som graden, og det er vanligvis betegnet $ \ big{2}]: \ mathbb Q \ big] = 3$ for eksempel.
Ja! Det er faktisk ganske enkelt å lage en feltutvidelse av dette: bare legg til noe radikalt tall som ikke tilhører $\mathbb Q{2}]$!
Ja! Dette ville skape feltet $(\mathbb Q{2}]) = \mathbb Q{2},\sqrt{2}]$. Dette feltet inneholder alle tall som er produkter og summer på $\sqrt{2}$ og $\sqrt{2}$. Disse er av skjemaet $a\sqrt {2}^2$ + $b \ sqrt{2} + c$ + $ d \ sqrt{2}^2 \ sqrt {2}$ + $ e \ sqrt{2} \sqrt{2} $ + $ f \ sqrt{2}$. Noen ide om hva graden $ \ big{2}, \sqrt{2}]: \mathbb Q{2}]\big]$ er?
Ja! Faktisk har vi $a\sqrt{2}^2$+$b\sqrt{2}$+$c $+$ d\sqrt{2}^2\sqrt{2} $+$ e \sqrt{2} $ + $ f \sqrt{2} $ = $ (a \sqrt{2}^2+b\sqrt{2}+c) $+ $(d\sqrt{2}^2 + e\sqrt{2} + f) \sqrt{2}$. Dermed kan et hvilket som helst antall $\mathbb Q {2},\sqrt {2}]$ skrives $A + b\sqrt{2}$, hvor $a$ og $B$ tilhører $ \ mathbb Q{2}]$. Dermed bestemmer 2 skalarer på $\mathbb Q{2}]$ et tall i $\mathbb Q{2},\sqrt{2}]$. Dette betyr at graden av feltutvidelsen $\mathbb Q{2}, \sqrt{2}] / \mathbb Q{2}]$ er 2. Faktisk har Vi Chasles-forholdet $ \ big{2}, \sqrt{2}]: \mathbb Q \ big] $ = $ \ big{2}, \sqrt{2}] : \mathbb q{2}] \ big] \ big{2}]: \mathbb Q \ big] $ = $ 2 \ ganger 3 = 6$.
det er bedre enn det! Enhver feltutvidelse av endelig grad, kalt endelig feltutvidelse, strekkes av et enkelt tall. For eksempel $\mathbb q{2}, \sqrt{2}] $=$ \mathbb Q{2} + \sqrt{2}]$, som betyr at alle tall som er summer av krefter på $\sqrt{2}$ og $\sqrt{2}$ er også summer av krefter på $\sqrt{2} + \sqrt{2}$. Er det ikke overraskende fantastisk?
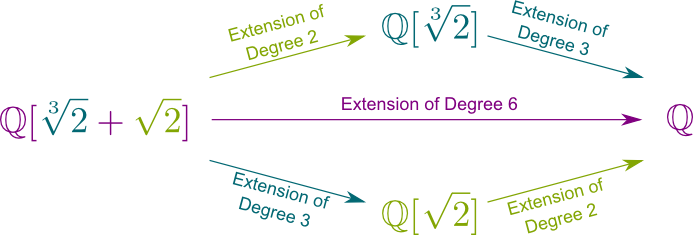
mer generelt kan en endelig feltutvidelse på $ \ mathbb Q$ skrives $ \ mathbb Q $ med noen $ x$ som legges til $ \ mathbb Q$.
Ja. Det er tilfelle for feltutvidelsen $\mathbb R / \mathbb Q$. Og det er også Den viktigste feltutvidelsen I Galois-teorien! Denne feltutvidelsen er $ \ bar {\mathbb Q} / \mathbb Q$, hvor $ \ bar {\mathbb Q}$ er settet med algebraiske tall. Dette er alle løsninger på polynomligninger av skjemaet $a_n x^n $ + $ a_{n-1} x^{n-1} $+$ … $+$ a_1 x $ + $ a_0 = 0$. For eksempel er $\sqrt{2}$ et algebraisk tall fordi det er løsning på $x^4 – 2x = 0$. Dermed er $ \ bar {\mathbb Q}$ en feltutvidelse til alle endelige feltutvidelser på $\mathbb Q$.
Konjugerte Tall
Vi er nesten der! Vi trenger en endelig omvei gjennom polynomligninger.

Nøyaktig! Galois la merke til at noen ligninger kunne forenkles. For eksempel kan $x^4-2x=0$ faktoriseres som $x (x^3-2) = 0$, som tilsvarer $x=0$ eller $x^3-2=0$. Så kan ligningen $x^4-2x=0$ reduseres til ligninger $x=0$ og $x^3-2=0$. Og faktisk er denne reduksjonen veldig lik hvordan tall som 35 kan reduseres til 5 og 7, fordi $5 \ ganger 7 = 35$. Likheten mellom ligninger og hele tall er så sterk at vi selv kan lage Euklidiske divisjoner av polynomer, akkurat som du lærte å gjøre det for tall! Til høyre er et eksempel på en slik divisjon (ikke bekymre deg hvis du ikke forstår det, det vil ikke være viktig for oppfølgeren).
Nøyaktig! Disse er kjent som irreducible polynomligninger. Ligningen $x^3-2=0$ er et eksempel på irreducible polynom ligning.Du har bare faktorisert det som $x^3-2$=$(x-\sqrt{2})$ $(x^2+\sqrt{2}x+\sqrt{2}^2)$!
Ja! Men avgjørende, Galois ønsket å fokusere på ligninger med rasjonelle koeffisienter. Eller heller polynomer med koeffisienter som tilhører basisfeltet. Så, det jeg mente var at for $ \ mathbb Q $ som basisfeltet, er $ x^3-2=0$ irreducible. Rimelig nok… Så hva er så interessant med irreducible polynomligninger?
la oss vurdere $x^2-2x -1=0$ for å få noen ledetråder. Denne ligningen kan bevises å være irreducible. Husker du hvordan du løser det?
hvis $b^2 – 4ac \geq 0$, ja.
Nøyaktig! Så, den irreducible polynomligningen $x^2 + 2x -1=0$ har to løsninger: $1 + \sqrt{2}$ og $1 – \sqrt{2}$ … noen kommentar?
Bingo! Det er nøkkeloppdagelsen Av Galois. Mer Generelt Kalles Galois konjugater alle løsningene til en irreducible polynomligning. Og som du kan forestille deg, er disse avgjørende for å fjerne radikaler fra denominatorer!
Her er en liten vits å huske på den sterke sammenhengen mellom konjugater:

Vurder en brøkdel $1 / x_1$, hvor $x_1$ er et komplisert uttrykk med radikaler. Multiplikasjon opp og ned av konjugatene $x_2$,…, $ x_n $ av $x_1$ gir da $1 / x_1 $ = $ (-1)^n a_n x_2 … x_n/a_0$, som ikke har noen radikal i nevnen som vi har etablert $a_0$ for å være et ikke-nullnummer av basisfeltet!
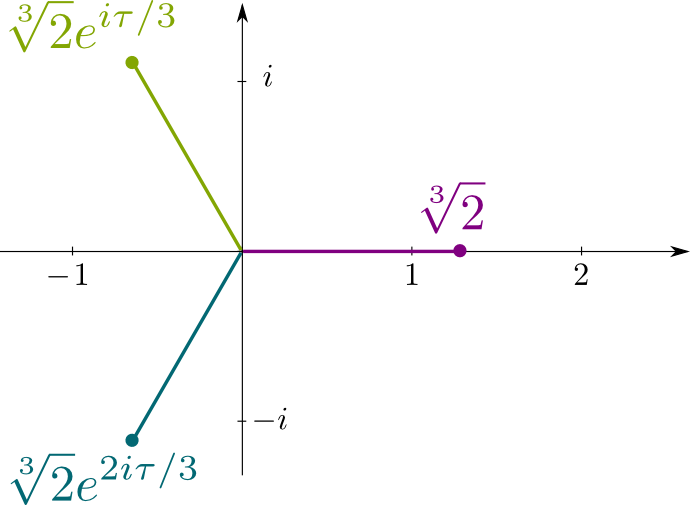
Husk at $x^3-2=0$ er den irreducible polynomligningen $\sqrt{2}$ er løsningen av. Så er dens konjugater de andre løsningene til den ligningen, som er de komplekse tallene $\sqrt{2}j$ og $\sqrt{2}j^2$, hvor $j= e^{i \ tau/3} $ med $\tau = 2 \ pi$ er forholdet mellom omkretsen av en sirkel ved sin radius. Følgende figur viser plasseringen av de konjugerte løsningene i dette komplekse planet:
Galois’ Tvetydighet
Endelig kommer Vi Til Galois nøkkelinnsikt!
Konjugater er helt permutable. Dette betyr at hvis du systematisk endrer $\sqrt{2}$ ved sin konjugat $ – \sqrt{2}$, holder likhetene fortsatt. For eksempel, siden vi hadde $1/(\sqrt{2}-1) = \sqrt{2} + 1$, kan jeg rett og slett fortelle deg at $1/(-\sqrt{2}-1)=-\sqrt{2}+1$! På samme måte har vi følgende fantastiske implikasjon:
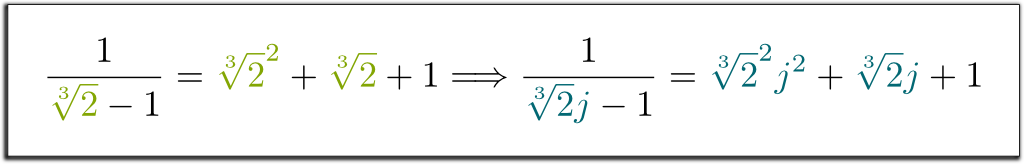
Hehe… La meg først huske at begrensede felt strekkes av et enkelt element. Så, hvis basisfeltet er $\mathbb Q$, kan et endelig felt skrives $\mathbb Q$ for noen rett $ x_1$. Nå, vurder $x^n + a_{n-1}x^{n-1} $ + $ … + a_1 x + a_0 = 0$ den irreducible polynomligningen $x_1$ er løsningen av. Så, hva definerer $ \ mathbb Q$ er $\mathbb Q $ – vektorrommet spannet av $x_1$, $x_1^2$,…, $x_1^{n-1}$, med forenkling av større krefter på $x_1$ i henhold til den algebraiske regelen $x_1^n $ = $ – a_{n-1}x_1^{n-1} $ – $ … – a_0$.Så $ \ mathbb Q $ kan bygges utelukkende på disse algebraiske reglene?
Nøyaktig! Avgjørende er disse algebraiske reglene for $ \ mathbb Q$ egentlig ikke avhengig av arten av $x_1$; de er bare avhengige av det irreducible polynomet $x_1$ er løsningen av! Derfor er reglene for $ \ mathbb Q$ identiske med disse av $\mathbb Q$,…, $\mathbb Q$, hvor $x_1$ erstattes av en av dens konjugater $x_2$,…, $x_n$. Spesielt opererer feltene $\mathbb Q{2}]$ og $\mathbb Q{2} j] $ i henhold til nøyaktig samme regler. Det er derfor konjugater er helt permutable! Vi sier at feltene $\mathbb Q {2}]$ og $\mathbb Q {2} j]$ er isomorfe, og at erstatning $\sqrt{2}$ av $\sqrt{2}j$ er en isomorfisme $\mathbb Q {2}] \rightarrow \ mathbb Q{2}j]$. Mer generelt kalles feltet konstruert på algebraiske regler avledet fra en irreducible polynomligning bruddfeltet til den irreducible polynomligningen. Betegner $P$ polynomet, dette bruddfeltet skrives ofte $ \ mathbb Q / (P)$.Så, $ \ mathbb Q {2}]$ og $ \ mathbb Q{2}j]$ er faktisk mer eller mindre det samme?
på en veldig lik (men sterkere) måte at to vektorrom av dimensjon 2 er mer eller mindre det samme! Dette har en forferdelig konsekvens. Det betyr at det fra et algebraisk perspektiv er meningsløst å gjøre en forskjell mellom et tall og noen av dets konjugater (så lenge du systematisk erstatter tallet med dets konjugat)! Så, for eksempel, $\sqrt {2}$ og $ – \sqrt{2}$ er algebraisk uutslettelig! For å holde dette i bakhodet, her er en annen vits jeg har kommet opp med:

Ikke i det hele tatt! Ethvert skille mellom disse to tallene må innebære annen matematikk enn algebra, som ordrelasjoner eller topologi. Det jeg mener er at for eksempel forholdet $\sqrt{2} > 0$ gjør en forskjell mellom $\sqrt{2}$ av $-\sqrt{2}$, men det er fordi det innebærer en ordreforhold. Men hvis vi begrenser oss til polynomiske likheter, så er det absolutt ingen forskjell mellom $\sqrt{2}$ og $ – \sqrt{2}$. På samme måte er $i$ og $ – i$, løsningene av den irreducible polynomligningen $x^2 + 1=0$, også algebraisk uutslettelig. Likevel kaller vi vilkårlig $i$ en av dem. Derfor Kalte Galois sin teori teorien om tvetydighet. I dag kalles tvetydigheten av valget av den konvensjonelle kvadratroten på $-1 $ blant $i$ og $ – i$ heller symmetrien mellom $i$ og $ – i$.
Galois Grupper
Galois spesielt fokusert på feltutvidelser som er stabile ved konjugering. Slike stabile feltutvidelser er nå kjent Som Galois extensions. Så, hvis $x_1$ tilhører En Galois-utvidelse, inneholder Denne Galois-utvidelsen alle dens konjugater $x_2$,…, $x_n$.
en enkel måte Å konstruere Galois-utvidelser på består i å ta feltet spredt av løsninger av en irreducible polynomligning. For eksempel, hvis $x_1$,…, $x_n$ er konjugater for basisfeltet $\mathbb Q$, så er $\mathbb Q / \mathbb Q$ En Galois-utvidelse. Felt konstruert på denne måten kalles splitting felt.
for eksempel er splittfeltet av ligning $x^3-2=0$ Galois-utvidelsen $\mathbb Q{2}, \sqrt{2} j, \sqrt{2} j^2] / \mathbb Q$ spredt av sine løsninger.
hvis $x_1$ spenner Over En Galois-utvidelse, så gjør det også konjugater. Dermed er $ \ mathbb Q = \mathbb Q = $ … $ = \mathbb Q$ = $ \ mathbb Q$. Dermed er isomorfismen mellom $ \ mathbb Q$ Og $\mathbb Q $ som består i å alltid erstatte $x_1$ med $x_2$, faktisk en isomorfisme mellom $ \ mathbb Q $ og seg selv! Vi kaller det en automorfisme. Automorfismer Av En Galois-utvidelse$\mathbb Q/ \ mathbb Q $ danner Galois-gruppen $Gal (\mathbb Q/\mathbb Q)$.
Sikkert! Du kan legge merke til at $\mathbb Q = \mathbb Q$ og $\mathbb Q = \mathbb Q$, noe som betyr at $i$ og $\sqrt{2}$ hver spenner over splittefeltene i den irreducible polynomligningen de er løsning av. Dermed er $ \ mathbb Q / \ mathbb Q$ og $\mathbb Q / \mathbb Q$ Begge Galois-utvidelser. Derfor består deres automorfismer i å erstatte $i$ med en av dens konjugater, $i $eller$- i$, og erstatte $\sqrt{2} $ med $\sqrt {2} $ eller $ – \sqrt{2}$. I de første tilfellene endrer vi ikke noe til tall, noe som tilsvarer nullsymmetrien. De andre tilfellene kan visualiseres som aksiale symmetrier, som vist i figuren nedenfor:

Er det ikke fantastisk?
Sikkert! La oss komme til splitting feltet $\mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] $ av $ x^3-2=0$. Men før vi går videre, la oss legge merke til at $ \ mathbb Q{2},\sqrt{2}j, \sqrt{2}j^2] = \mathbb Q{2}, j]$.
Alt vi trenger å bevise er at alle generatorer av ett felt tilhører den andre. La oss begynne med å bevise at generatorene til sistnevnte, $\sqrt{2}$ og $j$, tilhører den tidligere. Det er åpenbart for $\sqrt{2}$. Nå, $j = (\sqrt{2} j) / \sqrt{2}$, dermed $j$ tilhører det tidligere feltet også. Dette viser at alle elementene i $\mathbb Q{2},j] $ tilhører $\mathbb Q{2}, \sqrt {2} j, \sqrt{2} j^2]$. Gjensidig er det greit at alle generatorer av det tidligere feltet, $\sqrt{2}$, $\sqrt{2}j$ og $\sqrt{2}j^2$, er produkter av generatorene til sistnevnte. Dermed er begge feltene like. Og spesielt er $\mathbb Q{2}, j] / \mathbb Q$ En Galois-utvidelse.
Hehe … for å forstå symmetrier av $ \ mathbb Q {2}]$, må Vi gå videre I Galois ‘ studie Av Galois-grupper…
Galois Korrespondanse
problemet Med Galois-grupper er at De kan bli ekstremt store og kompliserte. Dette er spesielt tilfelle av den uendelige gruppen $Gal (\bar{\mathbb Q}/\mathbb Q)$. For å pågripe slike store og komplekse grupper, Galois hadde den geniale ideen å bryte disse i mindre biter.
jeg vet! Jeg liker å visualisere disse symmetrier som måter å plugge $ \ mathbb Q{2},j] $ på $ \ mathbb Q$. Her er et avbildet bilde av «plugging on»:
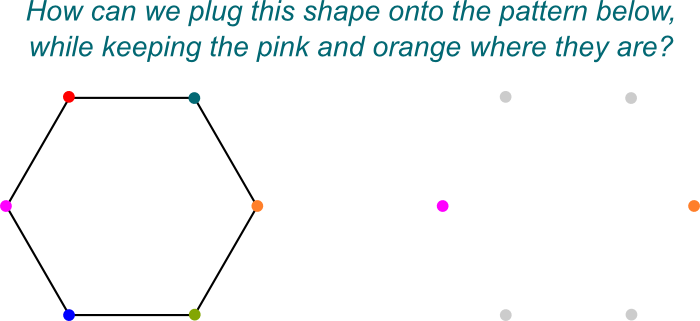
Nøyaktig! Og det er rett og slett fordi $ \ mathbb Q{2},j]$ er En Galois forlengelse av $\mathbb Q $ som selv er en feltutvidelse på $ \ mathbb Q$.
Og det er mer! Galois viste at alle undergrupper Av En Galois extensions er oppnådd på denne måten! Nærmere bestemt er kartleggingen av et hvilket som helst felt $K$ mellom Galois-utvidelsen $\mathbb Q{2},j]$ og basisfeltet $\mathbb Q$ Til Galois-gruppen $Gal (\mathbb Q{2},j] / K)$ bijektiv. Dette faktum kalles Galois korrespondanse! Denne korrespondansen vises skjematisk nedenfor for En Galois-utvidelse $\mathbb Q / \mathbb Q$.

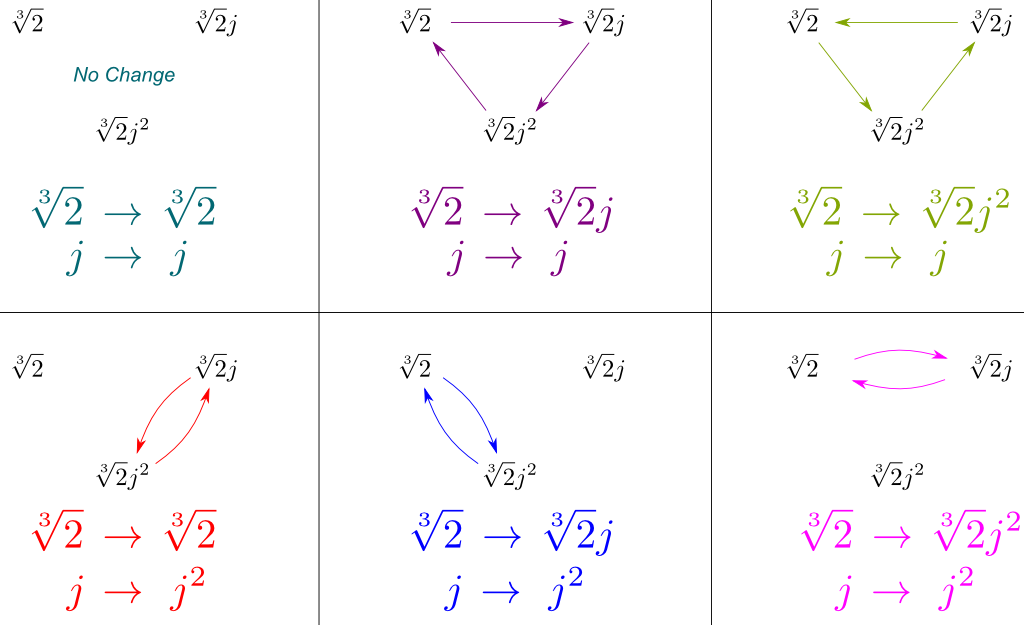
Figuren ovenfor inneholder Alle symmetrier av $Gal (\mathbb Q{2},j]/\mathbb Q)$. Og utrolig, disse symmetrier tilsvarer velkjent gruppe av symmetri.
Jeg lar Marcus du Sautoy presentere den til deg:
Så er symmetrier her som en sjøstjerne eller som en trekant?
ja, faktisk! Denne gruppen av symmetrier av trekanten kalles $D_3$, og den er den samme som gruppen $S_3$ av permutasjoner av 3 elementer. Dette fører oss til følgende formel, som jeg fant så vakker, at jeg har bestemt meg for å ramme den!
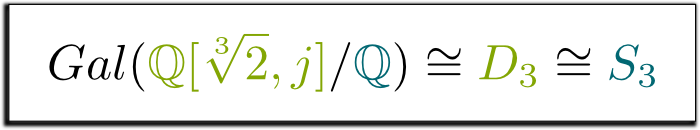
La Oss Konkludere
På Mange måter Er Galois å anse som far til moderne algebra. Hans viktigste innsikt var å se på matematikk gjennom vinkelen av reglene for operasjoner, og dette førte ham til å avsløre overraskende og innsiktsfulle tvetydigheter, eller symmetrier, mellom tall. Fra et algebraisk perspektiv er tall som $\sqrt{2}$, $\sqrt{2}j$ og $\sqrt{2}j^2$ faktisk helt symmetriske og helt utskiftbare.