Grenser i Genetikk
Introduksjon
Effektiv populasjonsstørrelse (Ne) er en viktig genetisk parameter som estimerer mengden genetisk drift i en befolkning, og har blitt beskrevet som størrelsen på en idealisert wright–Fisher-befolkning som forventes å gi samme verdi av en gitt genetisk parameter som i befolkningen under studien (Crow and Kimura, 1970). Ne størrelser kan påvirkes av svingninger i folketellingen populasjonsstørrelse( Nc), av avl kjønn ratio og variansen i reproduktiv suksess.ne estimering kan oppnås ved hjelp av tilnærminger som faller inn i tre metodiske kategorier: demografisk, stamtavlebasert eller markørbasert (Flury et al., 2010). Stamtavle data har tradisjonelt blitt brukt til å skaffe ne estimater i husdyr. Imidlertid er pålitelige estimater av Ne avhengig av at stamtavlen er fullført. Denne tilstanden av kunnskap er mulig i enkelte innenlandske befolkninger, hvor de demografiske parametrene er nøyaktig overvåket for et tilstrekkelig stort antall generasjoner. Men i praksis er anvendelsen av denne tilnærmingen begrenset til noen få tilfeller som involverer svært administrerte raser (Flury et al.( 2010; Uimari Og Tapio, 2011).en løsning for å overvinne begrensningen av en ufullstendig stamtavle er å estimere den siste trenden I Ne ved hjelp av genomiske data. Flere forfattere har anerkjent At Ne kunne estimeres ut fra informasjon om sammenhengen ulikevekt (Ld) (Sved, 1971; Hill, 1981). LD beskriver ikke-tilfeldig forening av alleler i forskjellige loci som en funksjon av rekombinasjonshastigheten mellom de fysiske posisjonene til loci i genomet. LD-signaturer kan imidlertid også skyldes demografiske prosesser som blanding og genetisk drift (Wright, 1943; Wang, 2005), eller gjennom prosesser som «hitchhiking» under selektive feier (Smith Og Haigh, 1974) eller bakgrunnsvalg (Charlesworth et al., 1997). I slike scenarier alleler på forskjellige loci bli assosiert uavhengig av deres nærhet i genomet. Forutsatt at en populasjon er lukket og panmiktisk, er LD-verdien beregnet mellom nøytrale ukoblede loci utelukkende avhengig av genetisk drift (Sved, 1971; Hill, 1981). Denne forekomsten kan brukes til å forutsi Ne på grunn av det kjente forholdet mellom variansen I LD (beregnet ved hjelp av allelfrekvenser) og effektiv populasjonsstørrelse (Hill, 1981).
nylige fremskritt innen genotypingsteknologi (f. eks., VED HJELP AV SNP perle arrays med titusenvis AV DNA-prober) har aktivert innsamling av store mengder genom-wide linkage data ideell for å estimere Ne i husdyr og mennesker blant andre (F.Eks Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2010; Uimari og Tapio, 2011; Kijas et al., 2012). Imidlertid mangler et programvareverktøy som muliggjør estimering Av Ne fra LD, og forskere stoler for tiden på en kombinasjon av verktøy for å manipulere data, utlede LD, og har en tendens til å bruke skreddersydde skript for å utføre de riktige beregningene og estimere Ne.
her beskriver Vi SNeP, et programvareverktøy som gjør det mulig å estimere ne-trender på tvers av generering ved HJELP AV SNP-data som korrigerer for prøvestørrelse, fasing og rekombinasjonshastighet.
Materialer og Metoder
metoden SNeP bruker til å beregne LD avhenger av tilgjengeligheten av fasedata. Når fasen er kjent brukeren kan velge Hill Og Robertson (1968) kvadrert korrelasjonskoeffisient som gjør bruk av haplotype frekvenser for å definere LD mellom hvert par loci (Ligning 1). I fravær av en kjent fase kan imidlertid kvadrert Pearsons produktmomentkorrelasjonskoeffisient mellom par av loci velges. Selv om disse to tilnærmingene ikke er de samme, er de svært sammenlignbare (McEvoy et al., 2011):
hvor pA og pB er henholdsvis frekvensene av alleler A og B på to separate loci (X, y) målt for n individer, pab er frekvensen av haplotypen med alleler a og b i populasjonen som studeres, x og y er de gjennomsnittlige genotypefrekvensene for henholdsvis første og andre locus, xi er genotypen av individuell i ved første locus og yi er Genotypen av individuell i ved andre locus. Ligning (2) korrelerer genotypisk allel teller i stedet for haplotype frekvenser og er ikke påvirket av doble heterozygoter(denne tilnærmingen resulterer i de samme estimatene som –r2 alternativet I PLINK).SNeP estimerer den historiske effektive populasjonsstørrelsen basert på forholdet mellom r2, Ne og c (rekombinasjonsrate), (Ligning 3-Sved, 1971), og gjør det mulig for brukere å inkludere korreksjoner for utvalgsstørrelse og usikkerhet i gametisk fase (Ligning 4—Weir og Hill, 1980):
hvor n er antall individuelle samplet, β = 2 når gametisk fase er kjent og β = 1 hvis i stedet fasen ikke er kjent.
Flere tilnærmelser brukes til å utlede rekombinasjonsraten ved å bruke den fysiske avstanden (δ) mellom to lokaliteter som referanse og oversette den til koblingsavstand (d), som vanligvis beskrives Som Mb(δ) δ For små verdier av d er sistnevnte tilnærming gyldig, men for større verdier av d øker sannsynligheten for flere rekombinasjonshendelser og forstyrrelser, og forholdet mellom kartavstand og rekombinasjonshastighet er ikke lineær, da maksimal rekombinasjonshastighet er 0,5. Således, med mindre du bruker svært kort δ, er tilnærmingen d ≈ c ikke ideell (Corbin et al., 2012). Vi implementerte derfor kartleggingsfunksjoner for å oversette estimert d til c, Etter Haldane (1919), Kosambi (1943), Sved (1971) og Sved og Feldman (1973). I utgangspunktet antyder SNeP d for hvert Par Snp-Er som direkte proporsjonal med δ i henhold til d = kδ hvor k er en brukerdefinert rekombinasjonsverdi (standardverdi er 10-8 som I Mb = cM). Den utledede verdien av δ kan da bli utsatt for en av de tilgjengelige kartleggingsfunksjonene hvis brukeren krever det.
Løse Ligning (3)For Ne og inkludert alle korreksjonene som er beskrevet, tillater prediksjon Av Ne fra LD-data ved hjelp av (Corbin et al., 2012):
Hvor Nt er den effektive befolkningsstørrelsen t generasjoner siden beregnet som t = (2f(ct))-1 (Hayes et al., 2003), ct er rekombinasjonshastigheten definert for en bestemt fysisk avstand mellom markører og eventuelt justert med kartleggingsfunksjonene nevnt ovenfor, r2adj er LD-verdien justert for utvalgsstørrelse og α:= {1, 2, 2.2} er en korreksjon for forekomsten av mutasjoner (Ohta og Kimura, 1971). DERFOR, LD over større rekombinante avstander er informativ på siste Ne mens kortere avstander gi informasjon om fjernere tider i det siste. Et binning-system er implementert for å oppnå gjennomsnittlige r2-verdier som reflekterer LD for bestemte inter-locus-avstander. Binning-systemet implementert bruker følgende formel til å definere minimums – og maksimumsverdiene for hver bin:bimax=minD+(maxD−minD) (bi−1totbins)x (6a)
Eksempelapplikasjon
Vi testet SNeP med to publiserte datasett som tidligere hadde blitt brukt til å beskrive trender I Ne over tid ved HJELP AV LD, Bos indicus og Ovis aries . R2-estimatene for storfe datasettene ble oppnådd av forfatterne ved Hjelp Av GenABLE (Aulchenko et al., 2007) bruk av minimum allelfrekvens (MAF) < 0,01 og justering av rekombinasjonshastigheten ved Hjelp Av Haldanes kartleggingsfunksjon (Haldane, 1919). R2-estimatene av sauedataene ble beregnet av forfatterne ved HJELP AV PLINK-1.07 (Purcell et al., 2007), MED EN MAF < 0,05 og ingen ytterligere rettelser. For begge autosomale datasett er r2-estimater korrigert for utvalgsstørrelse ved hjelp av ligning (4) med β = 2. For disse komparative analysene Inkluderte SNeP-kommandolinjen de samme parametrene som ble brukt for de publiserte dataene, bortsett fra r2-estimatene, beregnet gjennom genotypetall og bruk Av Sneps nye binning-strategi.
Resultater
SNeP Er en multithreaded applikasjon utviklet I C++ og binærfiler for de vanligste operativsystemene (Windows, OSX og Linux) kan lastes ned fra https://sourceforge.net/projects/snepnetrends/. Binærfilene ledsages av en håndbok som beskriver trinnvis bruk Av SNeP for å utlede trender I Ne som beskrevet her. SNeP produserer en utdatafil med tabulatordelte kolonner som viser følgende for hver bin som ble brukt til å estimere Ne: antall generasjoner tidligere som bin tilsvarer (f. eks., 50 generasjoner siden), det tilsvarende ne estimatet, gjennomsnittlig avstand mellom Hvert Par Snper i hyllen, gjennomsnittlig r2 og standardavviket til r2 i hyllen, og antall Snper som brukes til å beregne r2 i hyllen. Denne filen kan enkelt importeres I Microsoft Excel, R Eller annen programvare for å plotte resultatene. Tomtene som vises her (Figur 1, 3) tilsvarer kolonnene for generasjoner siden og Ne fra utdatafilen. Kolonnen med r2-standardavviket er gitt for brukere å inspisere variansen I Ne-estimatet i hver hylle, spesielt for de hyllene som reflekterer eldre tidsestimater og som er mindre pålitelige da antall Snper som brukes til å estimere r2, blir mindre.
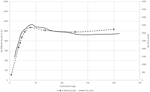
Figur 1. Sammenligning Av ne trender av seks Sveitsiske sauer raser Ifølge Burren et al. (2014) (stiplede linjer) og dette arbeidet (faste linjer).
formatet som kreves for inngangsfilene er standard plink-format (ped-og kartfiler) (Purcell et al., 2007). SNeP lar brukerne enten beregne LD på dataene som beskrevet ovenfor, eller bruke en tilpasset forhåndsberegnet ld-matrise for å estimere Ne ved Hjelp Av Ligning (5).
programvaregrensesnittet lar brukeren kontrollere alle parametere i analysen, f. eks. avstandsområdet mellom SNPs i bp og settet med kromosomer som brukes i analysen (f. eks. 20-23). I Tillegg Inkluderer SNeP muligheten til å velge EN maf terskel (standard 0.05), da det er vist at regnskap FOR MAF resulterer i objektive r2-estimater uavhengig av utvalgsstørrelse (Sved et al ., 2008). Sneps flertrådede arkitektur gir rask beregning av store datasett (vi testet opp til ~100k SNPs for et enkelt kromosom), for eksempel BLE BOS-dataene beskrevet her analysert med en prosessor i 2 ’43», bruken av to prosessorer reduserte tiden til 1 ’43», fire prosessorer reduserte analysetiden til 1 ’05».
Zebu Eksempel
for zebu-analysen viste formene Til ne-kurvene oppnådd Med SNeP og deres publiserte datatrender den samme banen med en jevn nedgang til rundt 150 generasjoner siden, etterfulgt av en utvidelse med en topp rundt 40 generasjoner siden og endte i en bratt nedgang på de siste generasjonene (Figur 1). Men mens trendene i begge kurver var de samme, resulterte de to tilnærmingene i forskjellige ne-estimater, Med Sneps verdier omtrent tre ganger større enn de i originalpapiret. Mens vi forsøkte å bruke forfatterens parametere i våre analyser, var noen forskjeller uunngåelige, det vil si den opprinnelige publikasjonen av storfe data estimert r2 med en annen tilnærming til den implementert I SNeP. Analyser med SNeP var basert på genotyper, mens den opprinnelige analysen var basert på utledet to locus haplotyper, noe som resulterer i publiserte data som viser en forventet r2 på 0,32 på minimumsavstanden, mens våre estimater var 0,23. Tilsvarende Mbole-Kariuki et al. (2014) fikk et bakgrunnsnivå r2 = 0,013 rundt 2 Mb, mens vårt estimat på samme avstand var 0.0035 (data ikke vist). Følgelig, som våre estimater AV LD var konsekvent mindre Enn Mbole-Kariuki et al. (2014) det forventes at våre ne-estimater skal være større. Mens denne observasjonen fremhever viktigheten av et forsiktig valg av parametrene og deres terskler, er det viktig å markere at selv om den absolutte størrelsen På ne-verdiene er forskjellig, er trendene nesten identiske.
Swiss Sheep Eksempel
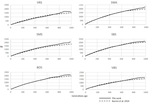
de seks Sveitsiske saueraser analysert Med SNeP produsert sammenlignbare resultater med de fra den opprinnelige papir (Figur 2), med det meste overlappende ne trend kurver (Figur 3). Den generelle trenden i Ne viste imidlertid en nedgang mot nåtiden. SNeP produserte litt større verdier Av Ne for den fjernere fortiden (700-800 generasjoner). Dette skyldes det forskjellige binningssystemet som brukes I SNeP, som gjør det mulig for brukeren å oppnå en jevnere fordeling av parvise sammenligninger i hver bin (dvs ., ANTALL SNP parvis sammenligninger innenfor hver bin er sammenlignbare). For tidsrommet som strekker seg utover 400 generasjoner siden, Burren et al. (2014) brukte bare tre hyller i analysen (sentrert på 400, 667 og 2000 generasjoner siden) mens SNeP i Samme tidsperiode brukte 5 skuffer med en rekke parvise sammenligninger avhengig av rekkevidden definert med formler 6a, b. Følgelig slutter Burren og kollegers tilnærming med en høyere tetthet av data som beskriver de siste generasjonene enn å beskrive de eldste generasjonene. Derfor har bruken av færre hyller en tendens til å øke tilstedeværelsen av mindre verdier Av Ne i hver beholder, og dermed senke gjennomsnittlig ne-verdi for hver beholder. Ne-verdiene for den siste tiden, sammenlignet med den 29. generasjonen tidligere, ga svært like resultater. Den største forskjellen (50) ble oppnådd FOR sbs-rasen.

Figur 2. Sammenligning mellom nyere ne verdier beregnet på 29. generasjon i dette arbeidet Og Burren et al. (2014) for seks Sveitsiske sauer raser.
Figur 3. Sammenligning Av ne trender for de siste 250 generasjonene I SHZ-dataene oppnådd Av Mbole-Kariuki et al. (2014) (stiplede linjer) Og Bruk Av SNeP (heltrukket linje).
Diskusjon
Analyse Av Ne ved HJELP AV LD-data ble først demonstrert for 40 år siden, og har blitt brukt, utviklet og forbedret siden (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). Det tradisjonelt lite antallet Snp-er som analyseres, er ikke lenger en begrensning, SIDEN SNP-Sjetonger består av et ekstremt stort antall Snp-Er, tilgjengelig på kort tid og til en rimelig pris. Dette har økt bruken av metoden, som har blitt brukt på mennesker (Tenesa et al., 2007; McEvoy et al., 2011) så vel som til flere domestiserte arter (England et al., 2006; Uimari og Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Sammen med disse forbedringene, metodiske begrensninger har blitt klart og har blitt adressert her, med de fleste av innsatsen peker til riktig estimering av nyere Ne. Likevel er den kvantitative verdien av estimatet svært avhengig av utvalgsstørrelse, TYPE ld estimering og binning prosessen (Waples And Do, 2008; Corbin et al., 2012), mens det kvalitative mønsteret avhenger mer av den genetiske informasjonen enn på datamanipulering.Så langt har denne metoden blitt brukt ved hjelp av en rekke programvare, ingen standardisert tilnærming eksisterer for å bin resultatene, og hver studie har brukt en mer eller mindre vilkårlig tilnærming, for eksempel binning for generasjonsklasser tidligere (Corbin et al., 2012), binning for avstandsklasser med konstant rekkevidde for hver bin (Kijas et al., 2012) eller binning per avstandsklasser på lineær måte, men med større hyller for de nyere tidspunktene (Burren et al., 2014). Så vidt vi vet Den eneste programvaren tilgjengelig som anslår Ne GJENNOM LD Er NeEstimator (Do et al., 2014), en oppgradert versjon av den tidligere LDNE (Waples and Do, 2008) som tillater analyse av store datasett (som 50k SNPChip). Det er viktig at Mens SNeP fokuserer på å estimere historiske ne-trender, Er Neestimators mål å produsere moderne objektive ne-estimater, sistnevnte bør derfor betraktes som et komplementært verktøy mens man undersøker demografi gjennom LD.
Vi brukte SNeP til å analysere to datasett der metoden tidligere ble brukt. Resultatene vi fikk for sau data var både kvantitativt og kvalitativt sammenlignbare med de som oppnås Ved Burren et al. (2014), mens For Zebu-dataene fikk vi et ne-trendestimat som tett matchet Mbole-Kariuki et al. (2014) selv om våre poengestimater Av Ne var større enn de som er beskrevet for dataene (Mbole-Kariuki et al., 2014). Uoverensstemmelsen mellom disse to resultatene gjenspeiler At Burren og kolleger produserte sine r2-estimater ved HJELP AV PLINK (standardprogramvaren for STORSKALA SNP-datamanipulering) som bruker samme tilnærming som brukes til å estimere r2 Av SNeP, Mens Mbole-Kariuki et al. fulgte Hao et al. (2007) for vurdering av r2. Bruken av forskjellige estimater for LD er kritisk for det kvantitative aspektet Av ne-kurven, der på grunn av den hyperbolske korrelasjonen Mellom Ne og r2, kan en reduksjon i r2 på dens rekkevidde nærmere 0 føre til en meget stor endring I ne-estimater, mens forskjeller i estimater er mindre signifikante når r2-verdien er høy, dvs.nærmere 1. Derfor, selv om I et av datasettene ne-verdiene var vesentlig forskjellige, overlappet Ne-kurvene i begge tilfeller Med de som opprinnelig ble publisert.
som allerede foreslått av andre forfattere, må påliteligheten av de kvantitative estimatene som er oppnådd med denne metoden, tas med forsiktighet, spesielt For ne-verdier relatert til de nyeste og eldste generasjonene (Corbin et al., 2012) fordi for nyere generasjoner er store verdier av c involvert, ikke passer de teoretiske implikasjonene Som Hayes foreslo å estimere en variabel Ne over tid (Hayes et al., 2003). Estimater for de eldste generasjonene kan også være upålitelige da koalescerende teori viser at INGEN SNP kan pålidelig samples etter 4ne generasjoner tidligere (Corbin et al., 2012). Videre er ne-estimater, og spesielt de som er relatert til generasjoner videre i fortiden, sterkt påvirket av datamanipulasjonsfaktorer, som valg AV MAF-og alfa-verdier. I tillegg kan binning-strategien som brukes, forstyrre den generelle presisjonen til metoden, for eksempel hvor et utilstrekkelig antall parvise sammenligninger brukes til å fylle hver bin.
en av anvendelsene av metoden er å sammenligne rase demografier. I dette tilfellet vil formen På ne-kurvene være det optimale verktøyet for å skille mellom forskjellige demografiske historier, mer enn deres numeriske verdier, ved å bruke dem som et potensielt demografisk fingeravtrykk for den rasen eller arten, men tatt i betraktning at mutasjon, migrasjon og utvalg kan påvirke ne-estimeringen gjennom LD (Waples and Do, 2010). I tillegg er nøye vurdering av dataene analysert Med SNeP (og annen programvare for å estimere Ne) svært viktig, da tilstedeværelsen av forstyrrende faktorer som blanding kan føre til partiske estimater Av Ne (Orozco-terWengel and Bruford, 2014).Målet Med SNeP er derfor å gi et raskt og pålitelig verktøy for å anvende LD-metoder for å estimere Ne ved hjelp av genotypiske data med høy gjennomstrømning på en mer konsistent måte. Det tillater to forskjellige r2 estimering tilnærminger pluss muligheten til å bruke r2 estimater fra ekstern programvare. Bruken av SNeP ikke overvinne grensene for metoden og teorien bak det, men det tillater brukeren å bruke teorien ved hjelp av alle korreksjoner foreslått til dags dato.
Forfatterbidrag
MB unnfanget og skrev programvaren og manuskriptet. MB, MT og POtW testet programvaren og utførte analysene. MT, POtW og MWB reviderte manuskriptet. Alle forfattere godkjente det endelige manuskriptet.
Interessekonflikt
forfatterne erklærer at forskningen ble utført i fravær av kommersielle eller økonomiske forhold som kan tolkes som en potensiell interessekonflikt.
Takk
Vi takker Christine Flury for å gi sauene data og for nyttig diskusjon. Vi takker også de to anmeldere for nyttige forslag til å forbedre dette papiret. MB ble støttet av programmet Master And Back (Regione Sardegna).Charlesworth, B., Nordborg, M. Og Charlesworth, D. (1997). Effektene av lokalt utvalg, balansert polymorfisme og bakgrunnsvalg på likevektsmønstre av genetisk mangfold i inndelte populasjoner. Genet. Res. 70, 155-174. doi: 10.1017 / S0016672397002954
PubMed Abstract | Full Text / CrossRef Full Text / Google Scholar
Crow, Jf, Og Kimura, M. (1970). En Introduksjon Til Populasjonsgenetikkteori. New York: Harper og Row.
Google Scholar
Ohta, T., Og Kimura, M. (1971). Linkage ulikevekt mellom to segregerende nukleotidsteder under jevn flux av mutasjoner i en endelig populasjon. Genetikk 68, 571-580.
PubMed Abstract | Full Text/Google Scholar
Wright, S. (1943). Isolasjon på avstand. Genetikk 28, 114-138.
PubMed Abstract | Full Text / Google Scholar