Refraksjon, eller bøyning av lys, oppstår når lyset passerer fra ett medium til et annet medium med en annen brytningsindeks. Refraksjon er en viktig egenskap ved linser, slik at de kan fokusere en stråle av lys på et enkelt punkt, og er også ansvarlig for en rekke kjente fenomener, for eksempel den tilsynelatende forvrengningen av objekter som er delvis nedsenket i vann.Brytningsindeks Er definert som den relative hastigheten som lyset beveger seg gjennom et materiale med hensyn til hastigheten i et vakuum. Ved konvensjon er brytningsindeksen til et vakuum definert som å ha en verdi på 1,0. Indeksen for brytning, n, av andre gjennomsiktige materialer er definert gjennom ligningen:

hvor c er lysets hastighet, og v er lysets hastighet i det materialet. Siden brytningsindeksen til et vakuum er definert som 1.0 og et vakuum er blottet for noe materiale, brytningsindeksene for alle gjennomsiktige materialer er derfor større enn 1,0. For de fleste praktiske formål kan brytningsindeksen for lys gjennom luft (1.0003) brukes til å beregne brytningsindekser av ukjente materialer. Brytningsindekser for noen vanlige materialer er presentert i Tabell 1 nedenfor.

Refraktiv indeks luft 1.0003 Water 1.33 Glycerin 1.47 Immersion Oil 1.515 Glass 1.52 Flint 1.66 Zircon 1.92 Diamond 2.42 Lead Sulfide 3.91

Table 1

It is important to note that the speed at which refracted light travels is dependent upon the density of the materials it is traveling through. For eksempel, når lys passerer fra et mindre tett medium, for eksempel luft, til et mer tett medium, for eksempel vann, reduseres hastigheten som den elektromagnetiske bølgen beveger seg på. Alternativt, når lyset passerer fra et mer tett medium til et mindre tett medium, øker bølgens hastighet.

vinkelen som brytes lys reiser, er imidlertid avhengig av både innfallsvinkelen og sammensetningen av materialet som det går inn i. Normal kan defineres som en linje vinkelrett på grensen mellom to stoffer. Lyset passerer inn i grensen i en vinkel mot det normale og brytes i henhold Til Snells Lov:

hvor n representerer brytningsindeksene for materiale 1 og materiale 2 og q symboliserer lysets vinkler som reiser gjennom disse materialene med hensyn til det normale. Det er flere viktige punkter som kan trekkes fra denne ligningen. Når n (1) er større enn n (2), er brytningsvinkelen alltid mindre enn innfallsvinkelen. Alternativt, når n(2) er større enn n (1), er brytningsvinkelen alltid større enn innfallsvinkelen. Når de to brytningsindeksene er like (n (1) = n(2)), blir lyset passert uten brytning.

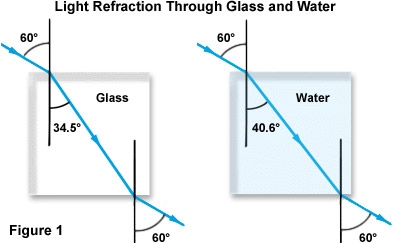
begrepet brytningsindeks er illustrert I Figur 1 nedenfor, med fokus på tilfelle av lys som passerer fra luft gjennom både glass og vann. Legg merke til at mens begge strålene går inn i det tettere materialet gjennom samme innfallsvinkel med hensyn til normal (60 grader), er brytningen for glass nesten 6 grader større enn for vann på grunn av glassets høyere brytningsindeks.

Forskere har funnet ut at brytningsindeksen varierer med frekvensen av stråling (eller bølgelengde) av lys. Dette fenomenet oppstår i forbindelse med alle gjennomsiktige medier og har blitt kalt dispersjon. Derfor, når du måler brytningsindeksen til et gjennomsiktig stoff, må den spesielle bølgelengden som brukes i målingen identifiseres. Nedenfor beskriver Tabell 2 dispersjonen av tre uavhengige bølgelengder i forskjellige medier.

Materiale blå (486,1 nm) gul (589,3 nm) rød (656,3 nm) 1,524 1,517 1,515 flintglass 1.639 1.627 1.622 Water 1.337 1.333 1.331 Cargille Oil 1.530 1.520 1.516 Carbon Disulfide 1.652 1.628 1.618

Table 2

The most commonly used wavelength to measure refractive index is that emitted by a sodium lamp, which has an average wavelength of 5.893 nanometers. Dette lyset kalles D-linjespektret, og representerer det gule lyset som er oppført i Tabell 2 ovenfor. På Samme måte svarer F-og c-linjespektrene til blått og rødt lys av bestemte bølgelengder utgitt av hydrogen. Disse spektrene er grunnleggende i beregningen av dispersjon, som kvantitativt kan defineres som:

hvor n er brytningsindeksen til materialet ved en bestemt bølgelengde betegnet Av D, F Og C, som representerer spektrallinjene av natrium og hydrogen som beskrevet ovenfor. Forholdet er slik at når lysets bølgelengde øker, reduseres brytningsindeksen. Imidlertid spiller mange faktorer en rolle i dispersjonen av ulike materialer, inkludert deres elementære og molekylære sammensetning. Flere uorganiske faste stoffer, som kromater, dikromater, cyanider, vanadater og halogenidkomplekser, har uvanlig høye dispersjoner. Likevel kan organiske substituenter også bidra til høy dispersjon.

	Interactive Java Tutorial
Lysbrytning Oppdag hvordan bølgelengden og hendelsesvinkelen til lyset påvirker brytningen i en rekke medier med forskjellige brytningsindekser.

Refraction of light is particularly important in the construction and physics of lenses. Husk at når lysstrålen forlot både glasset og vannet I Figur 1, ble det igjen brutt i samme vinkel som det kom inn i materialet. Dette konseptet er viktig for linsens funksjon, selv om formen på objektivet påvirker det resulterende bildet betydelig. I en konveks linse, som vist nedenfor I Figur 2, er lysbølger reflektert fra objektet, i dette tilfellet en giraffe, bøyd mot det optiske sentrum av linsen og konvergerer på fokuspunktet.

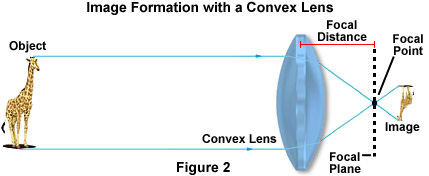
objektets relative posisjon med hensyn til objektivets fremre fokuspunkt bestemmer hvordan objektet avbildes. Hvis objektet er over to ganger lengden på brennpunktet, vises det mindre og invertert og må avbildes av en ekstra linse for å forstørre størrelsen. Men når bildet er nærmere linsen enn fokuspunktet, vises bildet oppreist og større, som lett kan demonstreres med et enkelt forstørrelsesglass.

	Interactive Java Tutorial
Bildeforstørrelse Utforsk hvordan bildet av en giraff forstørres av brytning av lysbølger som passerer gjennom en enkel tynn bi-konveks linse.

Due to the refraction of light, a common optical illusion occurs when objects are visualized in water. En enkel sugerør i et glass fylt med vann, som illustrert i Figur 3, er et godt eksempel på denne forekomsten. I dette eksemplet må lysbølger først passere gjennom vannet, deretter gjennom glass / vanngrensen, og til slutt gjennom luften. Lysbølgene som reflekteres fra halmens ender brytes i større grad enn de som kommer fra halmens midtpunkt, slik at halmen virker forstørret og litt forvrengt.

det samme fenomenet kan brukes til å bestemme brytningsindeksen til en væske med et optisk mikroskop. For å gjøre dette må en flat celle som er i stand til å holde væske med et merke (eller graderinger) plasseres på innsiden av glassoverflaten. Også, en av mikroskop okularene må ha en gradert retikkel satt inn på det primære bildeplanet for linjebreddemålinger av merket i den flate cellen. Før du legger væsken med ukjent brytningsindeks til cellen, bør mikroskopet være fokusert på merket nederst i cellen og en måling av merkets posisjon på retikkelen som er notert. Deretter skal en liten mengde væske legges til cellen og mikroskopet refokuseres på merket (gjennom væsken) og en ny måling tatt. Mikroskopet skal da endelig fokuseres på overflaten av væsken, og en tredje lesing registreres ved å måle posisjonen til merket på retikkelen. Brytningsindeksen til den ukjente væsken kan deretter beregnes ved hjelp av følgende ligning:

Hvor D(målt) er målt dybde (fra overflaten av væsken til posisjonen til merket på den tomme cellen) ved hjelp av mikroskopet og D(tilsynelatende) er merket måling med og uten væske.

den kritiske refleksjonsvinkelen er et annet nøkkelbegrep i studiet av lysbrytning og er illustrert nedenfor i Figur 4. Når lys passerer gjennom et medium med høy brytningsindeks til et medium med lavere brytningsindeks, blir hendelsesvinkelen til lysbølgene en viktig faktor. Hvis hendelsesvinkelen øker forbi en bestemt verdi (avhengig av brytningsindeksen til de to mediene), vil den nå et punkt der vinkelen er så stor at ingen lys brytes inn i mediet med lavere brytningsindeks.

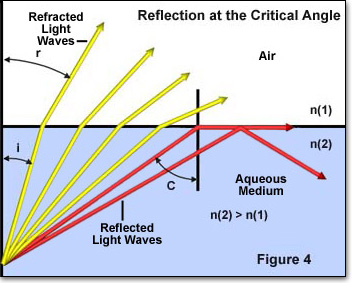
I Figur 4 representeres individuelle lysstråler av enten røde eller gule fargede piler som beveger seg fra et medium med høy brytningsindeks (n (2)) til en med lavere brytningsindeks(n (1)). Innfallsvinkelen for hver enkelt lysstråle er betegnet med i og brytningsvinkelen ved r. de fire gule lysstrålene har alle en innfallsvinkel (i) lav nok til å passere gjennom grensesnittet mellom de to mediene. Imidlertid har de to røde lysstrålene hendelsesvinkler som overskrider den kritiske vinkelen (ca. 41 grader) og reflekteres enten inn i grensen mellom mediet eller tilbake til det høye brytningsindeksmediet. Dette fenomenet skjer når brytningsvinkelen (vinkel r I Figur 4) blir lik 90 grader og Snells lov reduseres til:

hvor (q) nå kalles den kritiske vinkelen C. hvis mediet med mindre brytningsindeks er luft (n = 1.00), reduserer ligningen ytterligere til:

som diskutert tidligere er et annet viktig trekk ved lysbrytning at lysets bølgelengde påvirker mengden brytning som oppstår i et medium. Faktisk er mengden brytning som finner sted omvendt proporsjonal med bølgelengden til det innfallende lyset. Dermed brytes kortere bølgelengde synlig lys i større vinkel enn lengre bølgelengde lys. Følgelig, når hvitt lys, som består av alle fargene i det synlige spektret, føres gjennom et glass prisme, det er spredt i sin komponent farger på en måte som er avhengig av de enkelte bølgelengder. Lavfrekvent synlig lys (600 nanometer og større) brytes i mindre vinkel enn høyere frekvenslys, noe som resulterer i en regnbuelignende effekt, som illustrert nedenfor i Figur 5.

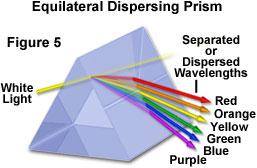
dette samme fenomenet er også ansvarlig for kromatisk aberrasjon. Når hvitt lys sendes gjennom en enkel konveks linse, oppstår flere fokuspunkter i nærheten som tilsvarer de mindre brytningsindeksforskjellene i komponentbølgelengdene. Denne effekten har en tendens til å produsere farget (enten rød eller blå, avhengig av fokus) haloer rundt bildene av objekter. Korrigering av dette avviket oppnås vanligvis ved bruk av kombinasjoner av to eller flere linseelementer sammensatt av materialer som har forskjellige dispersive egenskaper, for eksempel en akromatisk linse konstruert med både krone-og flintglass.

	Interactive Java Tutorial
Refraksjon av Et Prisme Undersøk hvordan hvitt lys separeres i komponentfargene ved brytning gjennom ulike vinkler i et prisme.

Over the years, humans have made many devices that make use of the fact that light can be refracted, as well as reflected and focused. Det vanligste eksempelet er et kamera, som er designet for å skape skarpe og fokuserte bilder på en emulsjon av film eller overflaten av en ladekoblet enhet (CCD) for å produsere et nøyaktig bilde. Andre optiske enheter som utnytter disse egenskapene til lys inkluderer mikroskoper og teleskoper, som gjør det mulig å se på objekter som er usynlige for det blotte menneskelige øye, uansett om de befinner seg på hodet på en pinne eller i en fjern galakse.

Bidragsytere

Mortimer Abramowitz – Olympus America, Inc., To Corporate Center Drive. Melville, New York, 11747.Shannon H. Neaves Og Michael W. Davidson-Nasjonalt Høyt Magnetfeltlaboratorium, 1800 East Paul Dirac Dr., Florida State University, Tallahassee, Florida, 32310.

TILBAKE TIL LYS og FARGE

Spørsmål eller kommentarer? Send oss en e-post.

© 1998-2021 Av Michael W. Davidson og Florida State University. Alle Rettigheter Reservert. Ingen bilder, grafikk, skript eller applets kan reproduseres eller brukes på noen måte uten tillatelse fra rettighetshaverne. Bruk av dette nettstedet betyr at du godtar Alle De Juridiske Vilkårene som er angitt av eierne.

dette nettstedet vedlikeholdes av Vår
Grafikk & Web Programmering Team
i samarbeid Med Optisk Mikroskopi på
National High Magnetic Field Laboratory.

Siste endring: fredag, November 13, 2015 på 02: 18 PM

Tilgang Teller Siden Mars 10, 2003:181405

Besøk nettstedene til våre partnere i utdanning: