Kalman filters

algoritmen som brukes til å slå sammen dataene kalles Et Kalmanfilter.

Kalman-filteret er en Av de mest populære algoritmer i datafusjon. Oppfunnet I 1960 Av Rudolph Kalman, er det nå brukt i våre telefoner eller satellitter for navigasjon og sporing. Den mest kjente bruken av filteret var Under Apollo 11-oppdraget for å sende og bringe mannskapet tilbake til månen.

når skal Du bruke Et Kalman-Filter ?

Et Kalmanfilter kan brukes til datafusjon for å estimere tilstanden til et dynamisk system (utvikler seg med tiden) i nåtiden (filtrering), fortiden (utjevning) eller fremtiden (prediksjon). Sensorer innebygd i autonome kjøretøy avgir tiltak som noen ganger er ufullstendige og støyende. Sensorens unøyaktighet (støy) er et svært viktig problem og kan håndteres Av Kalman-filtre.

Et Kalmanfilter brukes til å estimere tilstanden til et system, betegnet x. denne vektoren består av en posisjon p og en hastighet v.

ved hvert estimat knytter vi et mål for usikkerhet p.

ved å utføre en fusjon av sensorer tar vi hensyn til forskjellige data for samme objekt. En radar kan anslå at en fotgjenger er 10 meter unna, Mens Lidar anslår det til å være 12 meter. Bruken Av Kalman-filtre lar deg få en presis ide å bestemme hvor mange meter egentlig er fotgjengeren ved å eliminere støyen fra de to sensorene.

Et Kalmanfilter kan generere estimater av tilstanden til objekter rundt det. For å gjøre et estimat trenger det bare de nåværende observasjonene og forrige prediksjon. Målehistorikken er ikke nødvendig. Dette verktøyet er derfor lett og forbedrer seg med tiden.

Hvordan det ser ut

Tilstand og usikkerhet er representert Av Gaussere.

figcaption>

en gaussisk er en kontinuerlig funksjon der området er 1. Dette gir oss mulighet til å representere sannsynligheter. Vi er på en sannsynlighet for normalfordeling. Uni-modaliteten Til Kalman-filtrene betyr at vi har en enkelt topp hver gang for å estimere tilstanden til systemet.

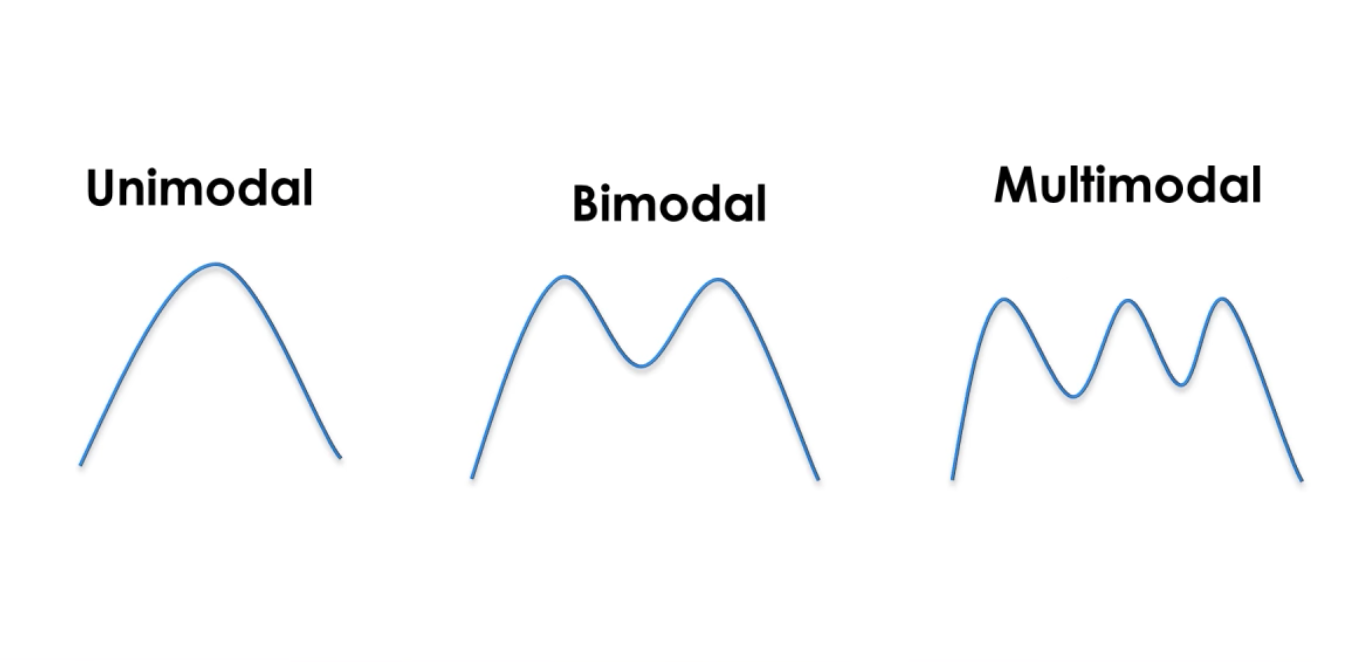unimodal vs multimodal (kilde)

vi har en middelverdi som representerer en tilstand og en varians σ2 som representerer en usikkerhet. Jo større variansen er, desto større er usikkerheten.

Gaussians make it possible to estimate probabilities around the state and the uncertainty of a system. A Kalman filter is a continuous and uni-modal function.

Bayesian Filtering

In general, a Kalman filter is an implementation of a Bayesian filter, ie a sequence of alternations between prediction and update or correction.

Prediction: We use the estimated state to predict the current state and uncertainty.
Update: Vi bruker observasjonene til våre sensorer for å korrigere den forutsagte tilstanden og få et mer nøyaktig estimat.

For å gjøre et estimat trenger Et Kalmanfilter bare nåværende observasjoner og forrige prediksjon. Målehistorikken er ikke nødvendig.

Matematikk

matematikken bak Kalmanfiltrene er laget av tillegg og multiplikasjoner av matriser. Vi har to faser: Prediksjon og Oppdatering.

Prediksjon
vår prediksjon består av å estimere en tilstand x ‘og en usikkerhet P’ på tid t fra de tidligere tilstandene x og P på tid t-1.

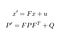
Prediksjonsformler

• f: overgangsmatrise fra t-1 til t
• ν: støy lagt
• q: Oppdateringsfasen består av å bruke en z-måling fra en sensor for å korrigere vår prediksjon og dermed forutsi x og P.
  

  

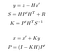
  oppdater formler

  • y: forskjell mellom faktisk måling og prediksjon, dvs.feilen.
  • S: Estimert systemfeil
  • H: Matrise av overgang mellom markøren til sensoren og vår.
  • R: Kovariansmatrise relatert til sensorstøy(gitt av sensorprodusenten).
  • K: Kalman gevinst. Koeffisient mellom 0 og 1 reflekterer behovet for å korrigere vår prediksjon.

  oppdateringsfasen gjør det mulig å estimere en x og En P nærmere virkeligheten enn hva målingene gir.

  Et Kalman-filter tillater spådommer i sanntid, uten data på forhånd. Vi bruker en matematisk modell basert på multiplikasjon av matriser for hver gang vi definerer en tilstand x (posisjon, hastighet) Og usikkerhet P.

  Tilbakestilling Før/Etter

  dette diagrammet viser hva som skjer I Et Kalmanfilter.

  

  kalman filter estimering (kilde)

  • spådd tilstand estimat representerer vår første estimat, vår prediksjon fase. Vi snakker om prior.
  • Måling er måling fra en av våre sensorer. Vi har bedre usikkerhet, men støyen fra sensorene gjør det til en måling som alltid er vanskelig å estimere. Vi snakker om sannsynlighet.
  • Optimal Tilstand Estimat er vår oppdateringsfase. Usikkerheten er denne gangen den svakeste, vi samlet informasjon og fikk lov til å generere en verdi mer sikker enn med vår sensor alene. Denne verdien er vår beste gjetning. Vi snakker om posterior.

  Hva Et Kalman-filter implementerer er faktisk En Bayes-regel.

  

  i et kalmanfilter slår vi spådommer fra målinger. Våre spådommer er alltid mer presise siden vi holder et mål på usikkerhet og regelmessig beregner feilen mellom vår prediksjon og virkelighet. Vi er i stand til fra matrisemultiplikasjoner og sannsynlighetsformler å estimere hastigheter og posisjoner av kjøretøy rundt oss.

  «Utvidede / Uparfymerte» filtre og ikke-linearitet

  et viktig problem oppstår. Våre matematiske formler er alle implementert med lineære funksjoner av type y = ax + b.
  Et Kalmanfilter fungerer alltid med lineære funksjoner. På Den annen side, når Vi bruker En Radar, er dataene ikke lineære.

  

  en radar

  radaren ser verden med tre tiltak:

  disse tre verdiene gjør målingen vår ikke-lineær med tanke på at vinkelen φ er inkludert.

  målet vårt her er å konvertere data ρ, φ, ρ til Kartesisk data (px, py, vx, vy).hvis vi skriver inn ikke-lineære data I Et Kalmanfilter, er resultatet ikke lenger i unimodal Gaussisk form, og vi kan ikke lenger estimere posisjon og hastighet.

  

  Gaussisk vs ikke-linearitet

  så vi bruker tilnærminger, og derfor jobber vi med to metoder:
  – utvidede kalmanfiltre bruker jacobian og taylor-serien til å linearisere modellen.
  – Unscented Kalman filtre bruker en mer presis tilnærming til å linearisere modellen.

  for å håndtere inkludering av ikke-linearitet Av Radar, teknikker eksisterer og tillate våre filtre for å beregne posisjon og hastighet av objektene som vi ønsker å spore.