under noen omstendigheter bidrar strømmen i viklingen av en toroidal induktor bare Til b-feltet inne i viklingene og gir ingen bidrag til det magnetiske b-feltet utenfor viklingene. Dette er en konsekvens av symmetri og Ampè circuital lov.

Tilstrekkelige betingelser for total intern inneslutning Av b-feltetrediger

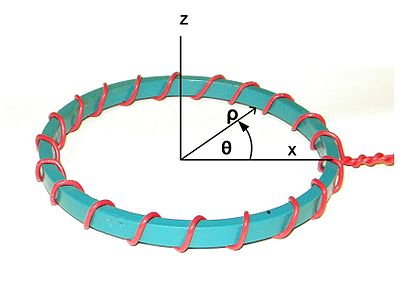fig. 1. Koordinatsystem. Z-aksen er den nominelle symmetriaksen. X-aksen valgt vilkårlig å stille opp med startpunktet for viklingen. ρ kalles radial retning. θ kalles omkretsretningen.

fraværet av omkretsstrøm (banen til omkretsstrøm er indikert med den røde pilen i figur 3 i denne delen) og den aksialt symmetriske utformingen av ledere og magnetiske materialer er tilstrekkelige betingelser for total intern inneslutning Av b-feltet. (Noen forfattere foretrekker Å bruke h-feltet). På grunn av symmetrien må linjene Med b flux danne sirkler med konstant intensitet sentrert på symmetriaksen. De eneste linjene Med b flux som omslutter noen strøm er de som er inne i den toroidale viklingen. Derfor, Fra Ampere ‘ s circuital law, må intensiteten Til b-feltet være null utenfor viklingene.

Fig. 3. Toroidal induktor med omkretsstrøm

Figur 3 i denne delen viser den vanligste toroidale viklingen. Det mislykkes begge kravene for total b felt inneslutning. Ser ut fra aksen, noen ganger er viklingen på innsiden av kjernen, og noen ganger er den på utsiden av kjernen. Det er ikke aksialt symmetrisk i nærområdet. Men på punkter en avstand på flere ganger viklingsavstanden, ser toroiden symmetrisk ut. Det er fortsatt problemet med omkretsstrømmen. Uansett hvor mange ganger viklingen omgir kjernen og uansett hvor tynn ledningen, vil denne toroidale induktoren fortsatt inkludere en spolesløyfe i toroidplanet. Denne viklingen vil også produsere Og være mottakelig for Et e-felt i induktorens plan.

Figur 4-6 viser forskjellige måter å nøytralisere omkretsstrømmen på. Figur 4 er den enkleste og har fordelen at returledningen kan legges til etter at induktoren er kjøpt eller bygget.

Fig. 5. Omkretsstrøm motvirkes med en returvikling.

Fig. 6. Omkretsstrøm motvirkes med en delt returvikling.

Fig. 4. Omkretsstrøm motvirkes med en returledning. Ledningen er hvit og går mellom den ytre kanten av induktoren og den ytre delen av viklingen.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

det vil være en fordeling av potensial langs viklingen. Dette kan føre til Et E-Felt i toroidplanet og også en følsomhet for Et e-felt i toroidplanet som vist i figur 7. Dette kan reduseres ved å bruke en returvikling som vist på figur 8. Med denne viklingen, hvert sted viklingen krysser seg selv, vil de to delene være like og motsatt polaritet som vesentlig reduserer e-feltet generert i flyet.

Toroidal induktor/transformator og magnetisk vektorpotensialrediger

Se Feynman kapittel 14 og 15 for en generell diskusjon av magnetisk vektorpotensial. Se Feynman side 15-11 for et diagram av det magnetiske vektorpotensialet rundt en lang tynn solenoid som også viser total intern inneslutning Av b-feltet, i det minste i uendelig grense.

a-feltet er nøyaktig ved bruk av antagelsen b f a = 0 {\displaystyle bf{a} = 0}

. Dette ville være sant under følgende forutsetninger:

• 1. Coulomb-måleren brukes
• 2. Lorenz-måleren brukes og det er ingen fordeling av ladning, ρ = 0 {\displaystyle \rho =0\,}
  
• 3. Lorenz måleren brukes og null frekvens antas
• 4. Lorenz-måleren brukes og en ikke-null frekvens som er lav nok til å forsømme 1 c 2 ∂ ϕ ∂ t {\displaystyle {\frac {1} {c^{2}} {\frac {\partial \ phi} {\partial t}}
  

  antas.

Nummer 4 vil bli antatt for resten av denne delen og kan bli henvist til «kvasi-statisk tilstand».

Selv om den aksialsymmetriske toroidale induktoren uten omkretsstrøm helt begrenser b-feltet i viklingene, er a-feltet (magnetisk vektorpotensial) ikke begrenset. Pil # 1 på bildet viser vektorpotensialet på symmetriaksen. Radial strøm seksjoner a og b er like avstander fra aksen, men pekte i motsatt retning, slik at de vil avbryte. På samme måte segmenter c og d avbryte. Faktisk alle radial gjeldende segmenter avbryte. Situasjonen for aksiale strømmer er forskjellig. Den aksiale strømmen på utsiden av toroiden peker ned og den aksiale strømmen på innsiden av toroiden peker opp. Hvert aksialt strømsegment på utsiden av toroiden kan matches med et like, men motsatt rettet segment på innsiden av toroiden. Segmentene på innsiden er nærmere enn segmentene på utsiden til aksen, derfor er det en netto oppadgående komponent av a-feltet langs symmetriaksen.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ t → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

) har samme form, så linjene og konturene Til A relaterer Seg Til B som linjene Og konturene Til B relaterer seg til j. dermed er en avbildning av a-feltet rundt en Løkke Av b flux (som det ville bli produsert i en toroidal induktor) er kvalitativt det samme som B-Feltet rundt en strømsløyfe. Figuren til venstre er en kunstners skildring av a-feltet rundt en toroidal induktor. De tykkere linjene indikerer baner med høyere gjennomsnittlig intensitet (kortere baner har høyere intensitet slik at baneintegralet er det samme). Linjene er bare trukket for å se bra ut og gi generelle utseendet På et felt.

Toroidal transformator handling i nærvær av total b felt inneslutning [rediger/rediger Kilde]

e-og b-feltene kan beregnes fra A og ϕ {\displaystyle \phi\,}

(skalar elektrisk potensial) felt B = ∇ × A . {\displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {A} .

og så selv om regionen utenfor Viklingene er blottet for b-felt, er den fylt med ikke-null e-felt. Den mengden ∂ en ∂ t {\displaystyle {\frac {\frac {\partial\mathbf {a}} {\partial t}}}

er ansvarlig for den ønskelige magnetfeltkoblingen mellom primær og sekundær mens mengden ∇ ϕ {\displaystyle \nabla \ phi\,}

er ansvarlig for den uønskede elektriske feltkoblingen mellom primær og sekundær. Transformatordesignere forsøker å minimere den elektriske feltkoblingen. For resten av denne seksjonen vil ∇ ϕ {\displaystyle \nabla \phi\,}

antas å være null med mindre annet er spesifisert. Stokes-teoremet gjelder, slik at baneintegralet Til A er lik den vedlagte b-fluxen, akkurat som baneintegralet B er lik en konstant ganger den vedlagte strømmen

baneintegralet Til E langs sekundærviklingen gir sekundærens induserte EMF (Elektromotivkraft).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

som sier at emf er lik tidsfrekvensen for endring av b-fluxen som er omsluttet av viklingen, som er det vanlige resultatet.

Toroidal transformator Poynting vektorkobling fra primær til sekundær i nærvær av total b feltinneslutning

I denne figuren, blå prikker indikerer hvor b flux fra primærstrømmen kommer ut av bildet og pluss tegn indikerer hvor det går inn i bildet.

forklaring av figurenrediger

denne figuren viser halvdelen av en toroidal transformator. Kvasi-statiske forhold antas, så fasen av hvert felt er overalt det samme. Transformatoren, dens viklinger og alle ting fordeles symmetrisk om symmetriaksen. Viklingene er slik at det ikke er noen omkretsstrøm. Kravene er oppfylt for full intern inneslutning Av b-feltet på grunn av primærstrømmen. Kjernen og primærviklingen er representert av den gråbrune torusen. Primærviklingen vises ikke, men strømmen i viklingen på tverrsnittsflaten vises som gull (eller oransje) ellipser. B-feltet forårsaket av primærstrømmen er helt begrenset til regionen som er omsluttet av primærviklingen (dvs.kjernen). Blå prikker på venstre tverrsnitt indikerer at linjer Med b flux i kjernen kommer ut av venstre tverrsnitt. På det andre tverrsnittet indikerer blå pluss tegn at b-fluxen kommer inn der. E-feltet hentet fra primærstrømmene vises som grønne ellipser. Sekundærviklingen er vist som en brun linje som kommer direkte ned symmetriaksen. I normal praksis er de to ender av sekundæret forbundet sammen med en lang ledning som holder seg godt borte fra torusen, men for å opprettholde den absolutte aksiale symmetrien, er hele apparatet tenkt å være inne i en perfekt ledende sfære med sekundærtråden «jordet» til innsiden av sfæren i hver ende. Sekundæret er laget av motstandstråd, så det er ingen separat belastning. E-feltet langs sekundæret forårsaker strøm i sekundæret (gule piler) som forårsaker Et b-felt rundt sekundæret (vist som blå ellipser). Dette b-feltet fyller plass, inkludert inne i transformatorkjernen, så til slutt er det kontinuerlig Ikke-null b-felt fra primær til sekundær, hvis sekundæret ikke er åpent kretset. Kryssproduktet Av e-feltet (hentet fra primære strømmer) og b-feltet (hentet fra sekundære strømmer) danner Poynting-vektoren som peker fra primær mot sekundær.