en integrert del av væskedynamikken er vorticity. Heuristisk måler den lokal rotasjon av en væskepakke. For faste objekter snakker vi ikke om hvirvelen til et objekt, men i stedet refererer vi til vinkelhastigheten. Disse to konseptene er relaterte, men vorticity er mer nyttig når man diskuterer roterende objekter som deformerer, som en væske gjør.

hvirvelen av et gitt hastighetsfelt innenfor et gitt plan, beregnes ved å velge to ortogonale akser i det planet og legge til vinkelhastigheten til hver akser. I et fast objekt, eller en væske som roterer som et fast objekt (treffende kalt solid legeme rotasjon), er virvelen to ganger vinkelhastigheten siden hver akse roterer med samme hastighet. Men i en væske kan de to aksene rotere med svært forskjellige priser og til og med forskjellige retninger! Det er også mulig at hver akse kan rotere, men nettovortisiteten er null(se irrotasjonsvortex).hvis bevegelsen av en væske er strengt begrenset til å ligge i et plan, blir vortisitetsvektoren tatt for å være ortogonal til flyet og kan ikke endre retninger (eller vippe). Det eneste aspektet av vorticiteten som kan forandre er dens størrelse. Det antas at denne overføringen av energi til større skalaer er forbundet med dannelsen Av Great Red Spot På Jupiter.

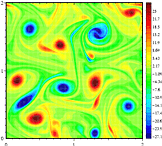
i tredimensjonal væskebevegelse er vortisitetsvektoren tredimensjonal ved at den har komponenter parallelt med hver akse, x, y og z: z-komponenten er parallell med z-aksen og beskriver rotasjonshastigheten i xy-planet. Det er på grunn av denne dikotomi at det er en kvalitativ forskjell i atferd mellom todimensjonal turbulens og tredimensjonal turbulens. I førstnevnte er det en tendens til at virvlene klumper seg sammen og danner større virvler, mens i sistnevnte blir de virvlende bevegelsene revet fra hverandre og energien kaskader ned til de minste skalaer hvor den deretter diffuseres bort.

Matematisk er virvelen til et gitt hastighetsfelt,

er definert som krøllen til hastighetsfeltet, og er vanligvis betegnet med den greske bokstaven omega,

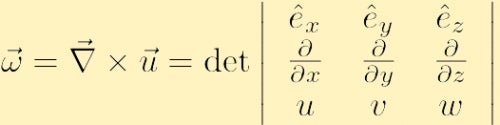
hvor vi har brukt det konvensjonelle nabla-symbolet For Gradienten:

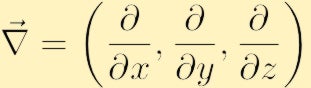
i komponentform er vortisiteten funnet ved å utvide determinanten ovenfor,

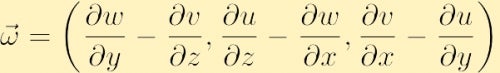
et annet viktig aspekt av væskedynamikk som er relatert til vortisitet er sirkulasjon. I motsetning til virvling som er en lokal egenskap, definert på hvert punkt i rommet, er sirkulasjon en global egenskap, definert ved å integrere en egenskap av væsken over en kurve. Spesielt, hvis du velger en lukket kontur og betegner den Med bokstaven C(t), er sirkulasjonen Rundt C(t), mot urviseren, en skalar mengde betegnet med,

er definert som,

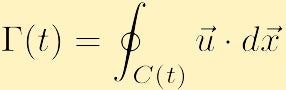
som kan være en funksjon av tid, som kan den lukkede konturen.

La oss ta et øyeblikk for å forklare hva dette sier fysisk. Ved hvert punkt på contourC(t) finner vi komponenten av hastigheten som er tangent til kurven og multipliserer denne skalaren med en uendelig lengde; projisering av hastigheten på tangenten vil nødvendigvis gi en størrelse mellom hastigheten i den posisjonen og null. Hvis hastigheten er tangent til kurven, får vi pluss eller minus hastigheten til, hvis hastigheten er ortogonal til kurven, får vi null. Da integrerer vi denne mengden, en annen måte å si summere et uendelig antall ting, rundt konturen, slik at vi legger til bidraget fra hvert punkt. Fra dette fastslår vi at sirkulasjonen langs en kontur C (t) er mengden strømning rundt konturenc (t); et positivt eller negativt resultat tilsvarer kontur med urviseren eller med urviseren, henholdsvis. Et ekstremt tilfelle er hvor hastighetsfeltet er overalt vinkelrett på kurven C (t), og følgelig er det ingen sirkulasjon siden strømmen alltid krysser konturen og aldri strømmer langs konturen. For å få en ikke-null sirkulasjon må det være en del av kurven der strømmen er langs den lukkede konturen.

Hvis hastighetsfeltet er glatt og Det ikke er noen singulariteter Innen C (t), kan Vi bruke Stokes ‘Integralteorem fra vector calculus for å omskrive sirkulasjonen som,

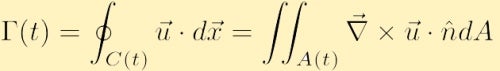
Hvor A er området inneholdt I kontur C og ń er enheten normal vektor til områdetaa.

Før vi vurderer denne nye ligningen for sirkulasjonen, er det nyttig å forstå den fysiske betydningen For Stokes ‘ Teorem hvor vektorfeltet er hastigheten. I det dobbelte integralet ovenfor beregner vi vorticiteten på hvert punkt i konturen og oppsummerer deretter vorticiteten over alle disse punktene I A (t). I enkeltintegralet over den lukkede konturen beregner vi strømmen langs grensen til området. Stokes ‘ teorem sier da at disse mengdene er like, og dermed at hvis det er mean vorticity innenfor et område, som da må bety at området har en ikke-null rotasjonshastighet, må det følgelig være en netto sirkulasjon langs omkretsen av denne grensen.

fra Mean Value Theorem of calculus kan vi erstatte integranden i dobbeltintegralet med en middelverdi, som tilsvarer den gjennomsnittlige komponenten av vorticity ortogonal til flyet Der C(t) ligger. Dermed er den andre tolkningen av sirkulasjon at det er gjennomsnittlig vorticity ganger området inneholdt I C (t). I stedet for å beregne sirkulasjonen På den lukkede konturen C (t) kan vi beregne gjennomsnittlig vorticity normal Til A (t) og multiplisere det med området innenfor. Hvis du vurderer det spesielle tilfellet der hvirvelen er overalt konstant, vil sirkulasjonen være størrelsen på hvirvelen ganger området som finnes i.

en punktvortex er en vortex som ikke har noe område, noe som betyr at vorticity bare er tilstede på et enkelt punkt. For å studere punktvorter vil vi først anta at vi har EN 2d inkompressibel strømning. (Punktvorter er også noen ganger referert til som linjevorter når de ses i 3D.)

etter noen beregninger bestemmer vi at hastighetsfeltet som genereres av et punkt vortex, i kompleks form, som ligger ved z0, er gitt av (Hvor Gamma null er sirkulasjonen rundt punktet vortex, som ofte refereres til som styrken til punktvortex):

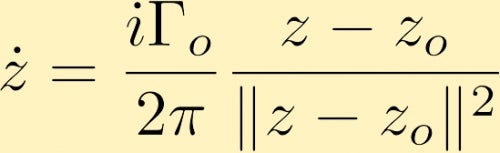
hastighetsfeltet generert av ett punkt vortex kan føre til at et annet punkt vortex beveger seg. Her er noen eksempler på dette: De to punkt virvler, både positive og like stor, de to punkt virvler, både positive, men en har tredoble styrken av den andre og ett punkt vortex er negativ med to ganger størrelsen på den andre som er positiv . En annen mulighet er å vurdere to punkt virvler av samme størrelse, men motsatt fortegn.

Dette kan utvides til et hvilket som helst antall punktvorter, N. bevegelsesligningen i kompleks form for en punktvortex alfa er gitt ved:

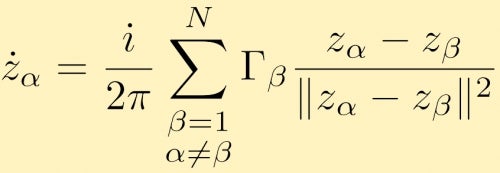
Å Se på samspillet mellom punktvorter er et veldig interessant problem som er vanskelig å gjøre analytisk, spesielt ettersom antall punktvorter øker. Numeriske simuleringer av punkt vortex interaksjoner er dermed svært vanlig. En nyttig anvendelse av store punktvortex simuleringer er hvis du ser på store klynger av punktvorter som simulerer hvirvler med endelig område. Her er beskrivelser og resultatene av flere store punkt vortex simuleringer. I dette tilfellet har vi to store klynger av punktvorter med lik styrke sammenslåing. I neste tilfelle starter vi med en ring av grupperte punkt veracities.

for å finne en ligning for utviklingen av vortisiteten begynner vi med momentumligningen. I momentumligningen kan advektiv termen omskrives som følger,

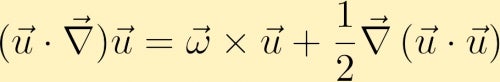
vi beregner deretter krøllen til momentumligningen og gjennom noen vektoridentiteter får vi vortisitetsligningen:

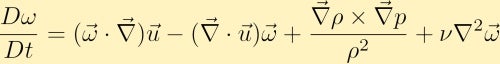
virvelligningen viser hvordan virvel kan genereres i en væske. Uten tap av generalitet vil vi anta at vi i utgangspunktet bare har virvling i z-retningen. Fra dette kan vi se hvordan hver av de fire forskjellige begrepene kan endre vorticiteten.

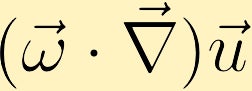
hvis det er en endring i hastighet med retning av eksisterende virvling, kan virvling genereres.

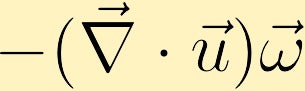
Hvis en væskepakke ekspanderer og virvelen er positiv, vil virvelen av væskepakken reduseres, og hvis pakken kontraherer, vil virvelen øke.

Væskelag med konstant tetthet (isopyknaler) vil falle sammen med lag med konstant trykk (isobarer). Hvis disse lagene ikke faller sammen, begynner væsken å rotere for å få dem til å stå opp, noe som fører til at virvling blir generert. (I eksemplet starter vi med null vorticity.)

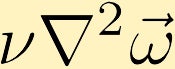
Viskøse krefter forårsaker spredning av virvling. (I eksemplet starter vi med et punkt med uendelig virvling i midten.)