8.2: Wavefunctions
rozwiązania równania Schrödingera z atomem wodoru są funkcjami, które są produktami sferycznej funkcji harmonicznej i funkcji radialnej.
\
funkcje falowe atomu wodoru zależą od trzech zmiennych r, \(\theta\) i \(\varphi \) oraz trzech liczb kwantowych n, \(l\) i \(m_l\). Zmienne podają położenie elektronu względem protonu we współrzędnych sferycznych. Bezwzględny kwadrat funkcji falowej, \ (|\psi (r, \theta, \varphi )|^2\), obliczony w \(r\), \(\theta\) i \(\varphi\) daje gęstość prawdopodobieństwa znalezienia elektronu wewnątrz objętości różniczkowej \(d \tau\), wyśrodkowanej w pozycji określonej przez r, \(\theta\) i \(\varphi\).
ćwiczenie \(\PageIndex{1}\)
Jaka jest wartość całki
\
liczby kwantowe mają nazwy: \(n\) nazywa się główną liczbą kwantową, \(l\) nazywa się liczbą kwantową momentu pędu, a \(m_l\) nazywa się magnetyczną liczbą kwantową, ponieważ(jak zobaczymy w sekcji 8.4) energia w polu magnetycznym zależy od \(m_l\). Często \(l\) nazywa się azymutalną liczbą kwantową, ponieważ jest konsekwencją równania \(\theta\), które obejmuje kąt azymutalny \ (\Theta \), odnoszącego się do kąta do zenitu.
te liczby kwantowe mają określone wartości, które są podyktowane ograniczeniami fizycznymi lub warunkami brzegowymi nałożonymi na równanie Schrödingera: \(n\) musi być liczbą całkowitą większą niż 0, \(l\) może mieć wartości od 0 do n‑1, A \(m_l\) może mieć wartości \(2L + 1\) od \(-l\) ‑ do \(+l\) w krokach jednostkowych lub całkowitych. Wartości liczb kwantowych \(l\) są zwykle kodowane literą: S oznacza 0, p oznacza 1, d oznacza 2, f oznacza 3; kolejne kody kontynuowane są Alfabetycznie (np. g oznacza \(l = 4\)). Liczby kwantowe określają kwantyzację wielkości fizycznych. Dyskretne Energie różnych stanów atomu wodoru są podane przez \(n\), wielkość momentu pędu jest podana przez \(l\), a jeden składnik momentu pędu (zwykle wybrany przez chemików jako składnik z) jest podany przez \(m_l\). Całkowita liczba orbitali o określonej wartości \(n\) to \(N^2\).
ćwiczenie \(\PageIndex{2}\)
rozważmy kilka wartości dla n i pokażemy, że liczba orbitali dla każdego n jest \(N^2\).
ćwiczenie \(\PageIndex{3}\)
skonstruuj tabelę podsumowującą dozwolone wartości dla liczb kwantowych n, \(l\) i \(m_l\). dla poziomów energetycznych od 1 do 7 wodoru.
ćwiczenie \(\PageIndex{4}\)
notacja 3d określa liczby kwantowe elektronu w atomie wodoru. Jakie są wartości dla n i \(l\) ? Jakie są wartości energii i momentu pędu? Jakie są możliwe wartości dla magnetycznej liczby kwantowej? Jakie są możliwe orientacje dla wektora momentu pędu?
fale atomu wodoru, \(\psi (r, \theta , \varphi )\), nazywane są orbitalami atomowymi. Orbital atomowy to funkcja opisująca jeden elektron w atomie. Funkcja falowa z n = 1, \(L=1\) i \(m_l\) = 0 nazywa się orbitalem 1s, a elektron, który jest opisany przez tę funkcję, mówi się, że jest ” w ” orbitalu ls, tj. ma stan orbitalu 1s. Ograniczenia \(n\), \(l)\) i \(m_l\), które są nałożone podczas rozwiązania równania Schrödingera atomu wodoru wyjaśniają, dlaczego istnieje pojedynczy orbital 1s, dlaczego istnieją trzy orbitale 2P, pięć orbitali 3d itp. Zobaczymy, gdy weźmiemy pod uwagę Atomy wielu elektronów w Rozdziale 9, że te ograniczenia wyjaśniają cechy układu okresowego. Innymi słowy, układ okresowy jest przejawem modelu Schrödingera i fizycznych ograniczeń nałożonych na uzyskanie rozwiązań równania Schrödingera dla atomu wodoru.
Wizualizacja zmiany funkcji falowej za pomocą \(r\), \(\theta\) i \(\varphi\) jest ważna, ponieważ bezwzględny kwadrat funkcji falowej przedstawia rozkład ładunku (gęstość prawdopodobieństwa elektronu) w atomie lub cząsteczce. Rozkład ładunku ma kluczowe znaczenie dla chemii, ponieważ jest związany z reaktywnością chemiczną. Na przykład, część z niedoborem elektronów jednej cząsteczki jest przyciągana do regionu bogatego w elektrony innej cząsteczki, i takie interakcje odgrywają główną rolę w oddziaływaniach chemicznych, począwszy od reakcji podstawienia i dodawania do fałdowania białek i interakcji substratów z enzymami.
Wizualizacja funkcji falowych i rozkładów ładunków jest trudna, ponieważ wymaga zbadania zachowania funkcji trzech zmiennych w przestrzeni trójwymiarowej. Ta wizualizacja jest łatwiejsza, biorąc pod uwagę części promieniowe i kątowe oddzielnie, ale rysowanie osobno części promieniowych i kątowych nie ujawnia kształtu orbity bardzo dobrze. Kształt można lepiej ujawnić na wykresie gęstości prawdopodobieństwa. Aby stworzyć taki trójwymiarowy wykres, podziel przestrzeń na małe elementy objętości, Oblicz \(\psi^* \psi\) w środku każdego elementu objętości, a następnie odcień, stiple lub kolor tego elementu objętości proporcjonalnie do wielkości \(\psi^* \psi \). Nie myl takich działek z polarnymi działkami, które wyglądają podobnie.
gęstości prawdopodobieństwa mogą być również reprezentowane przez mapy konturowe, jak pokazano na rysunku \(\PageIndex{1}\).
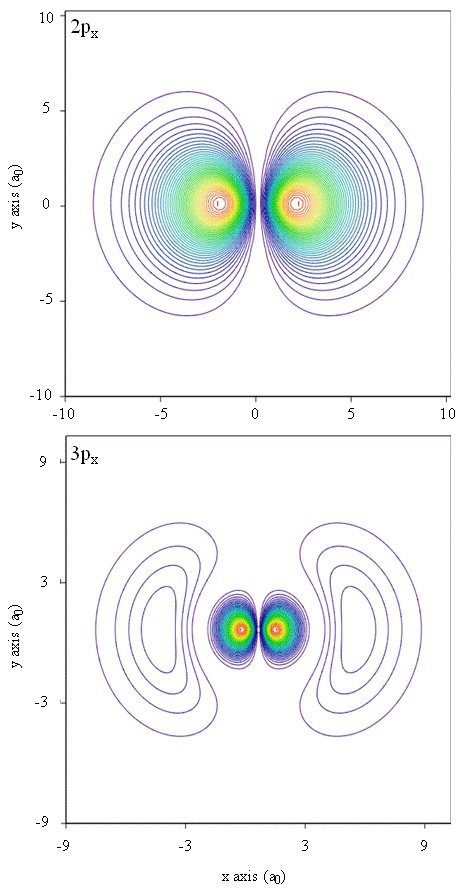
inna technika reprezentacyjna, modelowanie rzeczywistości wirtualnej, posiada wiele obietnic dla reprezentacji gęstości elektronów. Wyobraźcie sobie na przykład możliwość doświadczania gęstości elektronów Jako siły lub oporu na różdżce, którą poruszacie się w przestrzeni trójwymiarowej. Urządzenia takie jak te, zwane urządzeniami haptycznymi, już istnieją i są używane do reprezentowania informacji naukowej. Podobnie, czy nie byłoby interesujące „latać” przez orbital atomowy i doświadczać zmian gęstości elektronów Jako zmiany koloru lub zmiany zachmurzenia? Specjalnie zaprojektowane pomieszczenia z ekranami 3D i” inteligentnymi ” okularami, które dostarczają informacji zwrotnej o kierunku spojrzenia widza, są obecnie opracowywane, aby umożliwić nam doświadczanie takich wrażeń.
metody oddzielnego badania promieniowych części orbitali atomowych dostarczają użytecznych informacji na temat rozkładu gęstości ładunku wewnątrz orbitali. Wykresy funkcji promieniowych, \(R (r)\), dla orbitali 1s, 2s i 2P wykreślonych na rysunku \(\PageIndex{2}\).
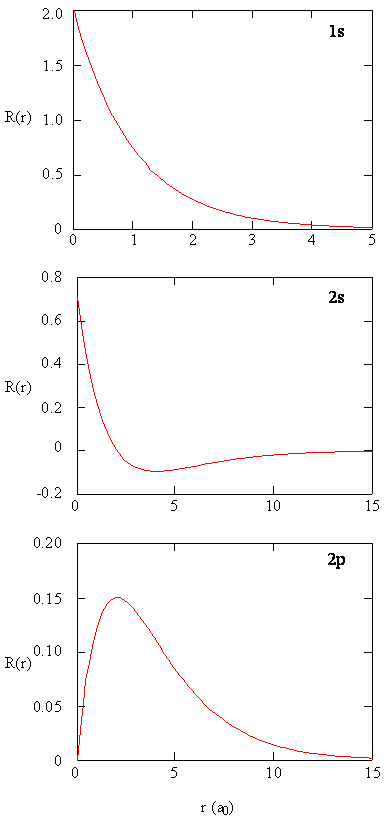
funkcja 1s na rysunku \(\PageIndex{2}\) zaczyna się od wysokiej wartości dodatniej w jądrze i wykładniczo rozpada się do zera po 5 promieniach Bohra. Wysoka wartość w jądrze może być zaskakująca, ale jak zobaczymy później, prawdopodobieństwo znalezienia elektronu w jądrze jest Znikające małe.
następnie zauważ, jak funkcja radialna dla orbitalu 2s, figura \(\PageIndex{2}\), idzie do zera i staje się ujemna. Takie zachowanie ujawnia obecność węzła radialnego w funkcji. Węzeł radialny występuje, gdy funkcja radialna jest równa zeru innym niż \(r = 0\) LUB \(r = ∞\). Węzły i ograniczające zachowania atomowych funkcji orbitalnych są przydatne w identyfikacji, który orbital jest opisywany przez który przebieg. Na przykład, wszystkie funkcje s mają niezerowe wartości funkcji falowej przy \(r = 0\), ale p, d, f i wszystkie inne funkcje idą do zera na początku. Warto pamiętać, że istnieją \(n-1-l\) węzły promieniowe w funkcji falowej, co oznacza, że orbital 1s nie ma węzłów promieniowych, 2s ma jeden węzeł promieniowy i tak dalej.
ćwiczenie \(\PageIndex{5}\)
zbadaj matematyczne formy fal promieniowych. Jaka funkcja w funkcjach powoduje, że niektóre z nich idą do zera w punkcie początkowym, podczas gdy funkcje s nie idą do zera w punkcie początkowym?
ćwiczenie \(\PageIndex{6}\)
jaka funkcja matematyczna każdej z funkcji promieniowych kontroluje liczbę węzłów promieniowych?
ćwiczenie \(\PageIndex{7}\)
przy jakiej wartości R występuje węzeł radialny 2S?
ćwiczenie \(\PageIndex{8}\)
Tworzenie tabeli zawierającej energię, liczbę węzłów promieniowych oraz liczbę węzłów kątowych i całkowitą liczbę węzłów dla każdej funkcji z n = 1, 2 i 3. Określ zależność między energią a liczbą węzłów. Określ zależność między liczbą węzłów promieniowych a liczbą węzłów kątowych.
ilość \(R (r) ^* R(r)\) daje gęstość prawdopodobieństwa radialnego; tj. gęstość prawdopodobieństwa dla elektronu w punkcie znajdującym się w odległości \(r\) od protonu. Radialne gęstości prawdopodobieństwa dla trzech typów orbitali atomowych są wykreślone na rysunku (\PageIndex{3}\).
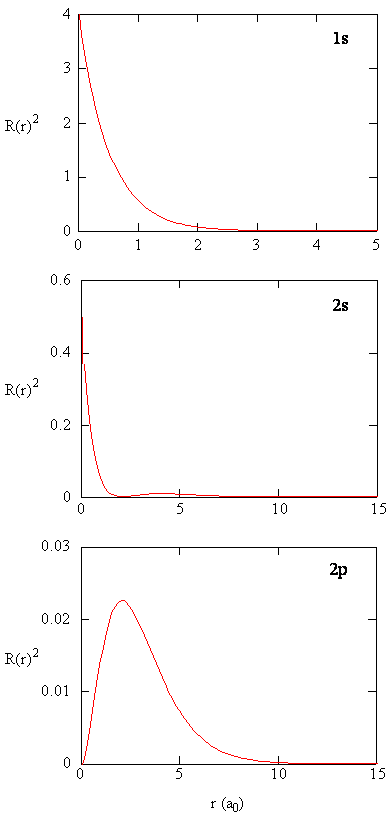
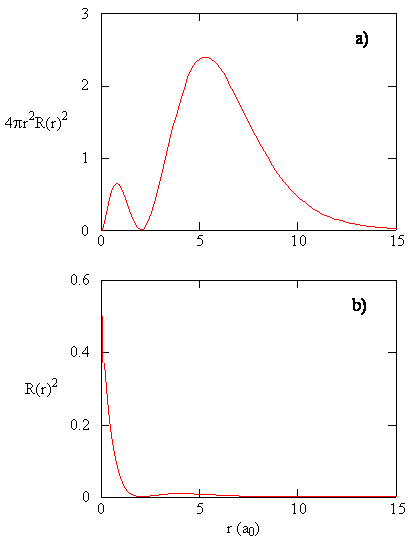
gdy gęstość prawdopodobieństwa radialnego dla każdej wartości r jest pomnożona przez pole powierzchni sferycznej reprezentowane przez tę konkretną wartość r, otrzymujemy funkcję rozkładu radialnego. Funkcja rozkładu radialnego daje gęstość prawdopodobieństwa, że elektron znajdzie się w dowolnym miejscu na powierzchni kuli znajdującej się w odległości r od protonu. Ponieważ pole powierzchni sferycznej wynosi \(4 \ pi R^2\), funkcja rozkładu radialnego jest określona przez \(4 \ pi R^2 R(r) ^* R (R)\).
funkcje rozkładu promieniowego są pokazane na rysunku \(\PageIndex{4}\). Przy małych wartościach r funkcja rozkładu promieniowego jest niska, ponieważ mała powierzchnia dla małych promieni moduluje wysoką wartość radialnej funkcji gęstości prawdopodobieństwa w pobliżu jądra. Gdy zwiększamy \(r\), pole powierzchni związane z podaną wartością r wzrasta, a termin \(r^2\) powoduje wzrost funkcji rozkładu radialnego, mimo że gęstość prawdopodobieństwa radialnego zaczyna się zmniejszać. Przy dużych wartościach \(r\) wykładniczy rozpad funkcji radialnej przeważa nad wzrostem wywołanym przez \(r^2\), a funkcja rozkładu radialnego zmniejsza się.
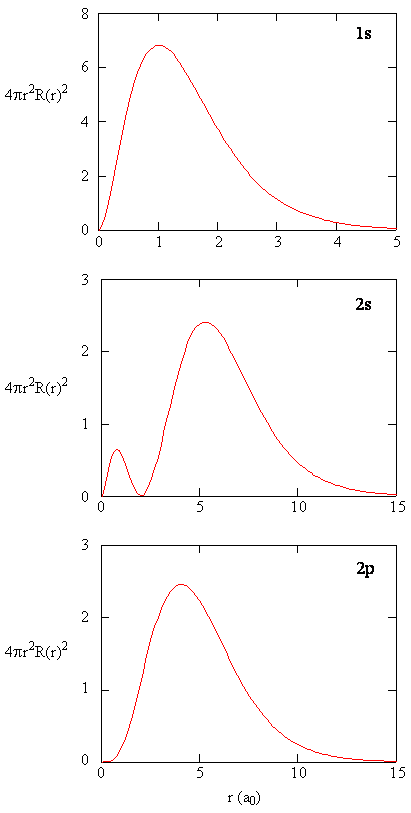
ćwiczenie \(\PageIndex{9}\)
napisz porównanie jakości funkcji radialnej i funkcji rozkładu radialnego dla orbitalu 2S. Zobacz rysunek (\PageIndex{5}\)
autorzy i atrybuty
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zieliński („Stany kwantowe atomów i cząsteczek”)