Toroidalne induktory i transformatory
w pewnych okolicznościach prąd w uzwojeniu cewki toroidalnej przyczynia się tylko do pola B wewnątrz uzwojeń i nie przyczynia się do pola magnetycznego B poza uzwojeniami. Jest to konsekwencja symetrii i prawa obwodowego Ampère ’ a.
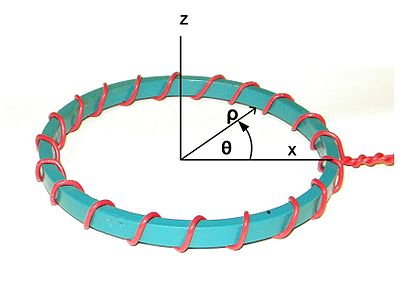
rys. 1. Układ współrzędnych. Oś Z jest nominalną osią symetrii. Oś X wybrana arbitralnie w celu wyrównania z punktem początkowym uzwojenia. ρ nazywa się kierunkiem radialnym. θ nazywa się kierunkiem obwodowym.
|
 rys. 2. Osiowo symetryczny induktor toroidalny bez prądu obwodowego.
|
brak prądu obwodowego (ścieżkę prądu obwodowego wskazuje czerwona strzałka na rysunku 3 w tej sekcji) oraz osiowo symetryczny układ przewodników i materiałów magnetycznych są wystarczającymi warunkami do całkowitego wewnętrznego zamknięcia pola B. (Niektórzy autorzy wolą używać pola H). Ze względu na symetrię linie strumienia B muszą tworzyć okręgi o stałym natężeniu wyśrodkowane na osi symetrii. Jedynymi liniami strumienia B, które otaczają dowolny prąd, są te, które znajdują się wewnątrz uzwojenia toroidalnego. Dlatego też, zgodnie z prawem obwodowym Ampere ’ a, natężenie pola B musi być zerowe poza uzwojeniami.

Rysunek 3 przedstawia najczęściej spotykane uzwojenie toroidalne. Nie spełnia obu wymagań dotyczących całkowitego ograniczenia pola B. Patrząc z osi, czasami uzwojenie znajduje się wewnątrz rdzenia, a czasami Na Zewnątrz rdzenia. Nie jest osiowo symetryczny w bliskim regionie. Jednak w punktach znajdujących się w odległości kilkukrotnego odstępu od nawijania toroid wygląda symetrycznie. Nadal istnieje problem prądu obwodowego. Bez względu na to ile razy uzwojenie otacza rdzeń i bez względu na to jak cienki jest drut, induktor ten nadal będzie zawierał jedną pętlę cewki w płaszczyźnie toroidu. Uzwojenie to będzie również wytwarzało i było podatne na działanie pola E w płaszczyźnie induktora.
rysunki 4-6 pokazują różne sposoby neutralizacji prądu obwodowego. Rysunek 4 jest najprostszy i ma tę zaletę, że przewód powrotny można dodać po zakupie lub zbudowaniu cewki indukcyjnej.
 rys. 4. Prąd obwodowy przeciwdziała przewodem powrotnym. Przewód jest biały i biegnie między zewnętrzną krawędzią cewki a zewnętrzną częścią uzwojenia.
|
 rys. 5. Prąd obwodowy przeciwdziała uzwojeniu powrotnemu.
|
 rys. 6. Prąd obwodowy przeciwdziała z uzwojeniem powrotnym dzielonym.
|
- E field in the plane of the toroidEdit
- toroidalny induktor/transformator i magnetyczny wektor potencjałedytuj
- działanie transformatora toroidalnego w obecności całkowitego ograniczenia pola Bedit
- transformator toroidalny sprzężenie wektorowe z pierwotnego do wtórnego w obecności całkowitego ograniczenia pola Bedit
- Wyjaśnienie rysunkuedytuj
E field in the plane of the toroidEdit
 Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.
|
 Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.
|
będzie rozkład potencjału wzdłuż uzwojenia. Może to prowadzić do powstania POLA E w płaszczyźnie toroidu, a także do podatności na pole E w płaszczyźnie toroidu, jak pokazano na fig. Można to złagodzić za pomocą uzwojenia powrotnego, jak pokazano na rysunku 8. Przy tym uzwojeniu, każde miejsce uzwojenia przecina się, dwie części będą miały równą i przeciwną polaryzację, co znacznie zmniejsza pole e generowane w płaszczyźnie.
toroidalny induktor/transformator i magnetyczny wektor potencjałedytuj

ogólne omówienie magnetycznego potencjału wektorowego znajduje się w rozdziale 14 i 15 Feynmana. Patrz strona Feynmana 15-11 dla diagramu potencjału wektora magnetycznego wokół długiego cienkiego elektromagnesu, który również wykazuje całkowite wewnętrzne ograniczenie pola B, przynajmniej w nieskończonej granicy.
pole a jest dokładne przy założeniu b f A = 0 {\displaystyle bf{a}=0}

. Byłoby to zgodne z następującymi założeniami:
- 1. zastosowano miernik Coulomba
- 2. używany jest wskaźnik Lorenza i nie ma rozkładu ładunku, ρ =0 {\displaystyle \rho=0\,}
- 3. stosuje się wskaźnik Lorenza i przyjmuje się częstotliwość zerową
- 4. używany jest wskaźnik Lorenza i przyjmuje się niezerową częstotliwość, która jest wystarczająco niska, aby zaniedbać 1 c 2 ∂ ϕ ∂ t {\displaystyle {\frac {1}{C^{2}}}{\frac {\partial \Phi }{\partial t}}}
.
Liczba 4 będzie zakładana dla reszty tej sekcji i może być odnoszona do „warunku quasi-statycznego”.
chociaż osiowo symetryczny induktor toroidalny bez prądu obwodowego całkowicie ogranicza pole B w uzwojeniach, pole a (magnetyczny potencjał wektorowy) nie jest ograniczone. Strzałka # 1 Na zdjęciu przedstawia potencjał wektorowy na osi symetrii. Promieniste odcinki prądu a i b są równe odległości od osi, ale skierowane w przeciwnych kierunkach, więc będą się anulować. Podobnie segmenty c i d się anulują. W rzeczywistości wszystkie segmenty prądu promieniowego anulują się. Sytuacja dla prądów osiowych jest inna. Prąd osiowy po zewnętrznej stronie toroidu jest skierowany w dół, a prąd osiowy po wewnętrznej stronie toroidu jest skierowany w górę. Każdy segment prądu osiowego na zewnątrz toroidu może być dopasowany do równego, ale przeciwstawnie skierowanego segmentu wewnątrz toroidu. Segmenty wewnątrz są bliżej niż segmenty na zewnątrz do osi, dlatego istnieje siatkowa składowa pola a w górę wzdłuż osi symetrii.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ T → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

) mają tę samą formę, wtedy linie i kontury a odnoszą się do B, podobnie jak linie i kontury B odnoszą się do j. strumień B (jaki byłby wytwarzany w induktorze toroidalnym) jest jakościowo taki sam jak Pole B wokół pętli prądu. Rysunek po lewej stronie przedstawia pole A wokół cewki toroidalnej. Grubsze linie oznaczają ścieżki o wyższej średniej intensywności (krótsze ścieżki mają większą intensywność, tak że Całka ścieżki jest taka sama). Linie są po prostu rysowane, aby dobrze wyglądać i nadawać ogólny wygląd pola A.
działanie transformatora toroidalnego w obecności całkowitego ograniczenia pola Bedit
POLA E i B można obliczyć z pól a i ϕ {\displaystyle \phi\,}

(skalarny potencjał elektryczny) B = ∇ × A . {\displaystyle \ mathbf {B} = \ nabla \ times \ mathbf {a} .}

I : E = − ∇ ϕ − ∂ a ∂ t {\displaystyle \mathbf {e} =-\nabla \Phi -{\frac {\partial \mathbf {a} }{\partial t}}}

i tak nawet jeśli obszar poza uzwojeniami jest pozbawiony pola B, to jest wypełniony niezerowym polem E. Ilość ∂ a ∂ t {\displaystyle {\frac {\partial \mathbf {a} }{\partial t}}}

odpowiada za pożądane sprzężenie pola magnetycznego między pierwotnym i wtórnym, podczas gdy ilość ∇ ϕ {\displaystyle \nabla \Phi\,}

jest odpowiedzialny za niepożądane sprzężenie pola elektrycznego między pierwotnym i wtórnym. Projektanci transformatorów próbują zminimalizować sprzężenie pola elektrycznego. W pozostałej części tej sekcji, ∇ ϕ {\displaystyle \nabla \Phi\,}

zostanie przyjęte jako zero, o ile nie określono inaczej.
stosuje się twierdzenie Stokesa, tak że Całka ścieżki A jest równa zamkniętemu przepływowi B, tak jak Całka ścieżki B jest równa stałej razy prąd zamknięty
Całka ścieżki e wzdłuż uzwojenia wtórnego daje indukowaną wtórną siłę EMF (Electro-Motive Force).
E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

który mówi, że EMF jest równy szybkości zmiany strumienia B zamkniętego przez uzwojenie, co jest zwykle wynikiem.
transformator toroidalny sprzężenie wektorowe z pierwotnego do wtórnego w obecności całkowitego ograniczenia pola Bedit

Wyjaśnienie rysunkuedytuj
ten rysunek pokazuje pół przekroju transformatora toroidalnego. Przyjmuje się warunki Quasi-statyczne, więc Faza każdego pola jest wszędzie taka sama. Transformator, jego uzwojenia i wszystkie rzeczy są rozmieszczone symetrycznie wokół osi symetrii. Uzwojenia są takie, że nie ma prądu obwodowego. Wymagania są spełnione dla pełnego wewnętrznego zamknięcia pola B ze względu na prąd pierwotny. Rdzeń i uzwojenie pierwotne są reprezentowane przez szaro-brązowy torus. Uzwojenie pierwotne nie jest pokazane, ale prąd w uzwojeniu na powierzchni przekroju jest pokazany jako złote (lub pomarańczowe) elipsy. Pole B spowodowane prądem pierwotnym jest całkowicie ograniczone do obszaru zamkniętego przez uzwojenie pierwotne (tj. rdzeń). Niebieskie kropki na przekroju lewej ręki wskazują, że linie strumienia B w rdzeniu wychodzą z przekroju lewej ręki. Na drugim przekroju niebieskie znaki plus wskazują, że strumień B wchodzi tam. Pole E pochodzące z prądów pierwotnych przedstawia się jako zielone elipsy. Uzwojenie wtórne jest pokazane jako brązowa linia opadająca bezpośrednio do osi symetrii. W normalnej praktyce dwa końce wtórnego są połączone długim drutem, który pozostaje daleko od torusa, ale aby zachować absolutną symetrię osiową, całe urządzenie jest wyobrażone jako znajdujące się wewnątrz doskonale przewodzącej kuli, z drutem wtórnym „uziemionym” do wnętrza kuli na każdym końcu. Wtórny jest wykonany z drutu oporowego, więc nie ma oddzielnego obciążenia. Pole e wzdłuż wtórnika powoduje prąd w wtórniku (żółte strzałki), co powoduje pole B wokół wtórnika (pokazane jako niebieskie elipsy). To pole B wypełnia przestrzeń, również wewnątrz rdzenia transformatora, więc w końcu istnieje ciągłe niezerowe pole B od pierwotnego do wtórnego, jeśli wtórne nie jest otwarte. Iloczyn krzyżowy POLA E (pochodzącego z prądów pierwotnych) i pola B (pochodzącego z prądów wtórnych) tworzy wektor Poyntinga, który wskazuje od pierwotnego do wtórnego.

