8.2: The Wavefunctions
The solutions to the hydrogen atom Schrödinger equation are functions that are products of a spherical harmonic function and a radial function.
\
O wavefunctions para o átomo de hidrogênio dependem de três variáveis r, \(\theta\) e \(\varphi \) e os três números quânticos n, \(l\) e \(m_l\). As variáveis dão a posição do elétron em relação ao Próton em coordenadas esféricas. O absoluto praça da wavefunction, \(| \psi (r, \theta , \varphi )|^2\), avaliada em \(r\), \(\theta \) e \(\varphi\) dá a densidade de probabilidade de encontrar o elétron dentro de um diferencial de volume \(d \tau\), centrado na posição especificada por r \(\theta \) e \(\varphi\).
Exercício de \(\PageIndex{1}\)
Qual é o valor da integral
\
Os números quânticos têm nomes: \(n\) é chamado o número quântico principal, \(l\) é chamado o número quântico de momento angular, e \(m_l\) é chamado o número quântico magnético porque (como veremos na secção 8.4) a energia num campo magnético depende de \(m_l\). Muitas vezes \(l\) é chamado de número quântico azimutal porque é uma consequência da equação \(\theta\), que envolve o ângulo azimutal \(\Theta \), referindo-se ao ângulo do zênite.
estes números quânticos têm valores específicos que são ditados pelas restrições físicas ou condições de contorno impostas à equação de Schrödinger.: \(n\) deve ser um número inteiro maior que 0, \(l\) pode ter os valores 0 a n‑1, e \(m_l\) pode ter \(2l + 1\) valores variando de \(l\) para \(+l\) na unidade ou o número inteiro passos. Os valores do número quântico \(l\) geralmente são codificadas por uma letra: s significa 0, p, 1, d significa 2, f significa 3; os códigos próximos continuar em ordem alfabética (por exemplo, g significa \(l = 4\)). Os números quânticos especificam a quantização de quantidades físicas. O discreto energias de diferentes estados do átomo de hidrogênio é dado por \(n\), a magnitude do momento angular é dada por \(l\), e um componente do momento angular (geralmente escolhidas pelos químicos para ser o componente‑z) é dado por \(m_l\). O número total de orbitais com um valor particular de \(n\) é \(n^2\).
exercício \(\PageIndex{2}\)
considere vários valores para n, e mostre que o número de orbitais para cada n é \(n^2\).
exercício \(\PageIndex{3}\)
construa uma tabela resumindo os valores permitidos para os números quânticos n, \(l\) e \(m_l\). para os níveis de energia 1 a 7 de hidrogénio.
exercício \(\PageIndex{4}\)
a notação 3d especifica os números quânticos para um electrão no átomo de hidrogénio. Quais são os valores para n e \(l\)? Quais são os valores para a energia e Momento angular? Quais são os valores possíveis para o número quântico magnético? Quais são as possíveis orientações para o vetor momento angular?
the hydrogen atom wavefunctions, \(\psi (r, \theta , \varphi)\), are called atomic orbitals. Uma orbital atômica é uma função que descreve um elétron em um átomo. A função de onda com n = 1, \(l=1\), e \(m_l\) = 0 é chamada de orbital 1s, e um elétron que é descrito por esta função é dito ser “no orbital ls, ou seja, tem um estado orbital 1s. As restrições em \(n\), \(l)\) e \(m_l\) que são impostas durante a solução do átomo de hidrogênio equação de Schrödinger explicar porque não existe um único orbital 1s, por isso que existem três orbitais 2p, cinco orbitais 3d, etc. Veremos quando considerarmos os átomos multi-elétrons no Capítulo 9 que estas restrições explicam as características Da Tabela Periódica. Em outras palavras, a Tabela Periódica é uma manifestação do modelo de Schrödinger e as restrições físicas impostas para obter as soluções para a equação de Schrödinger para o átomo de hidrogênio.
visualizando a variação de uma função de onda eletrônica com \(r\), \(\theta\), e \(\varphi\) é importante porque o quadrado absoluto da função de onda retrata a distribuição de carga (densidade de probabilidade de elétrons) em um átomo ou molécula. A distribuição de carga é central para a química porque está relacionada à reatividade química. Por exemplo, uma parte deficiente de elétrons de uma molécula é atraída para uma região rica em elétrons de outra molécula, e tais interações desempenham um papel importante em interações químicas que vão desde reações de substituição e adição a dobragem de proteínas e a interação de substratos com enzimas.
Visualizando funções de onda e distribuições de carga é um desafio porque requer examinar o comportamento de uma função de três variáveis no espaço tridimensional. Esta visualização é facilitada considerando as partes radial e angular separadamente, mas plotar as partes radial e angular separadamente não revela a forma de um orbital muito bem. A forma pode ser revelada melhor em um gráfico de densidade de probabilidade. Para fazer tal tridimensional do terreno, dividir o espaço em um volume reduzido de elementos, calcular \(\psi^* \psi \) no centro de cada elemento de volume e, em seguida, a sombra, a stipple ou a cor que o volume do elemento, em proporção à magnitude de \(\psi^* \psi \). Não confunda tais parcelas com parcelas polares, que parecem semelhantes.
densidades de probabilidade também podem ser representadas por mapas de contorno, como mostrado na figura \(\PageIndex{1}\).
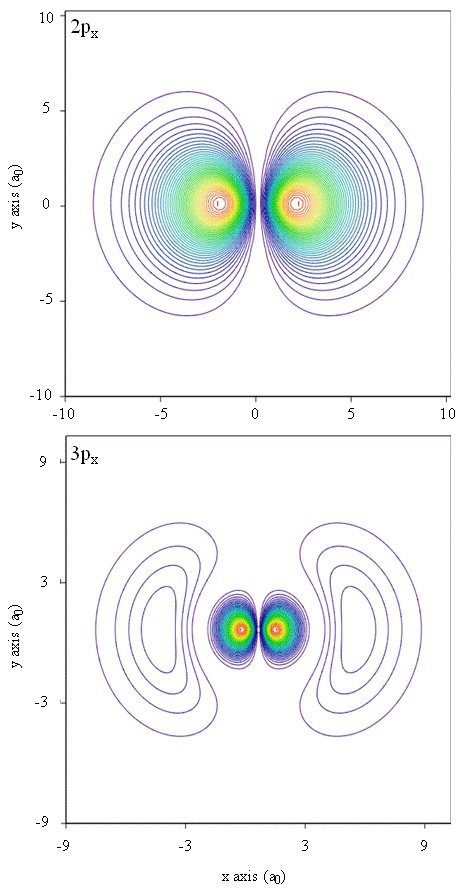
outra técnica de representação, modelagem de Realidade virtual, detém uma grande promessa de representação de densidades elétricas. Imagine, por exemplo, ser capaz de experimentar a densidade de elétrons como uma força ou resistência em uma varinha que você move através do espaço tridimensional. Dispositivos como estes, chamados dispositivos hápticos, já existem e estão sendo usados para representar informações científicas. Da mesma forma, não seria interessante “voar” através de um orbital atômico e experimentar mudanças na densidade de elétrons como mudanças de cor ou mudanças de nebulosidade? Salas especialmente projetadas com telas 3D e óculos “inteligentes” que fornecem feedback sobre a direção do olhar do espectador estão sendo desenvolvidos atualmente para nos permitir experimentar tais sensações.
métodos para examinar separadamente as porções radiais dos orbitais atômicos fornecem informações úteis sobre a distribuição da densidade de carga dentro dos orbitais. Grafos das funções radiais, \(R (r)\), para os orbitais 1s, 2s e 2p plotados na figura \(\PageIndex{2}\).
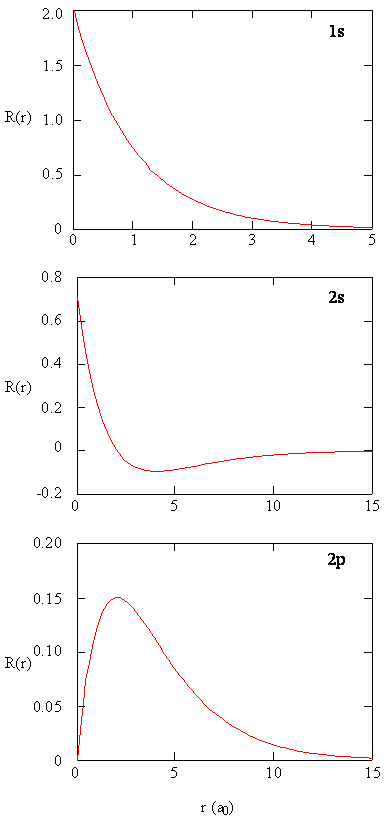
O 1s função na Figura \(\PageIndex{2}\) começa com um alto valor positivo no núcleo e decai exponencialmente para zero depois de 5 raios de Bohr. O alto valor no núcleo pode ser surpreendente, mas como veremos mais tarde, a probabilidade de encontrar um elétron no núcleo é muito pequena.
próxima observação de como a função radial para o orbital 2s, figura \(\PageIndex{2}\), vai para zero e torna-se negativo. Este comportamento revela a presença de um nó radial na função. Um nó radial ocorre quando a função radial é igual a zero, exceto em \(r = 0\) ou \(r=∞\). Nós e comportamentos limitantes das funções orbitais atômicas são ambos úteis na identificação de qual orbital está sendo descrito por qual função de onda. Por exemplo, todas as funções s têm valores de função de onda não-zero em \(r = 0\), mas p, d, f e todas as outras funções vão para zero na origem. É útil lembrar que existem nós radiais \(n-1-L\) em uma função de onda, o que significa que um orbital 1s não tem nós radiais, um 2s tem um nó radial, e assim por diante.
exercício \(\PageIndex{5}\)
Examine as formas matemáticas das ondulações radiais. Que característica nas funções faz com que alguns deles vão para zero na origem, enquanto as funções s não vão para zero na origem?
exercício \(\PageIndex{6}\)
Que característica matemática de cada uma das funções radiais controla o número de nós radiais?
exercício \(\PageIndex{7}\)
a que valor de r ocorre o nó radial 2s?
exercício \(\PageIndex{8}\)
Faça uma tabela que forneça a energia, o número de nós radiais, e o número de nós angulares e o número total de nós para cada função com n = 1, 2 e 3. Identificar a relação entre a energia e o número de nós. Identificar a relação entre o número de nós radiais e o número de nós angulares.
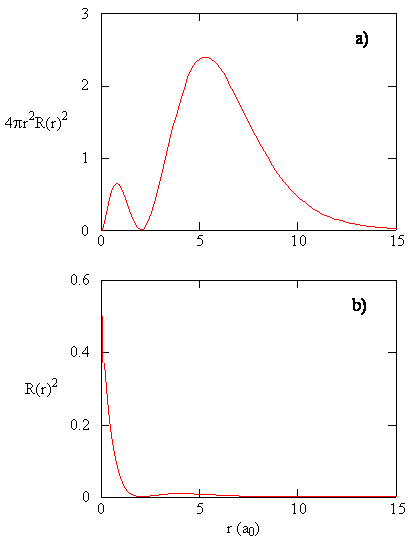
a quantidade \(R (r) ^ * R (r)\) dá a densidade de probabilidade radial; ou seja, a densidade de probabilidade para o elétron estar em um ponto localizado a distância \(r\) do próton. Densidades de probabilidade Radial para três tipos de orbitais atômicos são plotadas na figura (\PageIndex{3}\).
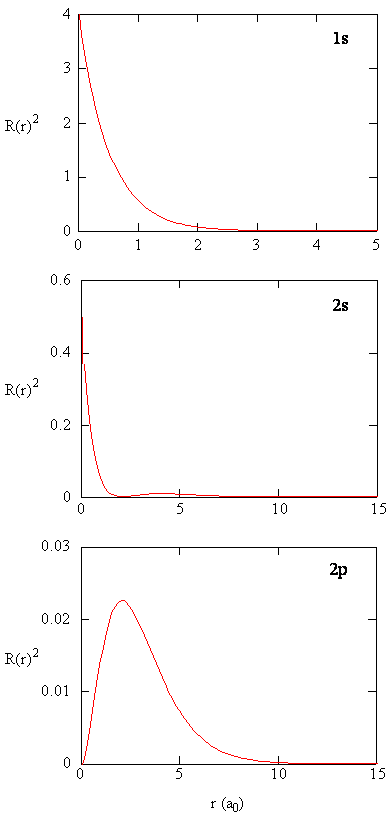
quando a densidade de probabilidade radial para cada valor de r é multiplicada pela área da superfície esférica representada por esse valor particular de r, obtém-se a função de distribuição radial. A função de distribuição radial dá a densidade de probabilidade de um elétron ser encontrado em qualquer lugar na superfície de uma esfera localizada a uma distância r do próton. Uma vez que a área de uma superfície esférica é \(4 \pi r^2\), a função de distribuição radial é dada por \(4 \pi r^2 R(r) ^* R(r)\).
as funções de distribuição Radial são mostradas na figura \(\PageIndex{4}\). Em pequenos valores de r, A função de distribuição radial é baixa porque a pequena área de superfície para pequenos raios modula o alto valor da função de densidade de probabilidade radial perto do núcleo. À medida que aumentamos \(r\), a área de superfície associada a um dado valor de R aumenta, e o termo \(R^2\) faz com que a função de distribuição radial aumente, mesmo que a densidade de probabilidade radial esteja começando a diminuir. Em grandes valores de \(r\), o decaimento exponencial da função radial supera o aumento causado pelo termo \(R^2\) e a função de distribuição radial diminui.
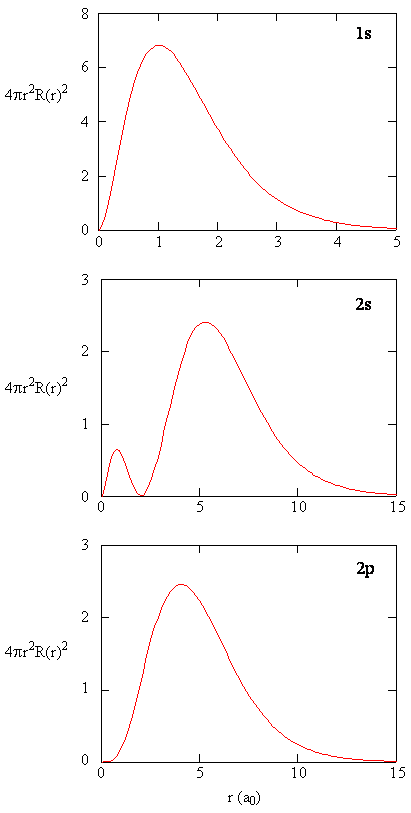
Exercise \(\PageIndex{9}\)
Write a quality comparison of the radial function and radial distribution function for the 2s orbital. Veja a Figura (\PageIndex{5}\)
Colaboradores e Atribuições
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (“Estados Quânticos dos Átomos e Moléculas”)