Em algumas circunstâncias, a corrente no enrolamento do indutor toroidal, contribui apenas para o campo B no interior dos enrolamentos e não faz nenhuma contribuição para o magnético B campo fora dos enrolamentos. Esta é uma consequência da simetria e da lei circuital de Ampère.

Suficientes condições para a interna total confinamento do B fieldEdit

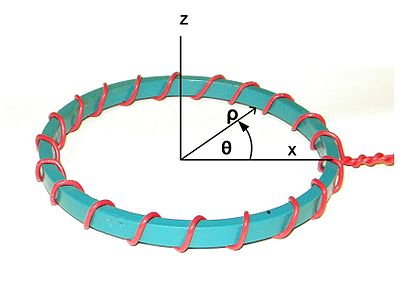Fig. 1. Coordenada. O eixo Z é o eixo nominal de simetria. O eixo X escolhido arbitrariamente para se alinhar com o ponto de partida do enrolamento. ρ é chamada de direção radial. θ é chamado de direção circunferencial.

Fig. 2. Um indutor toroidal axial simétrico sem corrente circunferencial.

A ausência de circunferencial atual (o caminho da circunferencial actual é indicado pela seta vermelha na figura 3 desta seção) e axialmente simétrica disposição dos condutores e materiais magnéticos são suficientes condições para a interna total confinamento do campo B. (Alguns autores preferem usar o campo H). Por causa da simetria, as linhas do fluxo B devem formar círculos de intensidade constante centrados no eixo de simetria. As únicas linhas de fluxo B que rodeiam qualquer corrente são as que estão dentro do enrolamento toroidal. Portanto, a partir da lei circuital de Ampere, a intensidade do campo B deve ser zero fora dos enrolamentos.

Fig. 3. O indutor Toroidal com corrente circunferencial

Figura 3 desta secção mostra o enrolamento toroidal mais comum. Falha em ambos os requisitos para o confinamento total de campo B. Olhando para fora do eixo, às vezes o enrolamento está no interior do núcleo e às vezes está no exterior do núcleo. Não é axialmente simétrica na região próxima. No entanto, em pontos a uma distância de várias vezes o espaçamento enrolamento, o toróide parece simétrico. Há ainda o problema da corrente circunferencial. Não importa quantas vezes o enrolamento circunda o núcleo e não importa o quão fino o fio, este indutor toroidal ainda incluirá um laço de uma bobina no plano do toróide. Este enrolamento também produzirá e será suscetível a um campo E no plano do indutor.as figuras 4-6 mostram diferentes maneiras de neutralizar a corrente circunferencial. A figura 4 é a mais simples e tem a vantagem de que o fio de retorno pode ser adicionado após o indutor ser comprado ou construído.

Fig. 4. Corrente circunferencial contrabalançada com um fio de retorno. O fio é branco e corre entre a borda exterior do indutor e a parte exterior do enrolamento.

Fig. 5. Corrente circunferencial contrabalançada com um enrolamento de retorno.

Fig. 6. Corrente circunferencial contrabalançada com um enrolamento de retorno dividido.

E field in the plane of the toroidEdit

Fig. 7. Simple toroid and the E-field produced. ±100 Volt excitation assumed.

Fig. 8. Voltage distribution with return winding. ±100 Volt excitation assumed.

Haverá uma distribuição de potencial ao longo do enrolamento. Isto pode levar a um campo E no plano do toróide e também a uma susceptibilidade a um campo E no plano do toróide, como mostrado na Figura 7. Isto pode ser mitigado utilizando um enrolamento de Retorno Como mostrado na figura 8. Com este enrolamento, cada lugar onde o enrolamento se cruza, as duas partes estarão em polaridade igual e oposta, o que reduz substancialmente o campo E gerado no plano.

indutor Toroidal/transformador e magnético vetorial potentialEdit

Mostrando o desenvolvimento do vetor potencial magnético em torno de um simétrica indutor toroidal.

ver os capítulos 14 e 15 de Feynman para uma discussão geral do potencial vetor magnético. Veja a página 15-11 de Feynman para um diagrama do potencial do vetor magnético em torno de um solenóide fino que também exibe confinamento interno total do campo B, pelo menos no limite infinito.

O campo é preciso ao usar a suposição b f A = 0 {\displaystyle bf{A}=0}

. Isto seria verdade sob os seguintes pressupostos:

• 1. o gabari de Coulomb é usado
• 2. o calibre de Lorenz é usado e não há distribuição de carga, ρ = 0 {\displaystyle \rho =0\,}
  
• 3. o medidor de Lorenz é usado e a frequência zero é assumida
• 4. o calibre de Lorenz é usado e um zero de freqüência que é baixo o suficiente para negligenciar 1 c 2 ∂ ϕ ∂ t {\displaystyle {\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}}
  

  é assumido.

número 4 será presumido para o resto da presente secção e pode ser referido à”condição quasi-estática”.embora o indutor toroidal axial simétrico, sem corrente circunferencial, confine totalmente o campo B dentro dos enrolamentos, o campo A (potencial vetor magnético) não está confinado. A seta #1 na imagem retrata o potencial vetorial no eixo de simetria. As seções de corrente Radial a e b são distâncias iguais do eixo, mas apontadas em direções opostas, então elas cancelarão. Da mesma forma, os segmentos c E d cancelam. Na verdade, todos os segmentos de corrente radial cancelam. A situação das correntes axiais é diferente. A corrente axial no exterior do toróide é apontada para baixo e a corrente axial no interior do toróide é apontada para cima. Cada segmento de corrente axial no exterior do toróide pode ser combinado com um segmento igual, mas oposto no interior do toróide. Os segmentos no interior são mais próximos do que os segmentos no exterior do eixo, portanto há um componente ascendente líquido do campo A ao longo do eixo de simetria.

Representa o vetor potencial magnético (Um), do fluxo magnético (B) e densidade de corrente (j) campos em torno de um indutor toroidal de secção circular. Linhas mais grossas indicam linhas de campo de maior intensidade média. Círculos na seção transversal do núcleo representam fluxo B saindo da imagem. Mais os sinais na outra secção do núcleo representam fluxo B a entrar na imagem. Div a = 0 foi assumido.

Since the equations ∇ × A = B {\displaystyle \nabla \times \mathbf {A} =\mathbf {B} \ }

, and ∇ × B = μ 0 j {\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} \ }

(assuming quasi-static conditions, i.e. ∂ E ∂ t → 0 {\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0}

) têm a mesma forma, as linhas e os contornos de Uma relacionam B, como as linhas e os contornos de B se relacionam com j. Assim, uma representação de Um campo em torno de um loop de B fluxo (como deve ser produzido em um indutor toroidal) é qualitativamente o mesmo que o campo B em torno de um loop de corrente. A figura à esquerda é uma representação do artista do campo A em torno de um indutor toroidal. As linhas mais grossas indicam caminhos de maior intensidade média (caminhos mais curtos têm maior intensidade de modo que a integral do caminho é a mesma). As linhas são desenhadas apenas para parecer bom e transmitir o olhar geral do campo A.

a acção do transformador Toroidal na presença do confinamento total do campo B

os campos e E E B podem ser calculados a partir dos Campos a e ϕ {\displaystyle \phi \,}

(potencial eléctrico escalar) campos B = ∇ × A. {\displaystyle \mathbf {B} =\nabla \times \mathbf {a} .}

e : E = − ∇ φ − ∂ A ∂ t {\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}

e assim, mesmo que a região fora dos enrolamentos é desprovido de campo B, ele é preenchido com zero E o campo. A quantidade ∂ Um ∂ t {\displaystyle {\frac {\partial \mathbf {A} }{\partial t}}}

é responsável pela desejável campo magnético de acoplamento entre o primário e o secundário, enquanto a quantidade ∇ ϕ {\displaystyle \nabla \phi,\,}

é responsável pela indesejáveis campo elétrico acoplamento entre o primário e o secundário. Os designers do transformador tentam minimizar o acoplamento do campo elétrico. Para o resto desta secção, o ∇ ϕ {\displaystyle \ nabla \ phi\,}

assumirá ser zero, a menos que especificado de outra forma. o teorema de Stokes aplica-se, de modo que a integral do caminho de A é igual ao fluxo B fechado, assim como a integral do caminho B é igual a um tempo constante a Corrente fechada

a integral do caminho de E ao longo do enrolamento secundário dá ao EMF induzido do secundário (força Electro-motriz).

E M F = ∮ p a t h E ⋅ d l = − ∮ p a t h ∂ A ∂ t ⋅ d l = − ∂ ∂ t ∮ p a t h A ⋅ d l = − ∂ ∂ t ∫ s u r f a c e B ⋅ d s {\displaystyle \mathbf {EMF} =\oint _{path}\mathbf {E} \cdot {\rm {d}}l=-\oint _{path}{\frac {\partial \mathbf {A} }{\partial t}}\cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\oint _{path}\mathbf {A} \cdot {\rm {d}}l=-{\frac {\partial }{\partial t}}\int _{surface}\mathbf {B} \cdot {\rm {d}}s}

o que diz o EMF é igual ao tempo taxa de variação de B fluxo entre o enrolamento, que é o resultado normal.

transformador Toroidal vetor de Poynting afastamento do primário para o secundário na presença de total B do campo confinementEdit

nesta figura, os pontos azuis indicam onde B o fluxo de corrente primária vem de fora do quadro e sinais de adição indicar onde ele vai para a imagem.esta figura mostra a metade de um transformador toroidal. Condições quase estáticas são assumidas, então a fase de cada campo é sempre a mesma. O transformador, seus enrolamentos e todas as coisas são distribuídos simetricamente sobre o eixo de simetria. Os enrolamentos são tais que não há corrente circumferencial. Os requisitos são cumpridos para o confinamento interno completo do campo B devido à corrente primária. O núcleo e o enrolamento primário são representados pelo Toro cinza-marrom. O enrolamento primário não é mostrado, mas a corrente no enrolamento na superfície da seção transversal é mostrado como elipses de ouro (ou laranja). O campo B causado pela corrente primária está inteiramente confinado à região delimitada pelo enrolamento primário (ou seja, o núcleo). Pontos azuis na secção transversal da mão esquerda indicam que as linhas de fluxo B no núcleo saem da secção transversal da mão esquerda. Na outra secção, Os sinais azuis mais indicam que o fluxo B entra lá. O campo E proveniente das correntes primárias é mostrado como elipses verdes. O enrolamento secundário é mostrado como uma linha marrom que desce diretamente pelo eixo de simetria. Na prática normal, as duas extremidades do secundário são conectados com um cabo comprido que fica bem longe do toro, mas para manter a absoluta simetria axial, o aparelho inteiro, é concebida como sendo perfeitamente dentro de uma esfera condutora, com o secundário fio “aterrado” para dentro da esfera em cada extremidade. O secundário é feito de fio de resistência, por isso não há carga separada. O campo E ao longo do secundário causa corrente no secundário (setas amarelas) que causa um campo B em torno do secundário (mostrado como elipses azuis). Este campo b preenche espaço, incluindo dentro do núcleo do transformador, de modo que no final, há um campo b Contínuo Não-zero do primário ao secundário, se o secundário não estiver aberto circuited. O produto cruzado do campo E (proveniente das correntes primárias) e do campo B (proveniente das correntes secundárias) forma o vetor de Poynting que aponta do primário para o secundário.