algoritmii de sortare sunt o combinație incomodă de fundamental necesar și profund controversat. De la ingineri noi care doresc să impresioneze într-un interviu la ingineri mai în vârstă care caută o soluție la o bază de date cu scalare rapidă, există nenumărate factori de luat în considerare. Care este viteza de comparație între două obiecte? Care este timpul de schimb? Cât de mare este baza de date? Ce tip de obiecte conține? Este deja semi-sortat? Rezultatele trebuie să fie stabile?

fiecare dintre aceste întrebări poate scoate argumente în favoarea unui algoritm sau altul. Datele sursă sunt mari și complexe? Cele mai multe limbi implicit la standard, Sortare rapidă cu o sa( n log n) complexitatea timpului. Este mai mic? Inserția sortare face minuni pe cei. Cea mai mare parte sortate? Heck, un fel de bule ar putea lucra aproape pentru asta. Dacă doriți să citiți / vizualizați meritele fiecăruia, consultați această comparație prin toptal.com.

un algoritm de sortare pe care nu îl veți găsi pe acel site, sau aproape oricare altul, este Tim Sort. Acest tip obscur este în prezent unic pentru Python și este utilizat ca algoritm de sortare implicit. Apel array.sort în Python, și Tim sortare este ceea ce se execută. În ciuda acestui fapt, este rar să găsești ingineri care îl cunosc și îl înțeleg pe Tim Sort. Deci: ce este?

Fig 1: Tim Peters, inventatorul Timsort

Tim Sort a fost implementat pentru prima dată în 2002 de Tim Peters pentru utilizare în Python. Se presupune că a venit din înțelegerea faptului că majoritatea algoritmilor de sortare se nasc în sălile de școală și nu sunt concepute pentru utilizarea practică a datelor din lumea reală. Tim Sortare profită de modele comune în date, și utilizează o combinație de sortare îmbinare și sortare inserție, împreună cu unele logica internă pentru a optimiza manipularea datelor la scară largă.

Fig 2: compararea complexității diferiților algoritmi de sortare (prin amabilitateahttp://bigocheatsheet.com/)

de ce Tim sortare?

Privind la figura 2, putem vedea imediat ceva interesant. În cel mai bun caz, Tim Sort depășește Merge Sort și Quick Sort. În cel mai rău caz, rulează la viteză comparabilă Merge Sort și depășește de fapt Quick Sort. Cu alte cuvinte, este neașteptat de rapid.

în ceea ce privește spațiul, Tim Sort este la capătul mai rău al spectrului, dar considerația spațială pentru majoritatea algoritmilor de sortare este destul de rară. O (n) nu este prea dur în cele mai multe cazuri; este demn de remarcat ca o posibilă deficiență, și singurul loc în care sortare rapidă întrece într-adevăr Tim Sortare.

elementul final pe care algoritmii de sortare sunt adesea judecați este stabilitatea. Stabilitatea este conceptul că, atunci când sunt sortate, obiectele de valoare egală își mențin ordinea inițială. Acum, s-ar putea să vă întrebați de ce ne pasă de asta. Articolele au o valoare egală — de ce ne deranjează modul în care sunt comandate?

răspunsul simplu este că stabilitatea contează pentru tipurile stivuite. Adică, mai întâi sortați pe baza unui criteriu, apoi pe baza unui al doilea. Dacă faceți acest lucru într-un algoritm instabil, veți pierde instantaneu orice fiabilitate de la primul fel atunci când executați al doilea. Pentru referință, sortarea rapidă este instabilă, iar sortarea Merge este stabilă.

Tim sortare este, de asemenea, stabil, să nu mai vorbim de Rapid Dacă ușor grea(în comparație cu sortare rapidă numai). În timp ce algoritmii de sortare pot (și ar trebui) să fie judecați pe alte considerente, aceștia sunt cei trei mari.

implementarea în trei etape

sortarea Tim este complexă, chiar și după standardele algoritmice. Implementarea este cel mai bine împărțită în părți.

Căutare binară

primul lucru de care aveți nevoie pentru a implementa o sortare Tim este o metodă de căutare binară. Acest lucru este folosit doar pentru a implementa sortarea inserției dvs. mai târziu.

pentru referință: algoritmi de căutare binari

Sortare inserție& Sortare îmbinare

În al doilea rând, trebuie să sortați introducerea codului și să sortați sortarea. Aceștia sunt algoritmi familiari și ar trebui să fie în buzunarul din spate al majorității inginerilor, dar vom trece în revistă fundamentele modului în care funcționează și de ce sunt valoroase pentru noi aici.

Fig 3: Insertionort (prin amabilitateahttps://www.geeksforgeeks.org/insertion-sort/)

sortare inserție este un algoritm de sortare foarte de bază. Acesta trece prin matrice, și ori de câte ori se confruntă cu un element care este în afara de ordine (strict mai puțin/mai mult decât elementul înainte de a), se mută în poziția corespunzătoare în matrice deja sortate. Sortarea inserției este cunoscută pentru că lucrează foarte repede pe matrice deja sortate, precum și pe matrice mai mici. De fapt, putem vedea din Fig 2 că inserția Sortare are un impresionant cel mai bun caz rula timp de O(n). Păstrați în minte merge mai departe cu Tim Sort: cel mai bun caz pentru sortare inserție este o matrice deja sortate. Ar putea suna prostesc, dar asta va fi relevant.

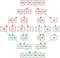
Fig 4: merge sort (prin amabilitateahttps://commons.wikimedia.org/wiki/File:Merge_sort_algorithm_diagram.svg)

Merge Sort pe de altă parte funcționează după un principiu de bază: este extrem de ușor să îmbinați matricele deja sortate. Deci, împarte o matrice de pornire în jumătate de mai multe ori până când nu este altceva decât elemente unice. Apoi reconstruiește încet matricea principală prin îmbinarea acestor elemente înapoi împreună în ordine sortată. Pentru că am pornit de la construirea blocurilor de mărimea unu, a fost foarte ușor să construim matrice sortate inițial. Apoi, este ușor să le îmbinați. În cele din urmă, ne petrecem O(n log n) timp, și (important) facem acest lucru într-un mod care este garantat să fie stabil.

de exemplu implementări vezi:

Merge Sort:https://www.geeksforgeeks.org/merge-sort/

Insertion Sort:https://www.geeksforgeeks.org/insertion-sort/

implementați Tim Sort

cheia înțelegerii implementării Tim Sort este înțelegerea utilizării rulărilor. Tim Sort utilizează datele presortate în mod natural în avantajul său. Prin presortate înțelegem pur și simplu că elementele secvențiale cresc sau scad (Nu ne pasă care).

Mai întâi setăm ominrun Dimensiune. Ceea ce înțelegem prin aceasta este că vrem să ne asigurăm că toate alergările noastre au cel puțin o anumită lungime. Vă rugăm să rețineți că nu garantăm că vom găsi alergări de această dimensiune — vom intra în acest sens mai târziu. Spunem pur și simplu că o alergare trebuie să aibă cel puțin o anumită lungime.

când întâlnim o alergare, o lăsăm deoparte. Când găsim cea mai lungă rulare într-un interval minrun. Acum avem o structură de date familiară: o matrice mică, sortată. Dacă este cel puțin minrun în lungime, atunci huzzah! Putem merge mai departe. Dacă nu este, am pus inserție fel în joc.

s-ar putea să vă amintiți de sus că sortarea inserției este deosebit de eficientă pe două tipuri de matrice: cele mici și cele deja sortate. Ceea ce tocmai am făcut este un mic, matrice sortate. Dacă nu este cel puțin minrun în lungime, ajungem înainte și apucăm suficiente alte elemente pentru a finaliza rularea, apoi folosim sortarea inserției pentru a le împinge în matricea noastră sortată, rapid și ușor. Evident, dacă o alergare întâlnește sfârșitul matricei, o puteți lăsa să fie puțin scurtă.

după ce ați creat toate rulările (adică subarrays sortate), utilizați sortarea de îmbinare pentru a le uni. În cel mai bun caz, întreaga matrice este deja sortată, iar Tim Sort este suficient de inteligent pentru a ști că nu trebuie să facă altceva. Alteori, tinde să fie extrem de eficient. Ca beneficiu suplimentar, atât sortarea inserției, cât și sortarea îmbinării sunt stabile, astfel încât matricea rezultată este stabilă.

pentru cei care preferă gloanțele:

1. stabiliți ominrun dimensiune care este o putere de 2 (de obicei 32, niciodată mai mult de 64 sau sortarea inserției dvs. va pierde eficiența)
2. găsiți o rulare în primulminrun de date.
3. dacă rularea nu este cel puținminrun în lungime, utilizați sortarea inserției pentru a apuca elementele ulterioare sau anterioare și introduceți-le în rulare până când este dimensiunea minimă corectă.
4. repetați până când întreaga matrice este împărțită în subsecțiuni sortate.
5. utilizați a doua jumătate a sortării de îmbinare pentru a vă alătura matricelor ordonate.

concluzie

Tim fel este puternic. Este rapid și stabil, dar poate cel mai important, profită de modelele din lumea reală și le folosește pentru a construi un produs final. Este pentru fiecare situație? Probabil că nu. Mult noroc programarea pe o tablă albă în timpul unui interviu, și dacă aveți nevoie doar de un algoritm rapid de sortare simplu într-un vârf de cuțit, probabil, nu doriți să deranjez de punere în aplicare ceva acest complex. Cu toate acestea, pentru oamenii de știință de date ronțăit numere este mai mult decât merită o privire.

pentru curioși, puteți verifica întregul cod de sortare Tim pe github.

mulțumesc

mulțumesc tuturor cititorilor mei. Apreciez timpul, și sincer sper că ați găsit conținutul informativ. Dacă aveți întrebări sau răspunsuri, nu ezitați să renunțați la una mai jos.