8.2: funcțiile de undă
soluțiile la ecuația atomului de hidrogen Schr sunt funcții care sunt produse ale unei funcții armonice sferice și ale unei funcții radiale.funcțiile de undă pentru atomul de hidrogen depind de cele trei variabile r,\ (\theta\) și \ (\varphi\) și de cele trei numere cuantice n, \(l\) și \ (m_l\). Variabilele dau poziția electronului în raport cu protonul în coordonate sferice. Pătratul absolut al funcției de undă, \(| \psi (r, \theta , \varphi )|^2\), evaluat la \(r\), \(\theta\) și \(\varphi\) dă densitatea probabilității de a găsi electronul în interiorul unui volum diferențial \(d \tau\), centrat în poziția specificată de r, \(\theta\) și \(\varphi\).
Exercise \(\PageIndex{1}\)
care este valoarea integralei
\
numerele cuantice au nume: \(n\) se numește numărul cuantic principal, \(l\) se numește numărul cuantic al momentului unghiular și \(m_l\) se numește numărul cuantic magnetic deoarece (așa cum vom vedea în secțiunea 8.4) energia dintr-un câmp magnetic depinde de \(m_l\). Adesea \(L\) se numește numărul cuantic azimutal, deoarece este o consecință a \(\theta\)-ecuație, care implică unghiul azimutal \(\Theta\), referindu-se la unghiul la zenit.
aceste numere cuantice au valori specifice care sunt dictate de constrângerile fizice sau de condițiile limită impuse ecuației Schr: \(n\) trebuie să fie un număr întreg mai mare de 0, \(l\) poate avea valorile de la 0 la n‑1 și \(m_l\) poate avea \(2L + 1\) valori variind de la \(- l\) ‑ la \(+l\) în pași unitari sau întregi. Valorile numărului cuantic \(l\) sunt de obicei codificate printr-o literă: S înseamnă 0, P înseamnă 1, d înseamnă 2, f înseamnă 3; următoarele coduri continuă alfabetic (de exemplu, G înseamnă \(l = 4\)). Numerele cuantice specifică cuantificarea cantităților fizice. Energiile discrete ale diferitelor stări ale atomului de hidrogen sunt date de \(n\), magnitudinea momentului unghiular este dată de \(l\), iar o componentă a momentului unghiular (de obicei aleasă de chimiști pentru a fi componenta z) este dată de \(m_l\). Numărul total de orbitali cu o anumită valoare de \(n\) este \(N^2\).
Exercise \(\PageIndex{2}\)
luați în considerare mai multe valori pentru n și arătați că numărul de orbitali pentru fiecare N este \(N^2\).
Exercise \(\PageIndex{3}\)
construiți un tabel care rezumă valorile permise pentru numerele cuantice n, \(l\) și \(m_l\). pentru nivelurile de energie de la 1 la 7 de hidrogen.
Exercise \(\PageIndex{4}\)
notația 3d specifică numerele cuantice pentru un electron din atomul de hidrogen. Care sunt valorile pentru n și \(l\) ? Care sunt valorile pentru energie și momentul unghiular? Care sunt valorile posibile pentru numărul cuantic magnetic? Care sunt orientările posibile pentru vectorul momentului unghiular?funcțiile de undă ale atomului de hidrogen, \ (\psi (r , \theta, \ varphi)\), se numesc orbitali atomici. Un orbital atomic este o funcție care descrie un electron într-un atom. Funcția de undă cu n = 1, \(L=1\) și \(m_l\) = 0 se numește orbitalul 1s, iar un electron care este descris de această funcție se spune că este „în” orbitalul ls, adică au o stare orbitală 1s. Constrângerile pe \(n\), \(l)\) și \(m_l\) care sunt impuse în timpul soluției atomului de hidrogen ecuația Schr Xvdinger explică de ce există un singur orbital 1S, de ce există trei orbitali 2p, cinci orbitali 3d etc. Vom vedea când vom lua în considerare atomii multi-electroni în Capitolul 9 că aceste constrângeri explică caracteristicile tabelului Periodic. Cu alte cuvinte, tabelul Periodic este o manifestare a modelului Schr Xvdinger și a constrângerilor fizice impuse pentru a obține soluțiile ecuației Schr Xvdinger pentru atomul de hidrogen.
vizualizarea variației unei funcții de undă electronice cu \(r\), \(\theta\) și \(\varphi\) este importantă deoarece pătratul absolut al funcției de undă descrie distribuția sarcinii (densitatea probabilității electronilor) într-un atom sau moleculă. Distribuția sarcinii este esențială pentru chimie, deoarece este legată de reactivitatea chimică. De exemplu, o parte deficitară de electroni a unei molecule este atrasă de o regiune bogată în electroni a altei molecule, iar astfel de interacțiuni joacă un rol major în interacțiunile chimice, de la reacțiile de substituție și adăugare la plierea proteinelor și interacțiunea substraturilor cu enzimele.
vizualizarea funcțiilor de undă și a distribuțiilor de sarcină este o provocare, deoarece necesită examinarea comportamentului unei funcții de trei variabile în spațiul tridimensional. Această vizualizare este facilitată prin luarea în considerare a părților radiale și unghiulare separat, dar trasarea părților radiale și unghiulare separat nu dezvăluie foarte bine forma unui orbital. Forma poate fi dezvăluită mai bine într-un complot de densitate de probabilitate. Pentru a face un astfel de complot tridimensional, împărțiți spațiul în elemente de volum mic, calculați \(\psi^* \psi \) în centrul fiecărui element de volum și apoi umbriți, stipple sau colorați acel element de volum proporțional cu magnitudinea \(\psi^* \psi \). Nu confundați astfel de parcele cu parcele polare, care arată similar.
densitățile de probabilitate pot fi reprezentate și prin hărți de contur, așa cum se arată în figura \(\PageIndex{1}\).
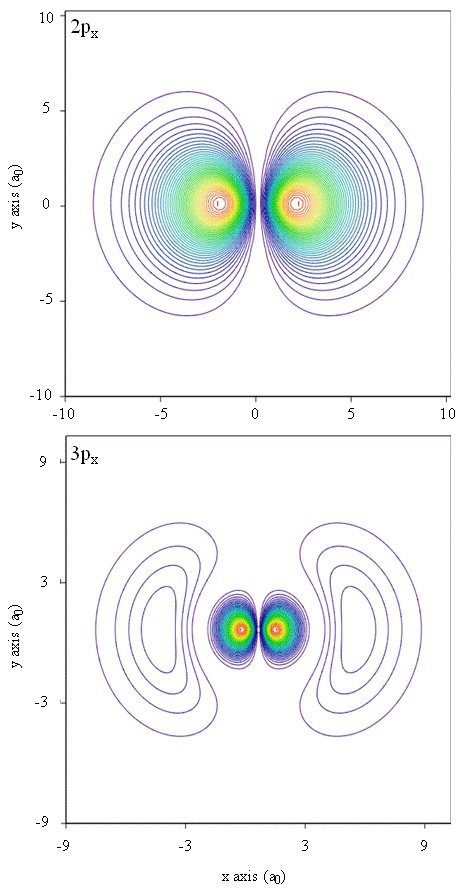
o altă tehnică de reprezentare, modelarea realității virtuale, deține o mare promisiune pentru reprezentarea densităților electronilor. Imaginați-vă, de exemplu, posibilitatea de a experimenta densitatea electronilor ca o forță sau rezistență pe o baghetă pe care o deplasați prin spațiul tridimensional. Dispozitive precum acestea, numite dispozitive haptice, există deja și sunt utilizate pentru a reprezenta informații științifice. În mod similar, nu ar fi interesant să „zburați” printr-un orbital atomic și să experimentați modificări ale densității electronilor pe măsură ce se schimbă culoarea sau se schimbă nebulozitatea? Camerele special concepute cu ecrane 3D și ochelari” inteligenți ” care oferă feedback despre direcția privirii privitorului sunt în prezent dezvoltate pentru a ne permite să experimentăm astfel de senzații.
metodele de examinare separată a porțiunilor radiale ale orbitalilor atomici oferă informații utile despre distribuția densității de încărcare în interiorul orbitalilor. Graficele funcțiilor radiale, \(R (r)\), pentru orbitalele 1s, 2s și 2P reprezentate grafic în figura \(\PageIndex{2}\).
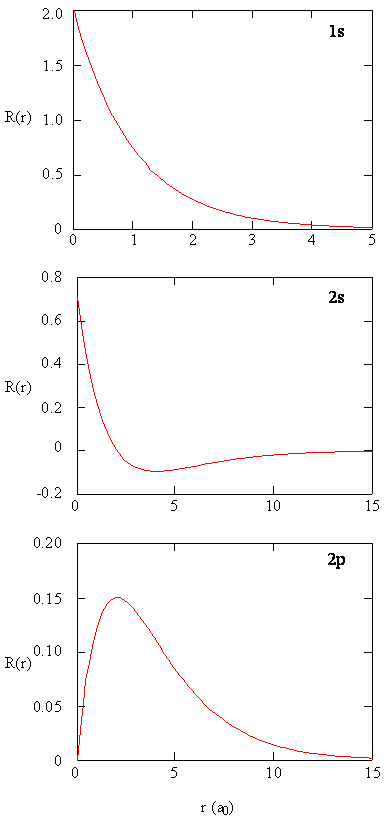
funcția 1s din Figura \(\PageIndex{2}\) începe cu o valoare pozitivă ridicată la nucleu și se descompune exponențial la zero după 5 raze Bohr. Valoarea ridicată a nucleului poate fi surprinzătoare, dar după cum vom vedea mai târziu, probabilitatea de a găsi un electron la nucleu este extrem de mică.
observați cum funcția radială pentru orbitalul 2S, figura \(\PageIndex{2}\), merge la zero și devine negativă. Acest comportament relevă prezența unui nod radial în funcție. Un nod radial are loc atunci când funcția radială este egală cu zero, altul decât at \(r = 0\) sau \(R = 7Q). Nodurile și comportamentele limitative ale funcțiilor orbitale atomice sunt utile în identificarea orbitalului care este descris prin care funcție de undă. De exemplu, toate funcțiile s au valori diferite de zero ale funcției de undă la \(r = 0\), dar p, d, f și toate celelalte funcții merg la zero la origine. Este util să ne amintim că există noduri radiale \(n-1-l\) într-o funcție de undă, ceea ce înseamnă că un orbital 1s nu are noduri radiale, un 2s are un nod radial și așa mai departe.
Exercise \(\PageIndex{5}\)
examinați formele matematice ale funcțiilor de undă radiale. Ce caracteristică din funcții face ca unele dintre ele să meargă la zero la origine, în timp ce funcțiile s nu merg la zero la origine?
Exercise \(\PageIndex{6}\)
Ce caracteristică matematică a fiecărei funcții radiale controlează numărul de noduri radiale?
exercițiu \(\PageIndex{7}\)
la ce valoare a lui r apare nodul radial 2S?
Exercise \(\PageIndex{8}\)
faceți un tabel care furnizează energia, numărul de noduri radiale și numărul de noduri unghiulare și numărul total de noduri pentru fiecare funcție cu n = 1, 2 și 3. Identificați relația dintre energie și numărul de noduri. Identificați relația dintre numărul de noduri radiale și numărul de noduri unghiulare.
cantitatea \(R (r) ^* R(r)\) dă densitatea radială de probabilitate; adică densitatea de probabilitate pentru electron să fie într-un punct situat la distanța \(r\) de proton. Densitățile de probabilitate radială pentru trei tipuri de orbitali atomici sunt reprezentate grafic în figura (\PageIndex{3}\).
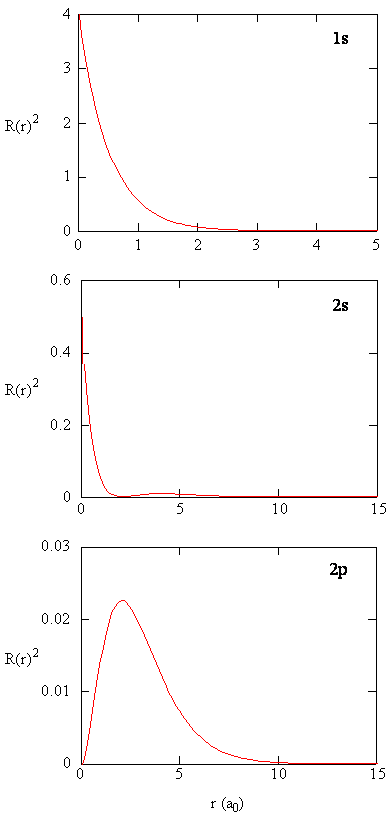
când densitatea de probabilitate radială pentru fiecare valoare a lui r este înmulțită cu aria suprafeței sferice reprezentată de acea valoare particulară a lui r, obținem funcția de distribuție radială. Funcția de distribuție radială dă densitatea de probabilitate ca un electron să fie găsit oriunde pe suprafața unei sfere situate la o distanță r de proton. Deoarece aria unei suprafețe sferice este \(4 \ pi r^2\), funcția de distribuție radială este dată de \(4\pi r^2 R(r) ^* R(r)\).
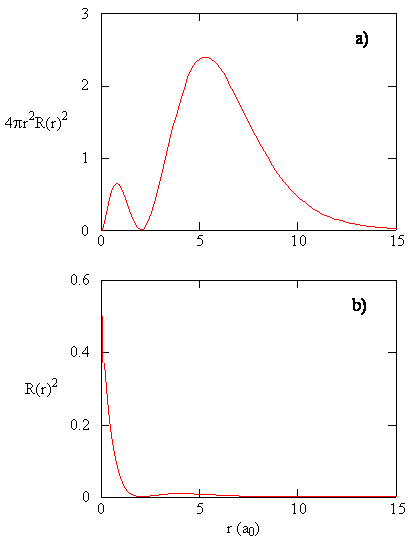
funcțiile de distribuție radială sunt prezentate în figura \(\PageIndex{4}\). La valori mici ale r, funcția de distribuție radială este scăzută, deoarece suprafața mică pentru raze mici modulează valoarea ridicată a funcției de densitate a probabilității radiale în apropierea nucleului. Pe măsură ce creștem \(r\), suprafața asociată cu o valoare dată a lui R crește, iar termenul \(r^2\) determină creșterea funcției de distribuție radială chiar dacă densitatea radială a probabilității începe să scadă. La valori mari ale \(r\), decăderea exponențială a funcției radiale depășește creșterea cauzată de termenul \(r^2\) și funcția de distribuție radială scade.
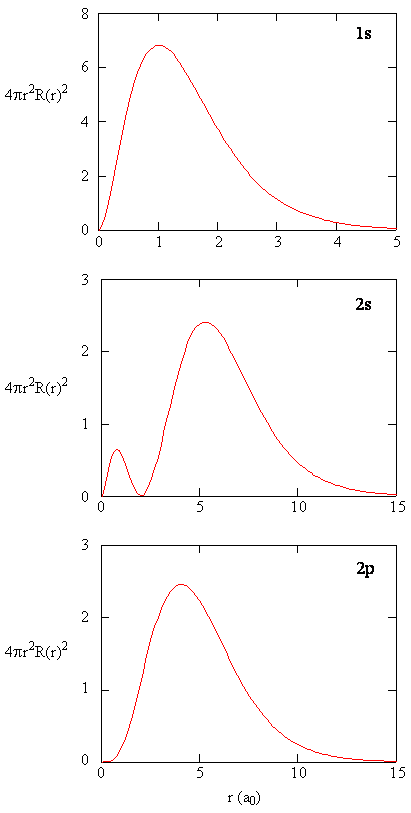
Exercise \(\PageIndex{9}\)
scrieți o comparație de calitate a funcției radiale și a funcției de distribuție radială pentru orbitalul 2S. Vezi figura (\PageIndex{5}\)
colaboratori și atribuții
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski („stări cuantice ale atomilor și moleculelor”)